Moving Average (MA) Models

Chapter 6: Lesson 1

Learning Outcomes

Characterize the properties of moving average (MA) models

• Define a moving average (MA) process
• Write an MA(q) model in terms of the backward shift operator
• State the mean and variance of an MA(q) process
• Explain the autocorrelation function of an MA(q) process
• Define an invertible MA process

Fit time series models to data and interpret fitted parameters

• Determine an appropriate MA(q) model to fit to a time series based on the ACF plot
• Fit an MA(q) model to data in R using the arima() function
• Assess model fit by examining residual diagnostic plots
• Interpret the fitted MA coefficients

Preparation

• Read Sections 6.1-6.4

Learning Journal Exchange (10 min)

• Review another student’s journal

• What would you add to your learning journal after reading another student’s?

• What would you recommend the other student add to their learning journal?

• Sign the Learning Journal review sheet for your peer

Class Activity: Introduction to Moving Average (MA) Models (15 min)

Stationary Processes

In previous chapters, we have explored how to identify and remove the trend and seasonal components of a time series. After the trend and seasonal component have been properly removed, the residual should be stationary. However, these residual components may still contain autocorrelation.

In this chapter, we will explore stationary models that are appropriate when there are no obvious trends or seasonal elements. Combining the fitted stationary model with the estimated trend and seasonal components can improve our ability to make forecasts. We will build on the autoregressive (AR) models we learned in Chapter 4.

Strictly Stationary Series

First, we define a strictly stationary series.

Definition of Strict Stationarity

A time series model \(\{x_t\}\) is said to be strictly stationary if the joint distribution of the random variables \(x_{t_1}, x_{t_2}, \ldots, x_{t_n}\) is the same as the joint distribution of \(x_{t_1+m}, x_{t_2+m}, \ldots, x_{t_n+m}\) for all \(t_1, t_2, \ldots, t_n\) and \(m\), so that the distribution of the values in the time series is the same after an arbitrary time shift.

If a time series is strictly stationary, then its mean and variance are constant in time. Hence, the autocovariance \(cov(x_t, x_s)\) depends only on the lag, \(k = | t - s |\). We can therefore denote the covariance function as \(\gamma(k) = cov(x_t, x_{t+k})\).

Note: It is possible that a series could have a constant mean and variance in time and the autocovariance depends only on the lag, but the series is not strictly stationary. This is called second-order stationary.

We will focus on the second-order properties of the time series, even though all the series we will explore in this chapter are strictly stationary.

Note: if a white noise process is Gaussian, the stochastic process is completely determined by the mean and covariance structure. This is similar to how a (univariate or multivariate) normal distribution is completely specified by the mean and variance-covariance matrix.

The concept of stationarity is a property of time series models. When we use certain models, we are assuming stationarity. Before we apply these models, it is important to check for stationarity in the time series. In other words, we check to see if there is evidence of a trend or seasonality and if so, we remove these components. We can use methods such as decomposition, Holt-Winters, or regression to remove the trend and seasonality. Hence, it is typically reasonable to consider the residual series as a stationary series. Typically the models in this chapter are applied to the residual series from a regression or similar analysis.

Moving Average (MA) Models

Recall in Chapter 4, Lesson 3, we learned the definition of an AR model:

Definition of an Autoregressive (AR) Model

The time series \(\{x_t\}\) is an autoregressive process of order \(p\), denoted as \(AR(p)\), if \[ x_t = \alpha_1 x_{t-1} + \alpha_2 x_{t-2} + \alpha_3 x_{t-3} + \cdots + \alpha_{p-1} x_{t-(p-1)} + \alpha_p x_{t-p} + w_t ~~~~~~~~~~~~~~~~~~~~~~~ (4.15) \]

where \(\{w_t\}\) is white noise and the \(\alpha_i\) are the model parameters with \(\alpha_p \ne 0\).

The \(AR(p)\) model can be expressed in terms of the backward shift operator: \[ \left( 1 - \alpha_1 \mathbf{B} - \alpha_2 \mathbf{B}^2 - \cdots - \alpha_p \mathbf{B}^p \right) x_t = w_t \]

Now, we consider a different, but related model, the moving average (MA) model

Definition of a Moving Average (MA) Model

We say that a time series \(\{x_t\}\) is a moving average process of order \(q\), denoted as \(MA(q)\), if each term in the time series is a linear combination of the current white noise term and the \(q\) most recent past white noise terms.

It is given as: \[ x_t = w_t + \beta_1 w_{t-1} + \beta_2 w_{t-2} + \beta_3 w_{t-3} + \cdots + \beta_{q-1} w_{t-(q-1)} + \beta_q w_{t-q} ~~~~~~~~~~~~~~~~~~~~~~~ (6.1) \]

where \(\{w_t\}\) is white noise with zero mean and variance \(\sigma_w^2\), and the \(\beta_i\) are the model parameters with \(\beta_q \ne 0\).

Check Your Understanding

• Write Equation (6.1) in terms of the backward shift operator. Your answer will be of the form:

\[ x_t = (\text{some}~q^{th}~\text{degree polynomial in}~\mathbf{B}) w_t = \phi_q(\mathbf{B}) w_t \]

Note

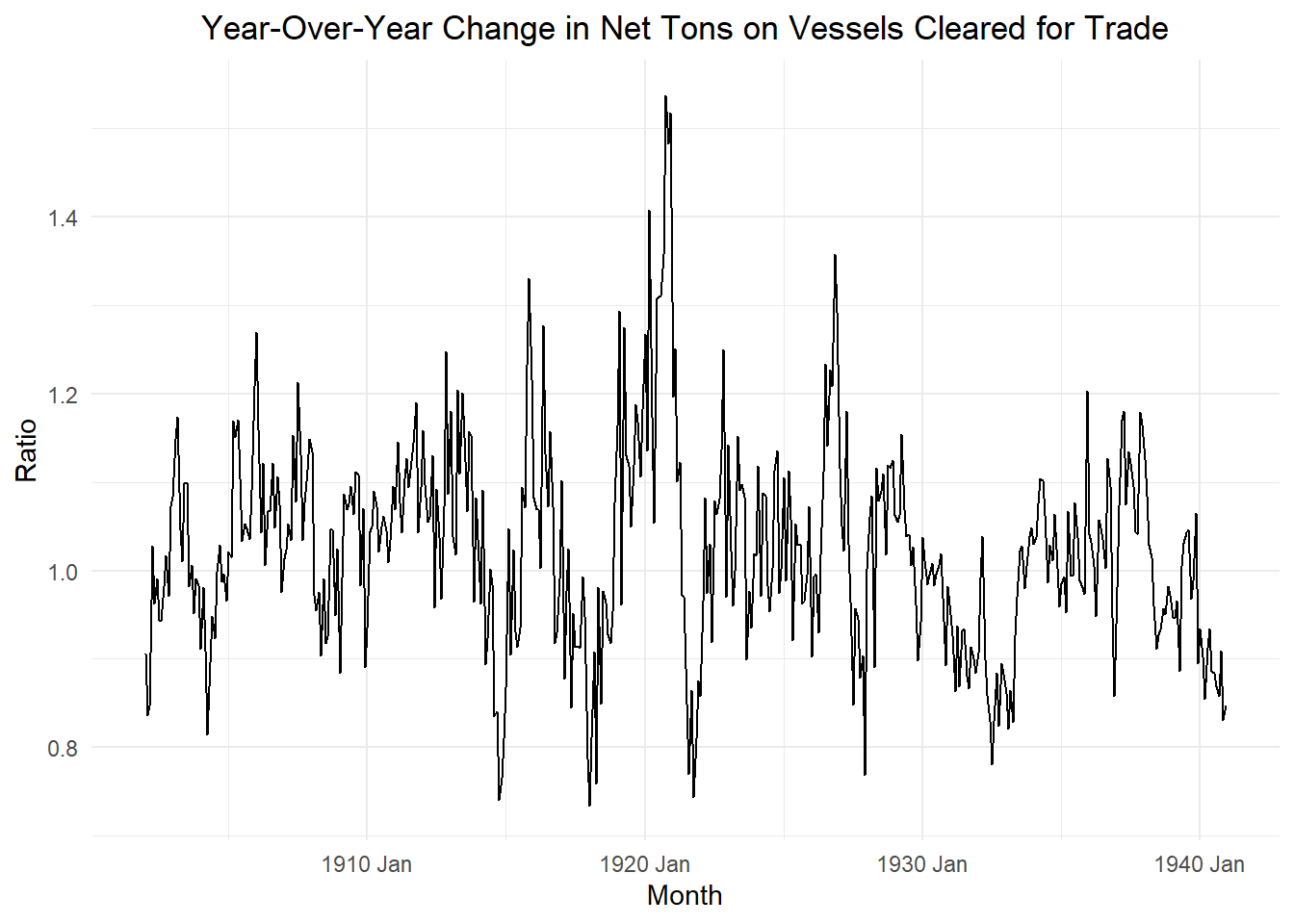
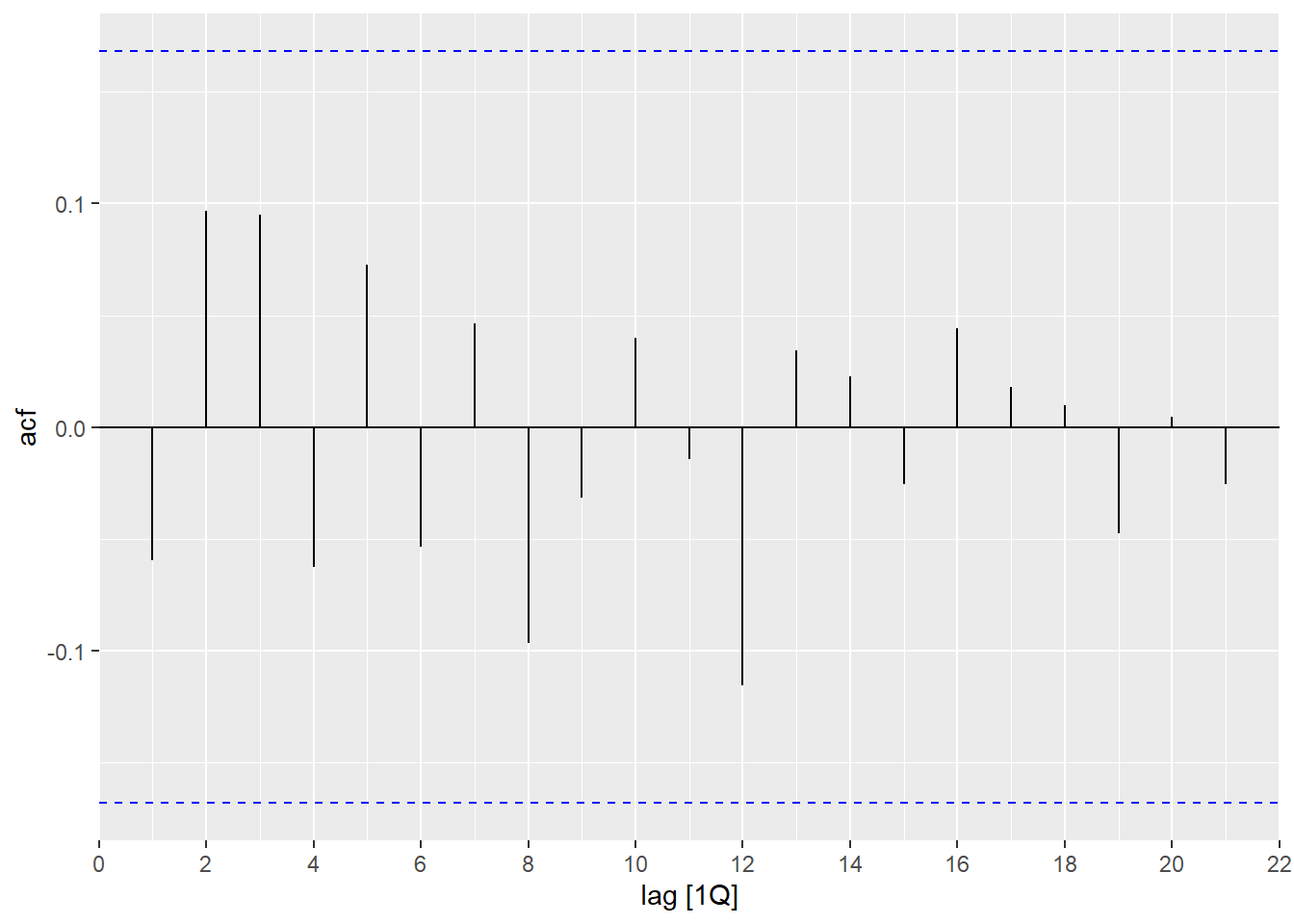
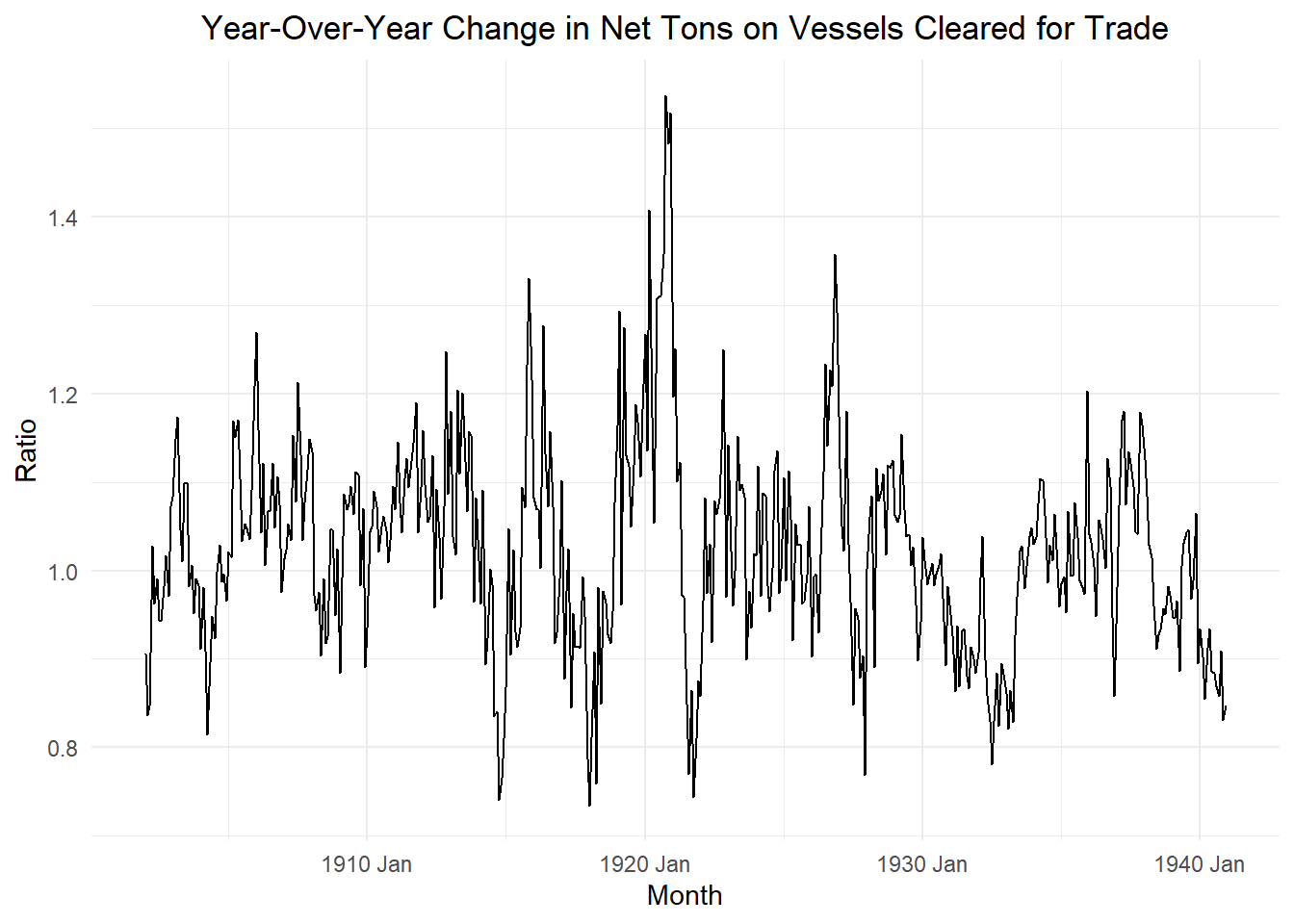
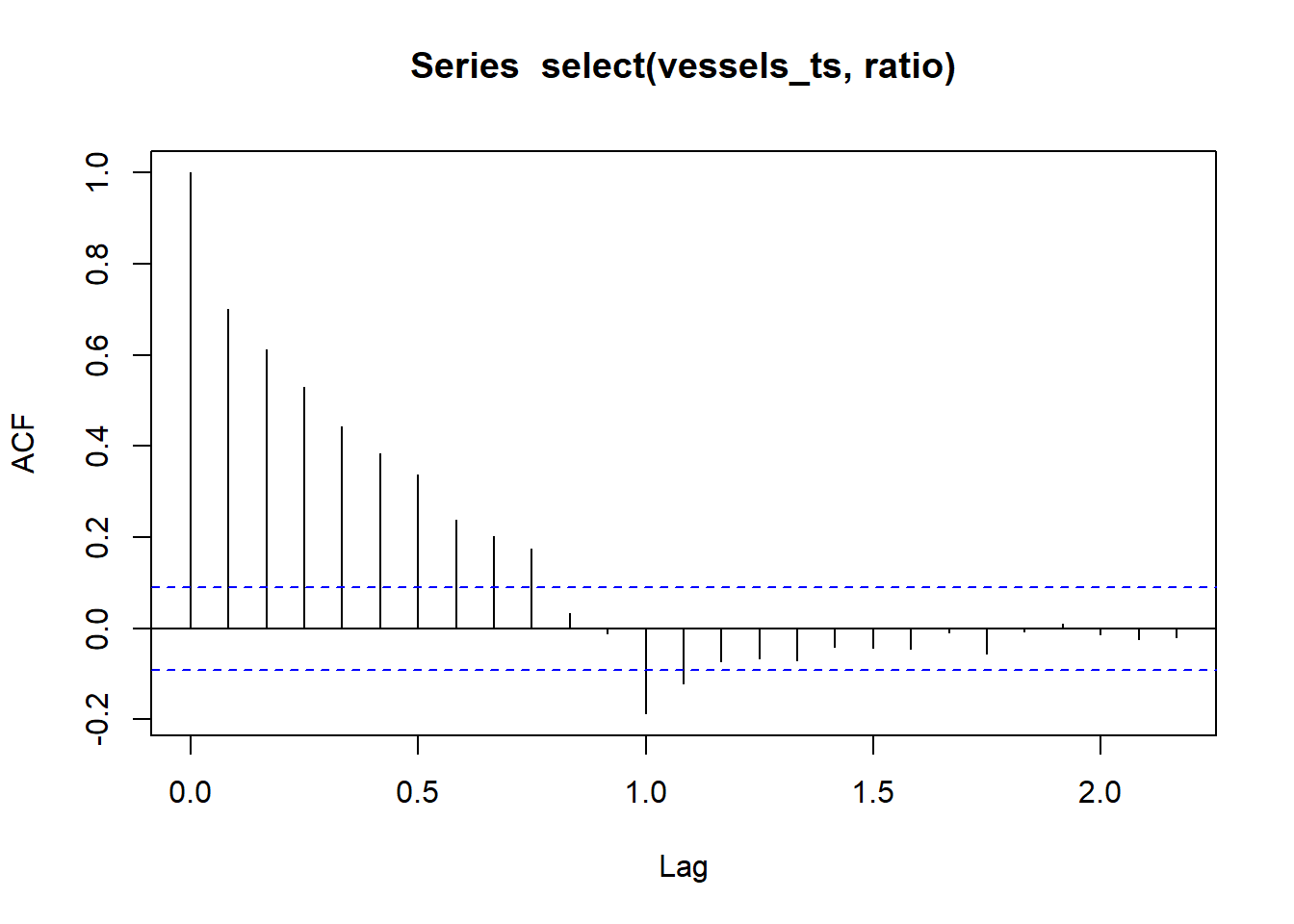
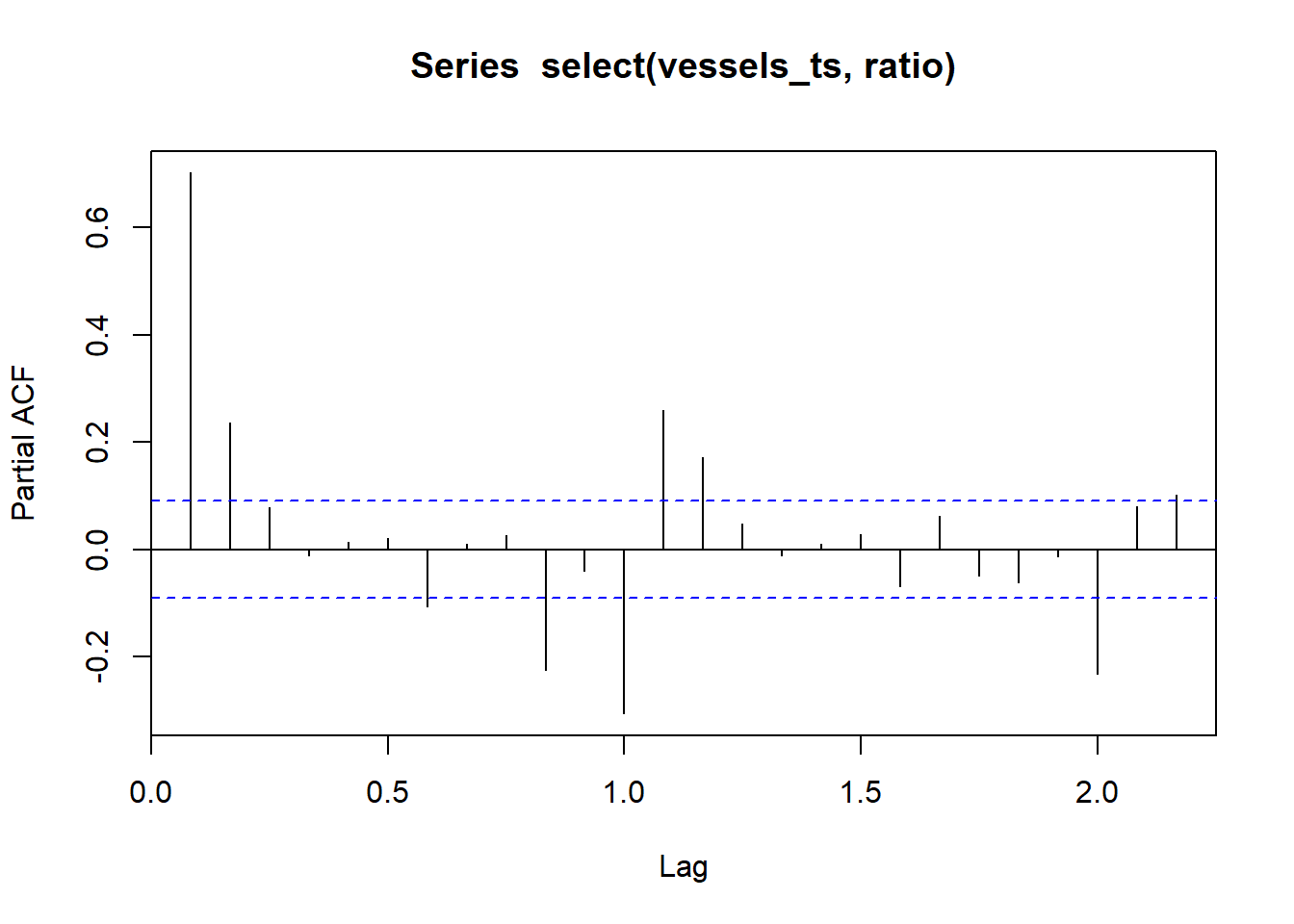
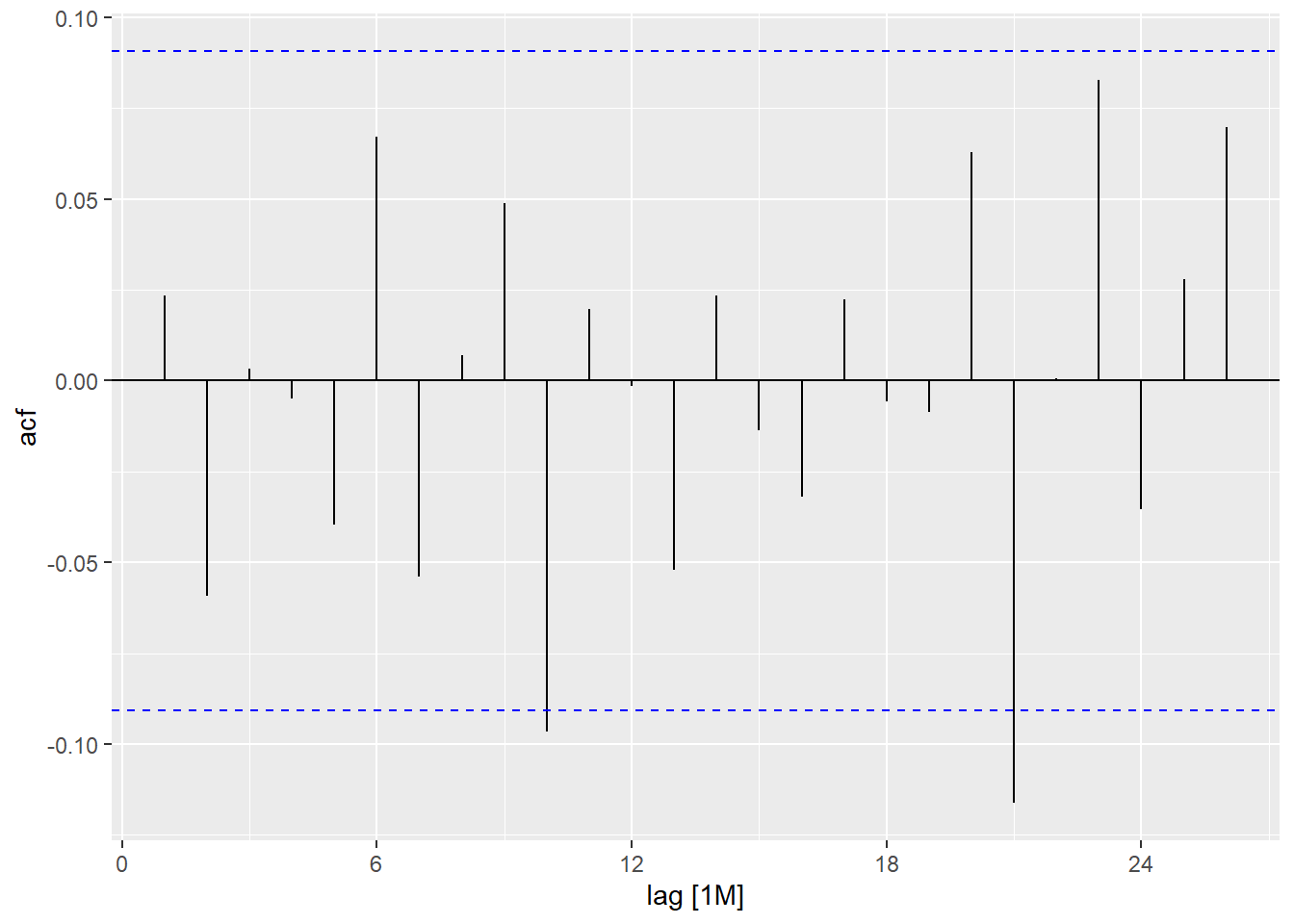
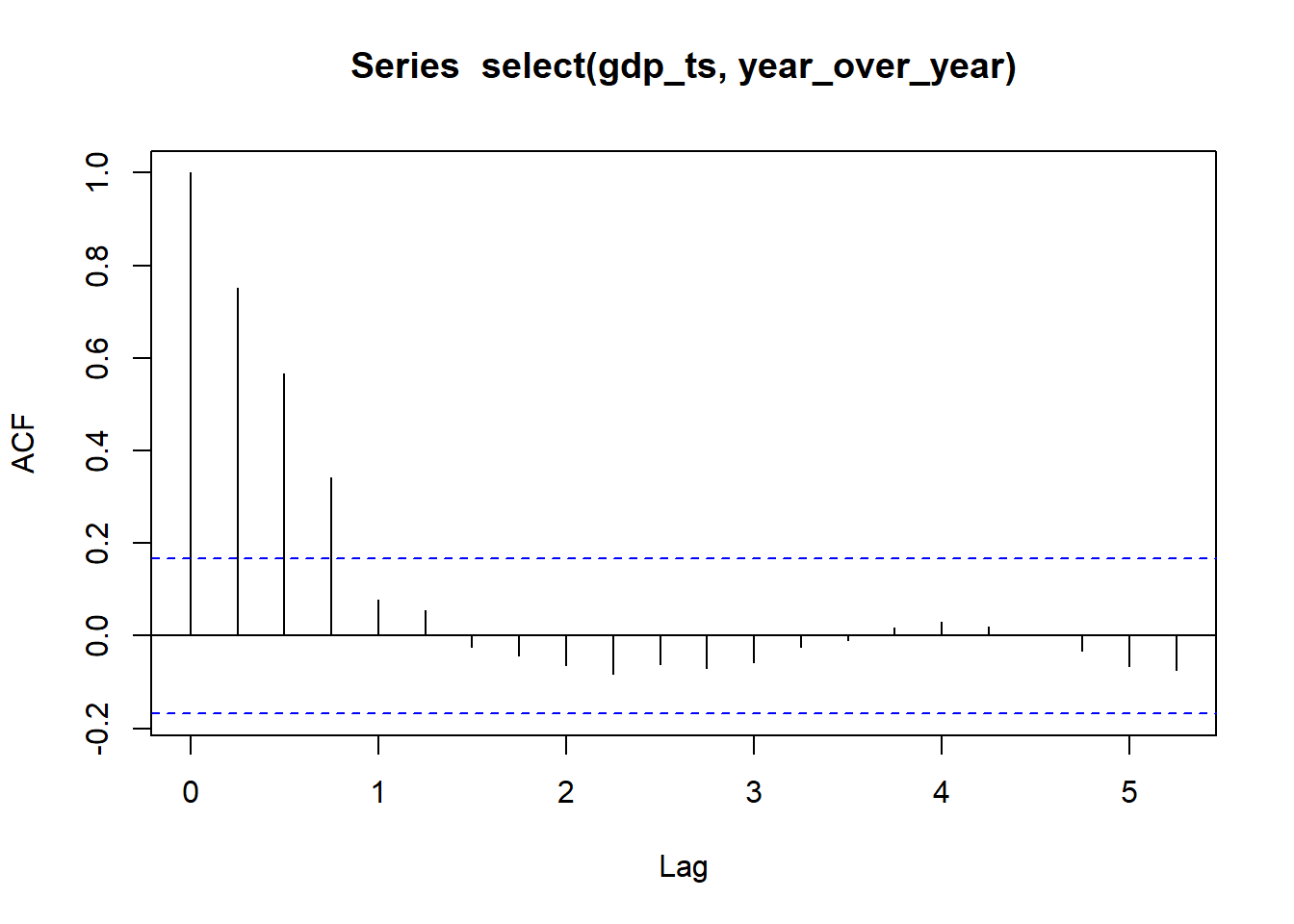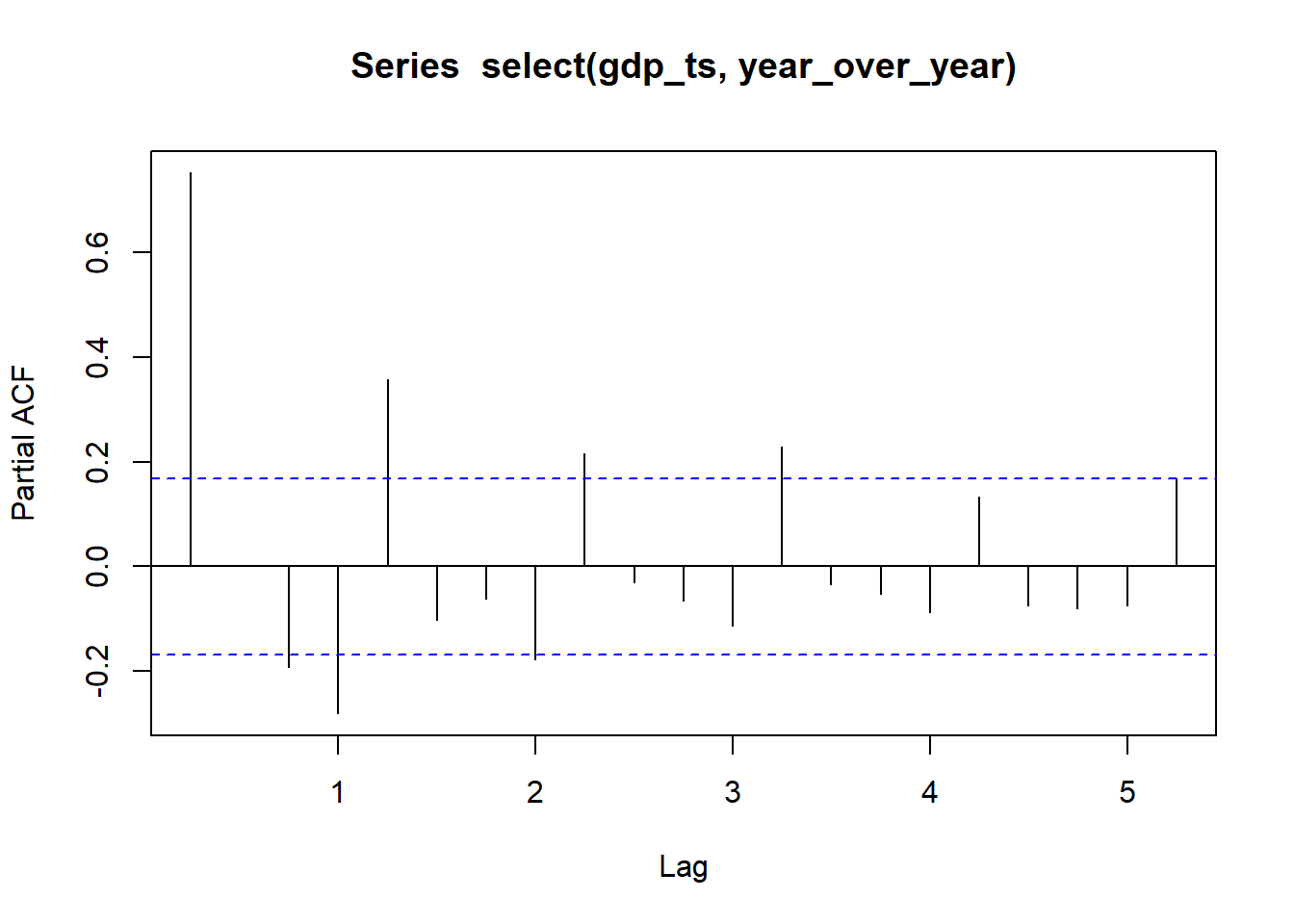An \(MA(q)\) process is comprised of a finite summation of stationary white noise terms. Hence, an \(MA(q)\) process will be stationary with a time-invariante mean and autocovariance.

The mean and variance of \(\{x_t\}\) are easily derived. The mean must be zero, because each term is a sum of scaled white noise terms with mean zero.

The variance of an \(MA(q)\) process is \({ \sigma_w^2 \left( 1 + \beta_1^2 + \beta_2^2 + \beta_3^2 + \cdots + \beta_{q-1}^2 + \beta_q^2 \right) }\). This can be seen, because the white noise terms are independent with the same variance.

So, the autocorrelation function is

\[ \rho(k) = cor(x_t, x_{t+k}) = \begin{cases} 1, & k=0 \\ ~\\ \dfrac{ \sum\limits_{i=0}^{q-k} \beta_i \beta_{i+k} }{ \sum\limits_{i=0}^q \beta_i^2 }, & k = 1, 2, \ldots, q \\ ~\\ 0, & k > q \end{cases} \] where \(\beta_0 = 1\).

Note that the autocorrelation function is zero if \(k>q\), because \(x_t\) and \(x_{t+k}\) would be independent weighted summations of white noise processes and hence the covariance between them would be zero.

We now define an invertible \(MA\) process.

Definition of an Invertible \(MA\) Process

An \(MA\) process is said to be invertible if it can be expressed as a stationary autoregressive process (of infinite order) with no error term.

Example of an Invertible MA Process

Recall that \[ (1-x)(1 + x + x^2 + x^3 + \cdots) = 1 \]

or,

\[ (1-x)^{-1} = (1 + x + x^2 + x^3 + \cdots) \] if \(|x|<1\).

Now, note that the \(MA\) process

\[ x_t = \left( 1 - \beta \mathbf{B} \right) w_t \]

can be written as:

\[\begin{align*} \left( 1 - \beta \mathbf{B} \right)^{-1} x_t &= w_t \\ \left( 1 + \beta \mathbf{B} + \beta^2 \mathbf{B}^2 + \beta^3 \mathbf{B}^3 + \cdots \right) x_t &= w_t \\ x_t + \beta x_{t-1} + \beta^2 x_{t-2} + \beta^3 x_{t-3} + \cdots &= w_t \\ x_t &= \left( -\beta x_{t-1} - \beta^2 x_{t-2} - \beta^3 x_{t-3} - \cdots \right) + w_t \end{align*}\]

assuming that \(|\beta|<1\). Note that this series will not converge unless \(|\beta|<1\).

We have just shown that the \(MA\) process \[ x_t = \left( 1 - \beta \mathbf{B} \right) w_t \] is invertible.

Theorem: Invertibility of an \(MA(q)\) Process

The \(MA(q)\) process \[ x_t = \phi_q(\mathbf{B}) w_t \] will be invertible if the solutions to the equation \[ \phi_q(\mathbf{B}) = 0 \] are all greater than 1 in absolute value.

Does this remind you of the test for the stationarity of an \(AR(p)\) model?

Note that the autocovariance function (acvf) will identify a unique \(MA(q)\) process only if the process is invertible. Fortunately, the algorithm R uses to estimate an \(MA(q)\) process always leads to an invertible model.

Class Activity: Simulating an \(MA(q)\) Model (5 min)

The textbook gives a simulation of an \(MA(3)\) process:

\[ x_t = w_t + \beta_1 w_{t-1} + \beta_2 w_{t-2} + \beta_3 w_{t-3} \]

where \(\beta_1 = 0.7\), \(\beta_1 = 0.5\), and \(\beta_3 = 0.2\). This shiny app allows you to simulate from this process.

Check Your Understanding

Use the simulation above to do the following:

• Generate the theoretical acf plot for the \(MA(3)\) model \[ x_t = w_t - 0.7 w_{t-1} + 0.5 w_{t-2} - 0.2 w_{t-3} \]
• How does the value of the \(\beta\)’s affect the acf?
• Simulate 1000 observations from this \(MA(3)\) process.
  • Give the time plot of the simulated data
  • Plot the acf of the simulated data.
• Compare the acf from the simulated data with the theoretical acf.

Class Activity: Identifying AR and MA Models from the ACF and PACF (5 min)

AR Process

Recall that on page 81, the textbook states that in general, the partial autocorrelation at lag \(k\) is the \(k^{th}\) coefficient of a fitted \(AR(k)\) model. This implies that if the underlying process is \(AR(p)\), then all the coefficients \(\alpha_k\) will equal 0 whenever \(k>p\). So, an \(AR(p)\) process will result in partial correlations that are zero after lag \(p\). So, we can look at the correlogram of partial autocorrelations to determine the order of an appropriate \(AR\) process to model a time series.

MA Process

Similarly, for an \(MA(q)\) process, the coefficients \(\beta_k\) will equal 0 whenever \(k > q\). Hence, an \(MA(q)\) process will demonstrate autocorrelations that are 0 after lag \(q\). So, considering the correlogram of autocorrelations, we can assess if an \(MA(q)\) model would be appropriate.

Bless their hearts, the textbook authors give a bad example in Section 6.4.2. They even state that it is “not a realistic realisation.” MA processes naturally arise in ratios of observed data. Multi-period asset returns (i.e. ratios of some previous term’s value) tend to follow an MA process.

For example, if there are 252 trading days in a year, then the daily series of year-over-year returns (this year’s value divided by last year’s value) follows an \(MA(252-1)\) process. If we are comparing values observed to those from one week ago, we would have an \(MA(7-1)\) process.

Comparison

ACF and PACF of an \(AR(p)\) Process

We can use the pacf and acf plots to assess if an \(AR(p)\) or \(MA(q)\) model is appropriate. For an \(AR(p)\) or \(MA(q)\) process, we observe the following:

	AR(p)	MA(q)
ACF	Tails off	Cuts off after lag \(q\)
PACF	Cuts off after lag \(p\)	Tails off

Class Activity: Fitting an \(MA(q)\) Model to GDP Year-Over-Year Ratios (5 min)

To fit an \(MA(q)\) model, we look at the acf to determine if it cuts off after \(q\) lags.

# gdp_ts <- rio::import("https://byuistats.github.io/timeseries/data/gdp_fred.csv") |>
gdp_ts <- rio::import("data/gdp_fred.csv") |>
  select(-comments) |>
  mutate(year_over_year = gdp_millions / lag(gdp_millions, 4)) |>
  mutate(quarter = yearquarter(mdy(quarter))) |>
  filter(quarter >= yearquarter(my("Jan 1990")) & quarter < yearquarter(my("Jan 2025"))) |>
  na.omit() |>
  mutate(t = 1:n()) |>
  mutate(std_t = (t - mean(t)) / sd(t)) |>
  as_tsibble(index = quarter)

gdp_ts |>
  autoplot(.vars = gdp_millions) +
    labs(
      x = "Quarter",
      y = "GDP (Millions of $US)",
      title = "U.S. Gross Domestic Product (GDP) in Millions of Dollars"
    ) +
    theme_minimal() +
    theme(plot.title = element_text(hjust = 0.5))

gdp_ts |>
  autoplot(.vars = year_over_year) +
  stat_smooth(method = "lm", 
              formula = y ~ x, 
              geom = "smooth",
              se = FALSE,
              color = "#E69F00",
              linetype = "dotted") +
    labs(
      x = "Quarter",
      y = "Ratio",
      title = "Year-Over-Year Change in U.S. GDP"
    ) +
    theme_minimal() +
    theme(plot.title = element_text(hjust = 0.5))

gdp_ts |>
  select(year_over_year) |>
  acf()

gdp_ts |>
  select(year_over_year) |>
  pacf()

Check Your Understanding

• What process would you use to model the year-over-year GDP ratios?
• Modify the code below to implement your model.

gdp_ma <- gdp_ts |>
  model(arima = ARIMA(year_over_year ~ 1 + pdq(0,0,1) + PDQ(0, 0, 0)))

tidy(gdp_ma)

gdp_ma |>
  residuals() |>
  ACF() |>
  autoplot()

• What are the values of the model coefficients?
• Based on the acf of the residuals, is the MA model you identified a good fit to the data?

Small-Group Activity: Fitting an \(MA(q)\) Model to the Trade Data (15 min)

Vessels Cleared in Foreign Trade for United States

In the homework for Chapter 1 Lesson 5, you explored data on the thousands of net tons cleared in foreign trade for the United States each month from January 1902 to December 1940. The code below computes the year-over-year change in the amount of cargo cleared for trade. This is stored in the variable ratio.

vessels_ts <- rio::import("https://byuistats.github.io/timeseries/data/Vessels_Trade_US.csv") |>
  # filter(-comments) |>
  mutate(
    date = yearmonth(dmy(date)),
    ratio = vessels / lag(vessels, 12)
  ) |>
  na.omit() |>
  as_tsibble(index = date)

vessels_ts |>
  autoplot(.vars = ratio) +
    labs(
      x = "Month",
      y = "Ratio",
      title = "Year-Over-Year Change in Net Tons on Vessels Cleared for Trade"
    ) +
    theme_minimal() +
    theme(plot.title = element_text(hjust = 0.5))

Check Your Understanding

Practice applying an \(MA(q)\) model using the year-over-year amounts.

• Determine which MA model is most appropriate for these data.
• Fit the model you deem most appropriate.
• Assess the appropriateness of applying your model to the data.

Homework Preview (5 min)

• Review upcoming homework assignment
• Clarify questions

Download Homework

homework_6_1.qmd

MA(q) process in terms of the backward shift operator

\[\begin{align*} x_t &= w_t + \beta_1 w_{t-1} + \beta_2 w_{t-2} + \beta_3 w_{t-3} + \cdots + \beta_{q-1} w_{t-(q-1)} + \beta_q w_{t-q} \\ &= w_t + \beta_1 \mathbf{B} w_t + \beta_2 \mathbf{B}^2 w_t + \beta_3 \mathbf{B}^3 w_t + \cdots + \beta_{q-1} \mathbf{B}^{q-1} w_t + \beta_q \mathbf{B}^{q} w_t \\ &= \left( 1 + \beta_1 \mathbf{B} + \beta_2 \mathbf{B}^2 + \beta_3 \mathbf{B}^3 + \cdots + \beta_{q-1} \mathbf{B}^{q-1} + \beta_q \mathbf{B}^{q} \right) w_t \\ &= \phi_q(\mathbf{B}) w_t \end{align*}\]

Simulating an MA(3) process

Set the values of the parameters \(n\), \(\beta_1\), \(\beta_2\), and \(\beta_3\) in the simulation to the following: \[ n = 1000, ~~~~~~~~~~~ \beta_1 = -0.7, ~~~~~~~~~~~ \beta_2 = 0.5, ~~~~~~~~~~~ \beta_3 = -0.2 \]

Class Activity: Fitting an MA(q) Model to GDP Year-Over-Year Ratios

Check Your Understanding

• What process would you use to model the year-over-year GDP ratios?

Based on the acf, an \(MA(3)\) model seems most appropriate.

gdp_ts |>
  select(year_over_year) |>
  acf()

gdp_ts |>
  select(year_over_year) |>
  pacf()

• Modify the code below to implement your model.

gdp_ma <- gdp_ts |>
  # Changed 1 to a 3 on the next line
  model(arima = ARIMA(year_over_year ~ 1 + pdq(0,0,3) + PDQ(0, 0, 0))) 

• What are the values of the model coefficients?

The values of the coefficients are given in the table below:

tidy(gdp_ma)

# A tibble: 4 × 6
  .model term     estimate std.error statistic   p.value
  <chr>  <chr>       <dbl>     <dbl>     <dbl>     <dbl>
1 arima  ma1         0.978   0.0341       28.7 1.32e- 59
2 arima  ma2         1.01    0.0413       24.5 8.75e- 52
3 arima  ma3         0.965   0.0389       24.8 2.32e- 52
4 arima  constant    1.05    0.00435     241.  7.17e-181

• Based on the acf of the residuals, is the MA model you identified a good fit to the data?

gdp_ma |>
  residuals() |>
  ACF(var = .resid) |>
  autoplot()

Warning: The `...` argument of `PACF()` is deprecated as of feasts 0.2.2.
ℹ ACF variables should be passed to the `y` argument. If multiple variables are
  to be used, specify them using `vars(...)`.

None of the acf values are significant. The \(MA(3)\) model seems appropriate.

We can write the estimated model as: \[ x_t = 1.0478741 + 0.9783408 \mathbf{B} + 1.0127334 \mathbf{B}^2 + 0.9651468 \mathbf{B}^3 \]

The absolute values of the roots of the right-hand side of this equation are:

coeffs <- tidy(gdp_ma) |>
  # filter(term != "constant") |>
  select(estimate) |>
  pull()

abs(polyroot(c(coeffs |> tail(1), coeffs |> head(-1))))

[1] 1.012232 1.059633 1.012232

The model is invertible. (As mentioned previously, the process by which these are constructed guarantees they will be invertible.)

Small-Group Activity: Fitting an MA(q) Model to the Trade Data

vessels_ts <- rio::import("https://byuistats.github.io/timeseries/data/Vessels_Trade_US.csv") |>
  # filter(-comments) |>
  mutate(
    date = yearmonth(dmy(date)),
    ratio = vessels / lag(vessels, 12)
  ) |>
  na.omit() |>
  as_tsibble(index = date)

vessels_ts |>
  autoplot(.vars = ratio) +
    labs(
      x = "Month",
      y = "Ratio",
      title = "Year-Over-Year Change in Net Tons on Vessels Cleared for Trade"
    ) +
    theme_minimal() +
    theme(plot.title = element_text(hjust = 0.5))

vessels_ts |>
  select(ratio) |>
  acf()

vessels_ts |>
  select(ratio) |>
  pacf()

gdp_ma <- vessels_ts |>
  model(arima = ARIMA(ratio ~ 1 + pdq(0,0,12) + PDQ(0, 0, 0)))

tidy(gdp_ma)

# A tibble: 13 × 6
   .model term     estimate std.error statistic   p.value
   <chr>  <chr>       <dbl>     <dbl>     <dbl>     <dbl>
 1 arima  ma1         0.572    0.0475     12.0  2.70e- 29
 2 arima  ma2         0.558    0.0475     11.8  4.09e- 28
 3 arima  ma3         0.601    0.0589     10.2  3.55e- 22
 4 arima  ma4         0.488    0.0582      8.38 6.21e- 16
 5 arima  ma5         0.430    0.0585      7.35 8.83e- 13
 6 arima  ma6         0.457    0.0659      6.94 1.27e- 11
 7 arima  ma7         0.323    0.0600      5.37 1.23e-  7
 8 arima  ma8         0.358    0.0558      6.42 3.36e- 10
 9 arima  ma9         0.479    0.0607      7.90 1.98e- 14
10 arima  ma10        0.411    0.0514      7.99 1.04e- 14
11 arima  ma11        0.517    0.0471     11.0  4.69e- 25
12 arima  ma12       -0.306    0.0586     -5.22 2.70e-  7
13 arima  constant    1.02     0.0171     59.8  2.45e-221

gdp_ma |>
  residuals() |>
  ACF() |>
  autoplot()

Response variable not specified, automatically selected `var = .resid`