Additive Models

Chapter 1: Lesson 4

Learning Outcomes

Use R to describe key features of time series data

• Import CSV data and convert to tsibble format

Decompose time series into trends, seasonal variation, and residuals

• Implement additive decomposition
• Explain how to remove seasonal variation using an estimate for seasonal component of a time series
• Compute the estimators of seasonal variation for an additive model
• Calculate the random component for an additive model
• Compute a seasonally-adjusted time series based on an additive model

Preparation

• Read Sections 1.5.4-1.5.5 and 1.6

Learning Journal Exchange (10 min)

• Review another student’s journal
• What would you add to your learning journal after reading your partner’s?
• What would you recommend your partner add to their learning journal?
• Sign the Learning Journal review sheet for your peer

Converting from a Data File to a Tsibble (5 min)

This is a demonstration of two ways to convert an Excel or csv data file to a tsibble.

deaths_df <- rio::import("https://byuistats.github.io/timeseries/data/traffic_deaths.xlsx")

# Method 1: Create date from scratch based on pattern of rows
# This only works if the data are in ascending order with no missing values
# Note: This file is not in the right order, so this code gives the wrong tsibble
# unless you sort the Excel file before proceeding.
start_date <- lubridate::ymd("2017-01-01")
date_seq <- seq(start_date,
                start_date + months(nrow(deaths_df)-1),
                by = "1 months")
deaths_tibble <- tibble(
  dates = date_seq,
  year = lubridate::year(date_seq),
  month = lubridate::month(date_seq),
  value = pull(deaths_df, Deaths)
)

# Method 2: Build using the date information in the Excel file
deaths_tibble <- deaths_df |>
  mutate(
    date_str = paste("1", Month, Year),
    dates = dmy(date_str),
    year = lubridate::year(dates),
    month = lubridate::month(dates),
    value = Deaths
  ) |>
  dplyr::select(dates, year, month, value)  |> 
  tibble()

# Create the index variable and convert to a tsibble
deaths_ts <- deaths_tibble |>
  mutate(index = tsibble::yearmonth(dates)) |>
  as_tsibble(index = index) |>
  dplyr::select(index, dates, year, month, value) |>
  rename(deaths = value) # rename value to emphasize data context

This results in a tsibble. The first few rows are given here:

# A tsibble: 6 x 5 [1M]
     index dates       year month deaths
     <mth> <date>     <dbl> <dbl>  <dbl>
1 2017 Jan 2017-01-01  2017     1   3034
2 2017 Feb 2017-02-01  2017     2   2748
3 2017 Mar 2017-03-01  2017     3   3164
4 2017 Apr 2017-04-01  2017     4   3238
5 2017 May 2017-05-01  2017     5   3416
6 2017 Jun 2017-06-01  2017     6   3492

Data Visualizations (5 min)

The following time plot illustrates the data in this time series.

Time Series Plot

Default y-axis

This is the plot R creates by default

autoplot(deaths_ts, .vars = deaths) +  
  labs(
    x = "Month",
    y = "Traffic Fatalities",
    title = "Traffic Fatalities in the United States (by Month)"
  ) +
  theme(plot.title = element_text(hjust = 0.5))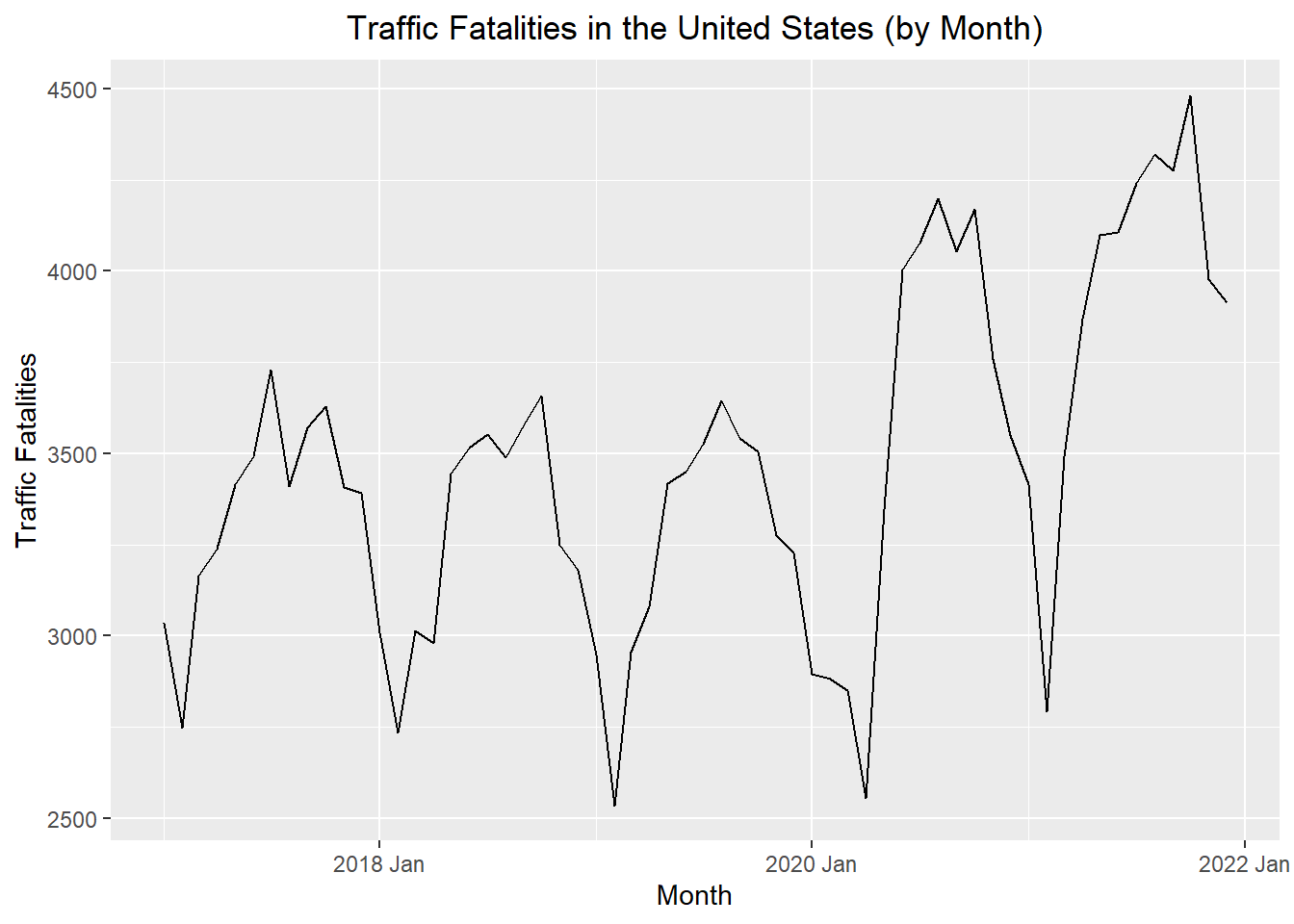

Adjusted y-axis

The vertical axis was adjusted in this plot, so it would begin at 0.

autoplot(deaths_ts, .vars = deaths) +
  labs(
    x = "Month",
    y = "Traffic Fatalities",
    title = "Traffic Fatalities in the United States (by Month)"
  ) +
  coord_cartesian(ylim = c(0, 4500)) +
  theme(plot.title = element_text(hjust = 0.5))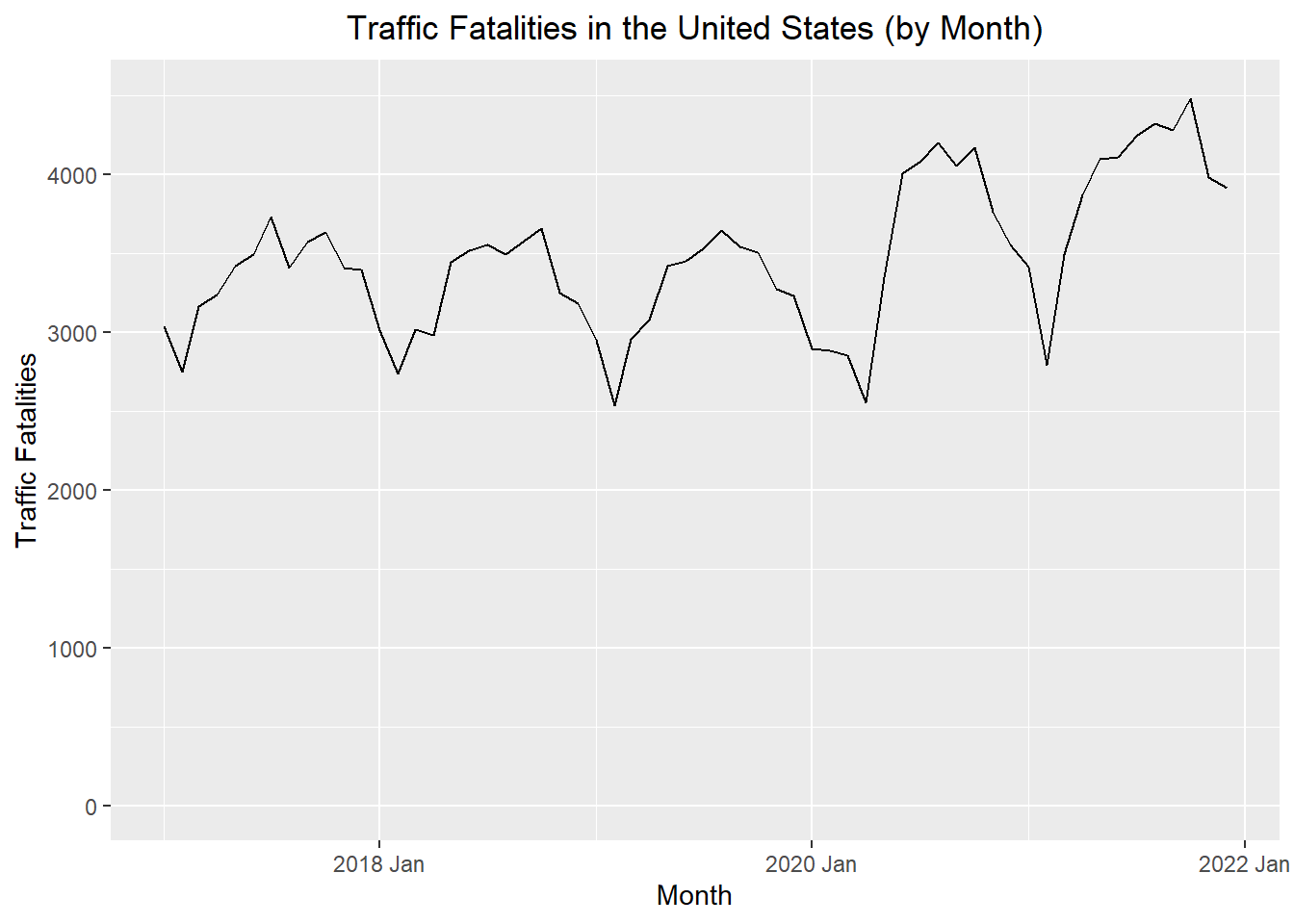

Check Your Understanding

• What do you notice?
  • Does it seem like there is a trend in the time series?
  • Is there evidence of a seasonal effect? If so, when is the number of fatalities particularly high? particularly low?
• Which of the two time plots above is superior? Why?

Visualization of Seasonal Effects: Side-by-Side Box Plots

These side-by-side box plots illustrate the seasonal effect present in the data.

ggplot(deaths_ts, aes(x = factor(month), y = deaths)) +
    geom_boxplot() +
  labs(
    x = "Month Number",
    y = "Deaths",
    title = "Boxplots of Traffic Deaths by Month"
  ) +
  theme(plot.title = element_text(hjust = 0.5))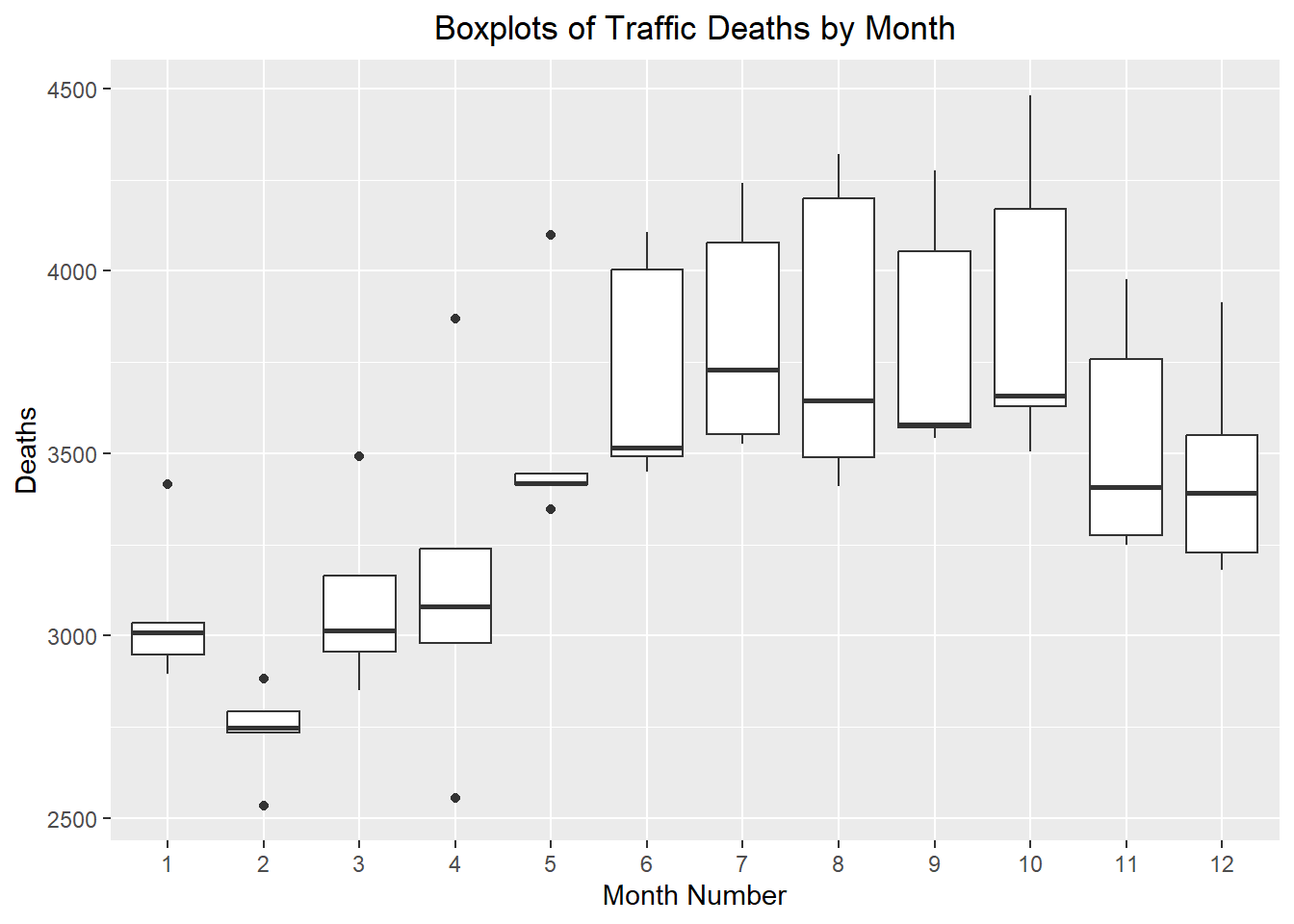

Check Your Understanding

• How do the positions of the box plots correspond to the times of the year where you noted more (or less) deaths occurring?

Computing the Seasonally Adjusted Series (25 min)

Our objective is to find an estimate for the time series that does not fluctuate with the seasons. This is called the seasonally adjusted series.

Centered Moving Average

First, we compute the centered moving average, \(\hat m_t\). This computation was explored in detail in the previous lesson. This code can be used to compute the 12-month centered moving average.

# computes the 12-month centered moving average (m_hat)
deaths_ts <- deaths_ts |> 
  mutate(
    m_hat = (
          (1/2) * lag(deaths, 6)
          + lag(deaths, 5)
          + lag(deaths, 4)
          + lag(deaths, 3)
          + lag(deaths, 2)
          + lag(deaths, 1)
          + deaths
          + lead(deaths, 1)
          + lead(deaths, 2)
          + lead(deaths, 3)
          + lead(deaths, 4)
          + lead(deaths, 5)
          + (1/2) * lead(deaths, 6)
        ) / 12
  )

To emphasize the computation of the centered moving average, the observed data values that were used to find \(\hat m_t\) for December 2017 are shown in green in the table below.

Estimated Monthly Additive Effect

The centered moving average, \(\hat m_t\), is then used to compute the monthly additive effect, \(\hat s_t\):

\[ \hat s_t = x_t - \hat m_t \]

Table 1: Computation of the Centered Moving Average, \(\hat m_t\), and the Estimated Monthly Additive Effect, \(\hat s_t\)

Month	Deaths $$x_t$$	$$ \hat m $$	$$ \hat s $$
2017 Jan	3034	NA	______
2017 Feb	2748	NA	______
2017 Mar	3164	NA	______
2017 Apr	3238	NA	______
2017 May	3416	NA	______
2017 Jun	3492	NA	______
2017 Jul	3730	3351.6	______
2017 Aug	3409	3350	______
2017 Sep	3572	3343.2	______
2017 Oct	3629	3326.2	______
2017 Nov	3408	3316.5	______
2017 Dec	3391	3318.6	______
2018 Jan	3010	3312.1	______
2018 Feb	2734	3308	______
2018 Mar	3015	3311.7	-296.7
2018 Apr	2979	3313.2	-334.2
2018 May	3443	3307.8	135.2
2018 Jun	3514	3292.4	221.6
2018 Jul	3552	3281.1	270.9
2018 Aug	3490	3270.2	219.8
2018 Sep	3579	3259.5	319.5
2018 Oct	3657	3261.2	395.8
2018 Nov	3250	3264.2	-14.2
2018 Dec	3181	3260.5	-79.5
2019 Jan	2948	3256.7	-308.7
2019 Feb	2535	3262.1	-727.1
2019 Mar	2956	3267.1	-311.1
2019 Apr	3079	3259.3	-180.3
2019 May	3417	3254	163
2019 Jun	3449	3257	192
2019 Jul	3527	3256.7	270.3
2019 Aug	3645	3269	376
2019 Sep	3543	3279.1	263.9
2019 Oct	3506	3252.8	253.2
2019 Nov	3274	3228	46
2019 Dec	3228	3248.2	-20.2
2020 Jan	2895	3294.3	-399.3
2020 Feb	2883	3340.3	-457.3
2020 Mar	2850	3384.7	-534.7
2020 Apr	2555	3433.5	-878.5
2020 May	3346	3481.3	-135.3
2020 Jun	4004	3514.8	489.2
2020 Jul	4078	3549.9	528.1
2020 Aug	4199	3567.7	631.3
2020 Sep	4053	3590.7	462.3
2020 Oct	4169	3672.1	496.9
2020 Nov	3757	3758.2	-1.2
2020 Dec	3550	3793.8	-243.8
2021 Jan	3414	3804.8	-390.8
2021 Feb	2792	3816.6	-1024.6
2021 Mar	3492	3831	-339
2021 Apr	3868	3853.3	14.7
2021 May	4098	3875.5	222.5
2021 Jun	4107	3899.8	207.2
2021 Jul	4240	NA	NA
2021 Aug	4320	NA	NA
2021 Sep	4276	NA	NA
2021 Oct	4482	NA	NA
2021 Nov	3977	NA	NA
2021 Dec	3914	NA	NA

Check Your Understanding

• Working with your assigned partner, fill in the missing values of \(\hat s_t\) in the table above.

Seasonally Adjusted Means

Next, we need to compute the mean (across years) of \(\hat s_t\) by month. To compute this, it can be convenient to organize the values of \(\hat s_t\) in a table, where the rows give the year and the columns give the month. We will calculate the mean of the \(\hat s_t\) values for each month. We will call this \(\bar {\hat s_t}\), the unadjusted monthly additive components.

The overall mean of these unadjusted monthly additive components \(\left( \bar {\bar {\hat s_t}} \right)\) will be reasonably close to, but not exactly zero. We adjust these values by subtracting their overall mean, \(\bar{\bar {\hat s_t}}\), from from each of them:

\[ \bar s_t = \bar {\hat s_t} - \bar{\bar {\hat s_t}} \]

where \(\bar {\hat s_t}\) is the mean of the \(\hat s_t\) values corresponding to month \(t\), and \(\bar{\bar {\hat s_t}}\) is the mean of the \(\bar {\hat s_t}\) values.

This yields \(\bar s_t\), the seasonally adjusted mean for each month.

Table 2: Computation of \(\bar s_t\)

Year	Jan	Feb	Mar	Apr	May	Jun	Jul	Aug	Sep	Oct	Nov	Dec
2017	NA	NA	NA	NA	NA	NA	______	______	______	______	______	______
2018	______	______	-296.7	-334.2	135.2	221.6	270.9	219.8	319.5	395.8	-14.2	-79.5
2019	-308.7	-727.1	-311.1	-180.3	163	192	270.3	376	263.9	253.2	46	-20.2
2020	-399.3	-457.3	-534.7	-878.5	-135.3	489.2	528.1	631.3	462.3	496.9	-1.2	-243.8
2021	-390.8	-1024.6	-339	14.7	222.5	207.2	NA	NA	NA	NA	NA	NA
Mean	-350.2	-695.8	-370.4	-344.6	96.3	277.5	361.9	321.5	318.6	362.2	______	______
$$ \bar s_t $$	$$~$$ ______	$$~$$ ______	$$~$$ ______	$$~$$ ______	$$~$$ ______	$$~$$ ______	$$~$$ ______	$$~$$ ______	$$~$$ ______	$$~$$ ______	$$~$$ ______	$$~$$ ______

Check Your Understanding

• The table above gives the values of \(\hat s_t\). Fill in the missing values in the first two rows of the table above. (Note you already computed these.)
• The second-to-last row (labeled “Mean”) gives the values of \(\bar s_t\). Fill in the two missing numbers. We will call these 12 means \(\bar {\hat s_t}\).
• Compute the mean of the \(\bar {\hat s_t}\) values. Call this value \(\bar {\bar {\hat s_t}}\) (This number should be relatively close to 0.)
• Subtract the grand mean \(\bar {\bar {\hat s_t}}\) from the column means \(\bar {\hat s_t}\) to get \(\bar s_t\), the seasonally adjusted mean for month \(t\). (Note that the mean of the \(\bar s_t\) values is 0.)

\[ \bar s_t = \bar {\hat s_t} - \bar {\bar {\hat s_t}} \]

\(\bar s_t\) is the seasonally adjusted mean for month \(t\).

Computing the Random Component and the Seasonally Adjusted Series

We calculate the random component by subtracting the trend and seasonally adjusted mean from the time series:

\[ \text{random component} = x_t - \hat m_t - \bar s_t \]

The seasonally adjusted series is computed by subtracting \(\bar s_t\) from each of the observed values:

\[ \text{seasonally adjusted series} = x_t - \bar s_t \]

Compute the values missing from the table below.

Table 3: Computation of \(\bar s\), the Random Component, and the Seasonally Adjusted Time Series

Month	Deaths $$x_t$$	$$ \hat m $$	$$ \hat s $$	$$ \bar s $$	Random	Seasonally Adjusted $$x_t$$
2017 Jan	3034	NA	NA	______	______	______
2017 Feb	2748	NA	NA	______	______	______
2017 Mar	3164	NA	NA	______	______	______
2017 Apr	3238	NA	NA	______	______	______
2017 May	3416	NA	NA	______	______	______
2017 Jun	3492	NA	NA	______	______	______
2017 Jul	3730	3351.6	378.4	______	______	______
2017 Aug	3409	3350	59	______	______	______
2017 Sep	3572	3343.2	228.8	______	______	______
2017 Oct	3629	3326.2	302.8	______	______	______
2017 Nov	3408	3316.5	91.5	______	______	______
2017 Dec	3391	3318.6	72.4	______	______	______
2018 Jan	3010	3312.1	-302.1	______	______	______
2018 Feb	2734	3308	-574	______	______	______
2018 Mar	3015	3311.7	-296.7	-365.3	68.6	3380.3
2018 Apr	2979	3313.2	-334.2	-339.6	5.4	3318.6
⋮	⋮	⋮	⋮	⋮	⋮	⋮

Class Activity: Computing the Additive Decomposition in R (10 min)

This code calculates the decomposition, including the seasonally adjusted time series, beginning with the tsibble deaths_ts.

Table 4: First Few Rows of the Decomposition of the Traffic Deaths Time Series

# Compute the additive decomposition for deaths_ts
deaths_decompose <- deaths_ts |>
  model(feasts::classical_decomposition(deaths,
          type = "add"))  |>
  components()

First few rows of the deaths_decompose tsibble:

.model	index	deaths	trend	seasonal	random	season_adjust
feasts::classical_decomposition(deaths, type = "add")	2017 Jan	3034	NA	-345.223	NA	3379.223
feasts::classical_decomposition(deaths, type = "add")	2017 Feb	2748	NA	-690.775	NA	3438.775
feasts::classical_decomposition(deaths, type = "add")	2017 Mar	3164	NA	-365.348	NA	3529.348
feasts::classical_decomposition(deaths, type = "add")	2017 Apr	3238	NA	-339.567	NA	3577.567
feasts::classical_decomposition(deaths, type = "add")	2017 May	3416	NA	101.371	NA	3314.629
feasts::classical_decomposition(deaths, type = "add")	2017 Jun	3492	NA	282.496	NA	3209.504
feasts::classical_decomposition(deaths, type = "add")	2017 Jul	3730	3351.583	366.944	11.473	3363.056
feasts::classical_decomposition(deaths, type = "add")	2017 Aug	3409	3350	326.527	-267.527	3082.473
feasts::classical_decomposition(deaths, type = "add")	2017 Sep	3572	3343.208	323.652	-94.86	3248.348
feasts::classical_decomposition(deaths, type = "add")	2017 Oct	3629	3326.208	367.173	-64.381	3261.827
feasts::classical_decomposition(deaths, type = "add")	2017 Nov	3408	3316.542	35.506	55.952	3372.494
feasts::classical_decomposition(deaths, type = "add")	2017 Dec	3391	3318.583	-62.754	135.171	3453.754
feasts::classical_decomposition(deaths, type = "add")	2018 Jan	3010	3312.083	-345.223	43.14	3355.223
feasts::classical_decomposition(deaths, type = "add")	2018 Feb	2734	3308.042	-690.775	116.734	3424.775
⋮	⋮	⋮	⋮	⋮	⋮	⋮

Check Your Understanding

• How do these values from R compare to the ones you computed above?

autoplot(deaths_decompose)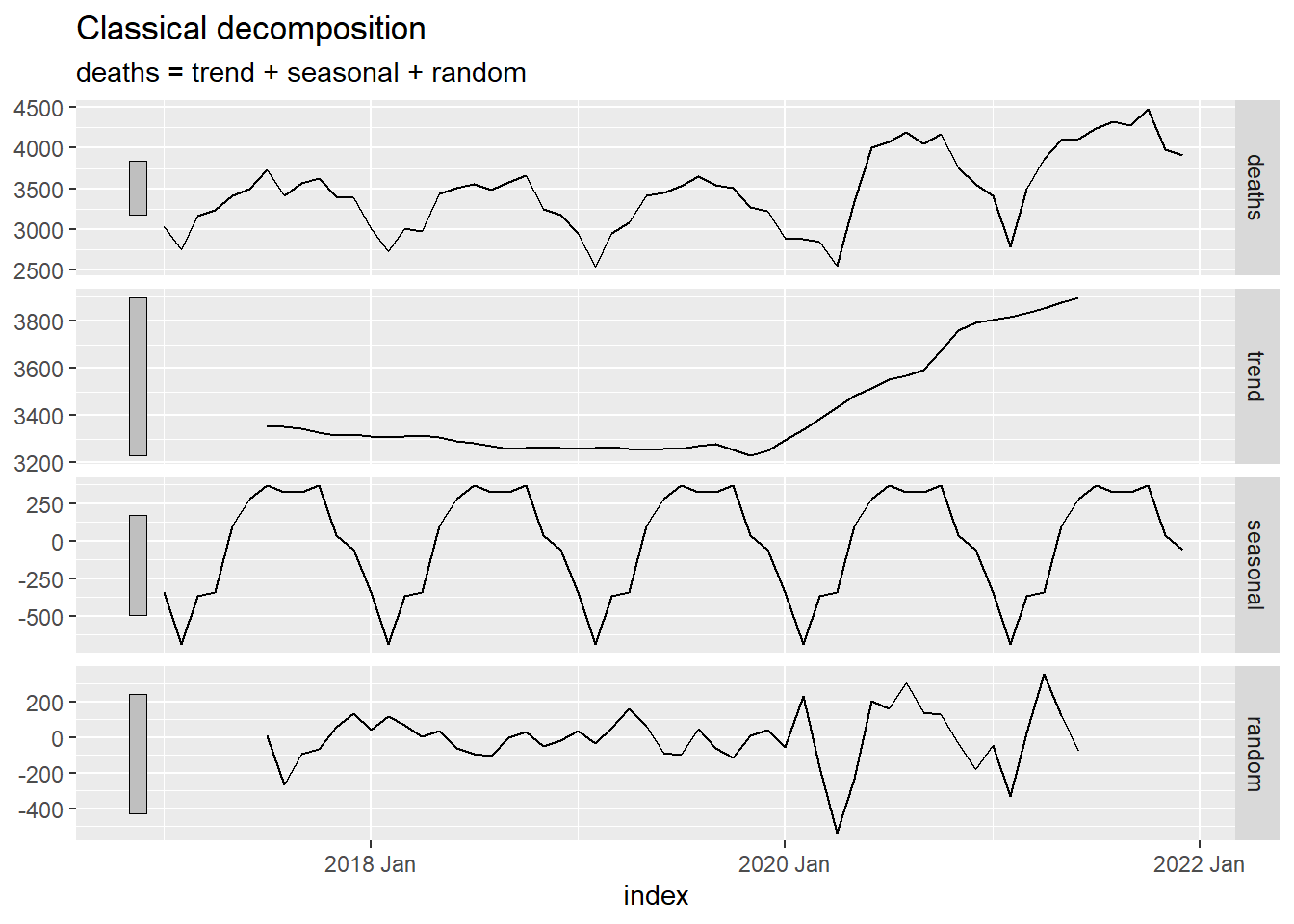

The figure below illustrates the original time series (in black), the centered moving average \(\hat m_t\) (in blue), and the seasonally adjusted series (in red).

deaths_decompose |>
  ggplot() +
  geom_line(data = deaths_decompose, aes(x = index, y = deaths), color = "black") +
  geom_line(data = deaths_decompose, aes(x = index, y = season_adjust), color = "#D55E00") +
  geom_line(data = deaths_decompose, aes(x = index, y = trend), color = "#0072B2") +
  labs(
    x = "Month",
    y = "Traffic Fatalities",
    title = "Traffic Fatalities in the United States (by Month)"
  ) +
  coord_cartesian(ylim = c(0,4500)) +
  theme(plot.title = element_text(hjust = 0.5))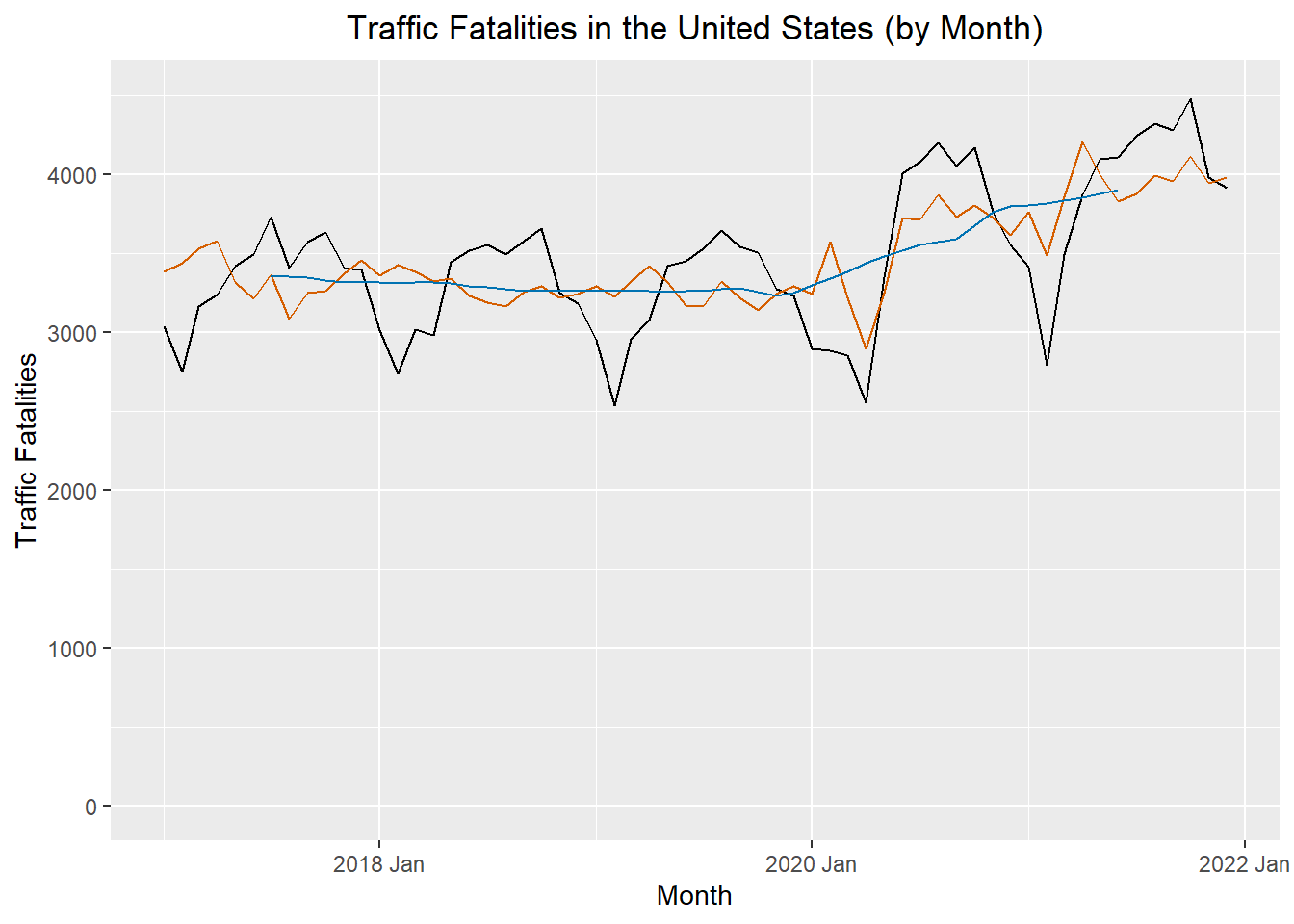

Check Your Understanding

• Do you observe a trend in the time series?
  • What does this trend suggest?
• In February 2020, there is a spike in the seasonally adjusted time series. Refer to the values in the original time series to explain why this occurred.
• In April 2020, there is a dip in the seasonally adjusted time series. Refer to the values in the original time series to explain why this occurred.
  • What would explain this phenomenon?

Homework Preview (5 min)

• Review upcoming homework assignment
• Clarify questions

Homework

Download Assignment

homework_1_4.qmd

Tables-Handout-Excel

Solutions

Tables-Handout-Excel-key

Team Activity: Computational Practice

Solutions for the computations from this lesson

Table 3: (Solutions)

Month	Deaths $$x_t$$	$$ \hat m_t $$	$$ \hat s_t $$	$$ \bar s_t $$	Random	Seasonally Adjusted $$x_t$$
2017 Jan	3034	NA	NA	-345.2	NA	3379.2
2017 Feb	2748	NA	NA	-690.8	NA	3438.8
2017 Mar	3164	NA	NA	-365.3	NA	3529.3
2017 Apr	3238	NA	NA	-339.6	NA	3577.6
2017 May	3416	NA	NA	101.4	NA	3314.6
2017 Jun	3492	NA	NA	282.5	NA	3209.5
2017 Jul	3730	3351.6	378.4	366.9	11.5	3363.1
2017 Aug	3409	3350	59	326.5	-267.5	3082.5
2017 Sep	3572	3343.2	228.8	323.7	-94.9	3248.3
2017 Oct	3629	3326.2	302.8	367.2	-64.4	3261.8
2017 Nov	3408	3316.5	91.5	35.5	56	3372.5
2017 Dec	3391	3318.6	72.4	-62.8	135.2	3453.8
2018 Jan	3010	3312.1	-302.1	-345.2	43.1	3355.2
2018 Feb	2734	3308	-574	-690.8	116.7	3424.8
2018 Mar	3015	3311.7	-296.7	-365.3	68.6	3380.3
2018 Apr	2979	3313.2	-334.2	-339.6	5.4	3318.6
⋮	⋮	⋮	⋮	⋮	⋮	⋮

Table 2: (Solutions)

Year	Jan	Feb	Mar	Apr	May	Jun	Jul	Aug	Sep	Oct	Nov	Dec
2017	NA	NA	NA	NA	NA	NA	378.4	59	228.8	302.8	91.5	72.4
2018	-302.1	-574	-296.7	-334.2	135.2	221.6	270.9	219.8	319.5	395.8	-14.2	-79.5
2019	-308.7	-727.1	-311.1	-180.3	163	192	270.3	376	263.9	253.2	46	-20.2
2020	-399.3	-457.3	-534.7	-878.5	-135.3	489.2	528.1	631.3	462.3	496.9	-1.2	-243.8
2021	-390.8	-1024.6	-339	14.7	222.5	207.2	NA	NA	NA	NA	NA	NA
Mean	-350.2	-695.8	-370.4	-344.6	96.3	277.5	361.9	321.5	318.6	362.2	30.5	-67.8
$$ \bar s_t $$	-345.2	-690.8	-365.4	-339.6	101.3	282.5	366.9	326.5	323.6	367.2	35.5	-62.8