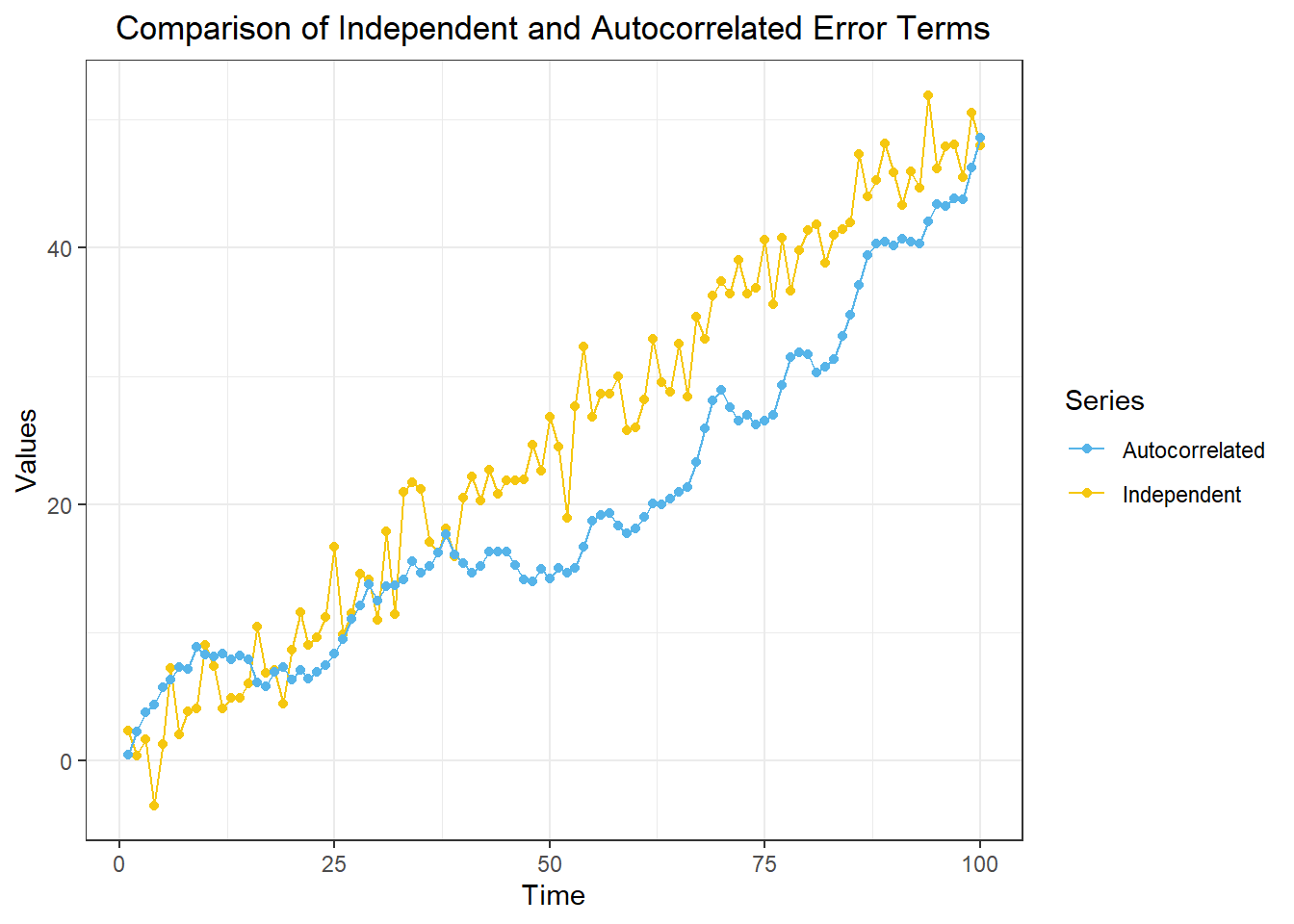
Autocorrelation Concepts

Chapter 2: Lesson 2

Learning Outcomes

Define key terms in time series analysis
  • Define the ensemble of a time series
  • Define the expected value (or mean function) of a time series model
  • Define the sample estimate of the population mean of a time series
  • Define the variance function of a time series model
  • State the constant variance estimator for a time series model
  • Explain the stationarity assumption
  • Explain the stationary variance assumption
  • Define lag
  • Define autocorrelation
  • Define the second-order stationary time series
  • Explain the autocovariance function in Equation (2.11)
  • Explain the lag k autocorrelation function in Equation (2.12)
  • Define the autocovariance function, acvf
  • Define the sample autocorrelation function, acf
Calculate sample estimates of autocovariance and autocorrelation functions from time series data
  • Define the sample autocovariance function, c_k
  • Define the sample autocorrelation function, r_k

Preparation

  • Read Sections 2.2.5

Learning Journal Exchange (10 min)

  • Review another student’s journal
  • What would you add to your learning journal after reading your partner’s?
  • What would you recommend your partner add to their learning journal?
  • Sign the Learning Journal review sheet for your peer

Hands-on Exercise – Exploring Sample Autocorrelation (40 min)

Comparison of Independent and Autocorrelated Error Terms

In the previous lesson, we computed the sample covariance and sample correlation coefficient between two independent variables. When working with time series, the observations are not independent. There is often a relationship between sequential observations. We will compute the autocovariance function and autocorrelation function for a time series. Note: the prefix “auto” comes from a Greek root meaning “self.”

The figure below illustrates the difference between a series of data, where the residuals are independent compared to a series with autocorrelated data.

Check Your Understanding
  • The variances of the residuals for these two series are approximately equal. What characteristics distinguish the two series in the figure above?

Autocovariance and Autocorrelation

We will use the following data to explore the concepts of autovariance and autocorrelation.

t $$ x_t $$
1 4.4
2 4.2
3 4.2
4 4.0
5 4.4
6 4.7
7 4.9
8 5.3
9 5.4
10 5.5

You can use this R command to read in the observations.

x <- c( 4.4, 4.2, 4.2, 4, 4.4, 4.7, 4.9, 5.3, 5.4, 5.5 )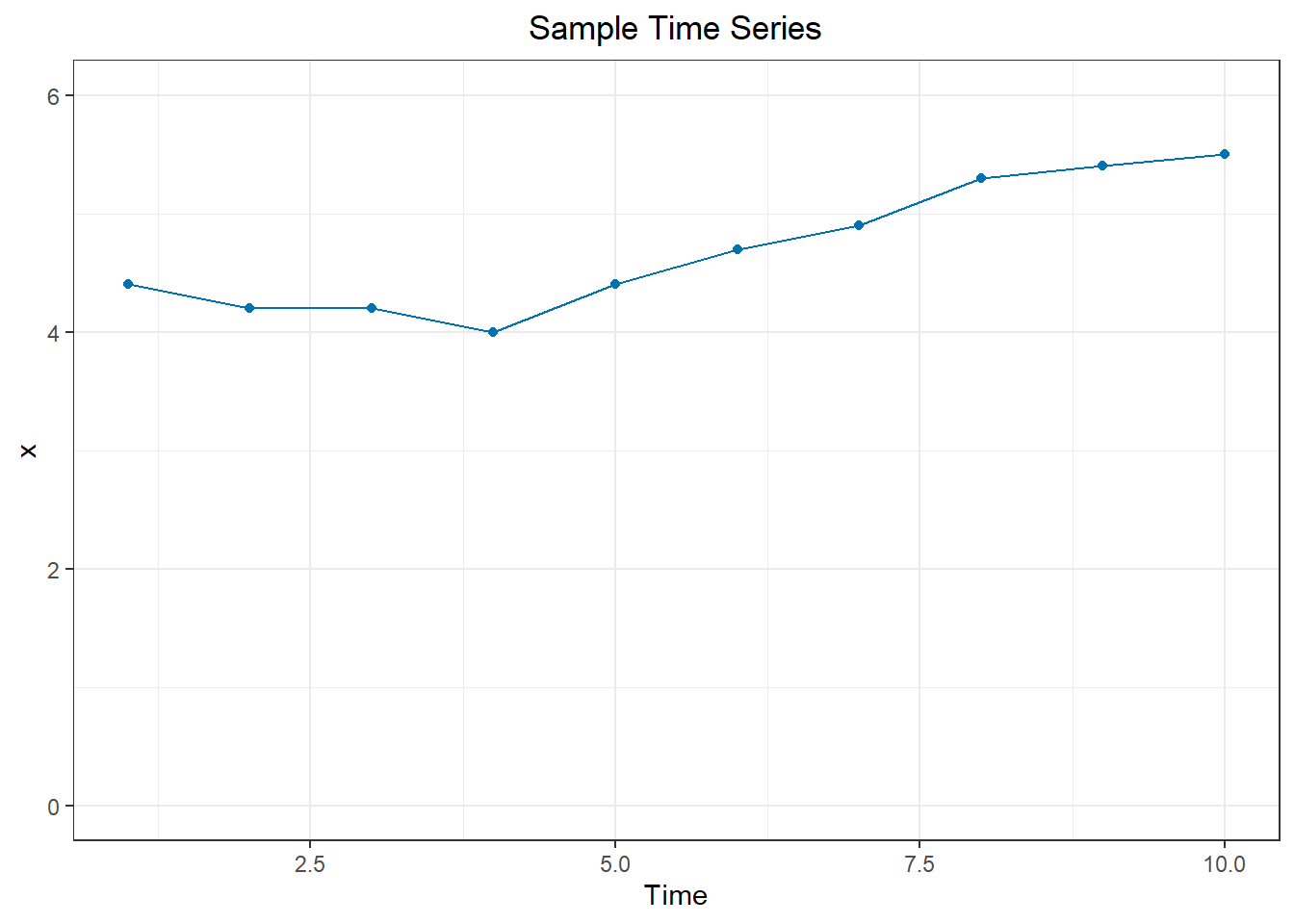

We will use the sample mean of these data repeatedly. The value of \(\bar x\) is:

\[ \bar x = \frac{1}{n} \sum\limits_{t=1}^{n} x_t = \frac{1}{10} \cdot 47 = 4.7 \]

We will be finding the autocovariance and correlation of a time series with itself. First, we start with a lag of 1. With a lag of 1 the corresponding values of the time series that are being compared are shifted by one time unit. Then, we will consider any integer lag: lag \(k\).

Lag \(k\) Sample Autocovariance Function (acvf), \(c_k\)

The lag \(k\) sample autocovariance function, acvf, denoted \(c_k\), is defined as

\[ c_k = \frac{1}{n} \sum\limits_{t=1}^{n-k}(x_t-\bar x)(x_{t+k}-\bar x) \]

We denote the lag by the letter \(k\), where \(k \ge 0\). This is the number of values the data set is shifted to compute the autocovariance.

Check Your Understanding
  • Explain the equation for \(c_k\) to your partner.
  • What is the equation for \(c_0\), the value of the autocovariance function with lag \(k=0\)?
    • This expression is very similar to a definition we have encountered previously. What is it?

Lag \(k=1\) Sample Autocovariance Function, \(c_1\)

We will now find the autocovariance between the values in a time series (\(x = x_t\)) and the same values, shifted by one unit of time (\(y = x_{t+1}\)).

t $$ x_t $$ $$ x_{t+1} $$ $$ x_t-\bar x $$ $$ (x_t-\bar x)^2 $$ $$ x_{t+1}-\bar x$$ $$ (x-\bar x)(x_{t+1}-\bar x) $$
1 4.4 4.2 -0.3 0.09 -0.5 0.15
2 4.2 4.2 -0.5 0.25 -0.5 0.25
3 4.2 4 -0.5 0.25 -0.7 0.35
4 4 4.4 -0.7 0.49 -0.3 0.21
5 4.4 4.7 -0.3 0.09 0 0
6 4.7 4.9 0 0 0.2 0
7 4.9 5.3 0.2 0.04 0.6 0.12
8 5.3 5.4 0.6 0.36 0.7 0.42
9 5.4 5.5 0.7 0.49 0.8 0.56
10 5.5 — 0.8 0.64 — —
sum 47 42.6 0 2.7 0.3 2.06
Check Your Understanding
  • Working with your assigned partner, compute each of the values in row 1 by hand. Recall that \(\bar x = 4.7\).
  • With your partner, add up the values in the last column to verify that the sum is 2.06.

The scatterplot below illustrates the relationship between the observed data (\(x_t\)) and the next observation (\(x_{t+1}\)).

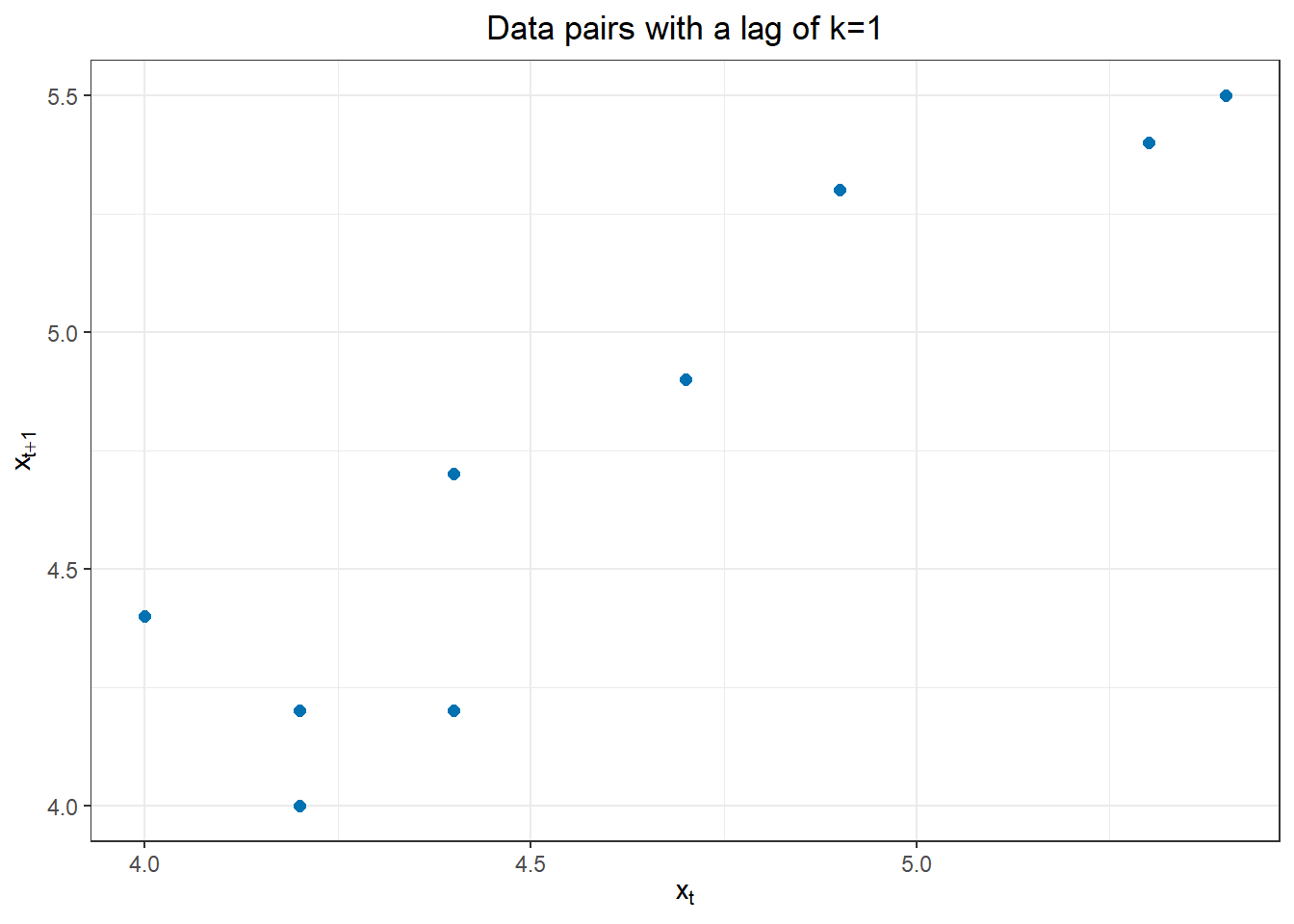
In this example, the second variable is \(x_{t+1}\), where \(t>1\). the autocovariance of \(x_t\) and \(x_{t+1}\) is:

\[ c_1 = \frac{1}{n} \sum\limits_{t=1}^{n-1}(x_t-\bar x)(x_{t+1}-\bar x) = \frac{1}{10} \sum\limits_{t=1}^{9}(x_t-\bar x)(x_{t+1}-\bar x) = \frac{1}{10} \cdot 2.06 = 0.206 \]

This is the (auto)covariance of \(x\) with itself, but with a lag of 1 time unit. This is the value of the lag \(k=1\) autocovariance function, acvf_1.

Check Your Understanding
  • What does the lag 1 autocovariance measure?

Lag \(k\) Sample Autocorrelation Function (acf), \(r_k\)

The sample autocorrelation function, acf, denoted \(r_k\), where \(k\) is the lag, is defined as

\[ r_k = \frac{c_k}{c_0} = \frac{ \frac{1}{n} \sum\limits_{t=1}^{n-k}(x_t-\bar x)(x_{t+k}-\bar x) }{ \frac{1}{n} \sum\limits_{t=1}^{n}(x_t-\bar x)^2 } = \frac{ \sum\limits_{t=1}^{n-k}(x_t-\bar x)(x_{t+k}-\bar x) }{ \sum\limits_{t=1}^{n}(x_t-\bar x)^2 } \]

Note that \(c_0\) is the variance of \(x\), but computed by dividing by \(n\), instead of \(n-1\).

Check Your Understanding
  • Interpret the components of the numerator and the denominator of the expression for \(r_k\) to your partner.

Lag \(k=1\) Sample Autocorrelation Function, \(r_1\)

We can compute the lag 1 autocorrelation or the autocorrelation of \(x\) with lag 1 as the quotient \(r_1 = \frac{c_1}{c_0}\). We have already determined that \(c_1 = 0.206\). We now compute \(c_0\):

\[ c_0 = \frac{1}{n} \sum\limits_{t=1}^{n-0} (x_t-\bar x)(x_{t+0}-\bar x) = \frac{1}{n} \sum\limits_{t=1}^{n} (x_t-\bar x)^2 = \frac{1}{10} \cdot 2.7 = 0.27 \]

We use \(c_0\) and \(c_1\) to compute \(r_1\). Here are two ways we can compute this value:

\[\begin{align*} r_1 &= \frac{c_1}{c_0} = \frac{ \frac{1}{n} \sum\limits_{t=1}^{9}(x_t-\bar x)(x_{t+1}-\bar x) }{ \frac{1}{n} \sum\limits_{t=1}^{10}(x_t-\bar x)^2 } = \frac{ \frac{1}{10} \cdot 2.06 }{ \frac{1}{10} \cdot 2.7 } = \frac{0.206}{0.27} = 0.763 \\ &= \frac{ \sum\limits_{t=1}^{9}(x_t-\bar x)(x_{t+1}-\bar x) }{ \sum\limits_{t=1}^{10}(x_t-\bar x)^2 } = \frac{2.06}{2.7} = 0.763 \end{align*}\]

  • What does the lag 1 autocorrelation, \(c_1\), measure?

Lag \(k = 2\)

Check Your Understanding
  • Working with your assigned partner, fill in the blanks in the following table. Use the results to compute \(c_2\) and \(r_2\).

Tables-Handout-Excel

t $$ x_t $$ $$ x_{t+k} $$ $$ x_t-\bar x $$ $$ (x_t-\bar x)^2 $$ $$ x_{t+k}-\bar x$$ $$ (x-\bar x)(x_{t+k}-\bar x) $$
1 4.4 4.2 -0.3 0.09 -0.5 0.15
2 4.2 4 -0.5 0.25 -0.7 0.35
3 4.2 4.4 -0.5 0.25 -0.3 0.15
4 4
5 4.4
6 4.7
7 4.9 5.4 0.2 0.04 0.7 0.14
8 5.3 5.5 0.6 0.36 0.8 0.48
9 5.4 — 0.7 0.49 — —
10 5.5 — 0.8 0.64 — —
sum 47

The figure below illustrates the relationship between \(x_t\) and \(x_{t+2}\).

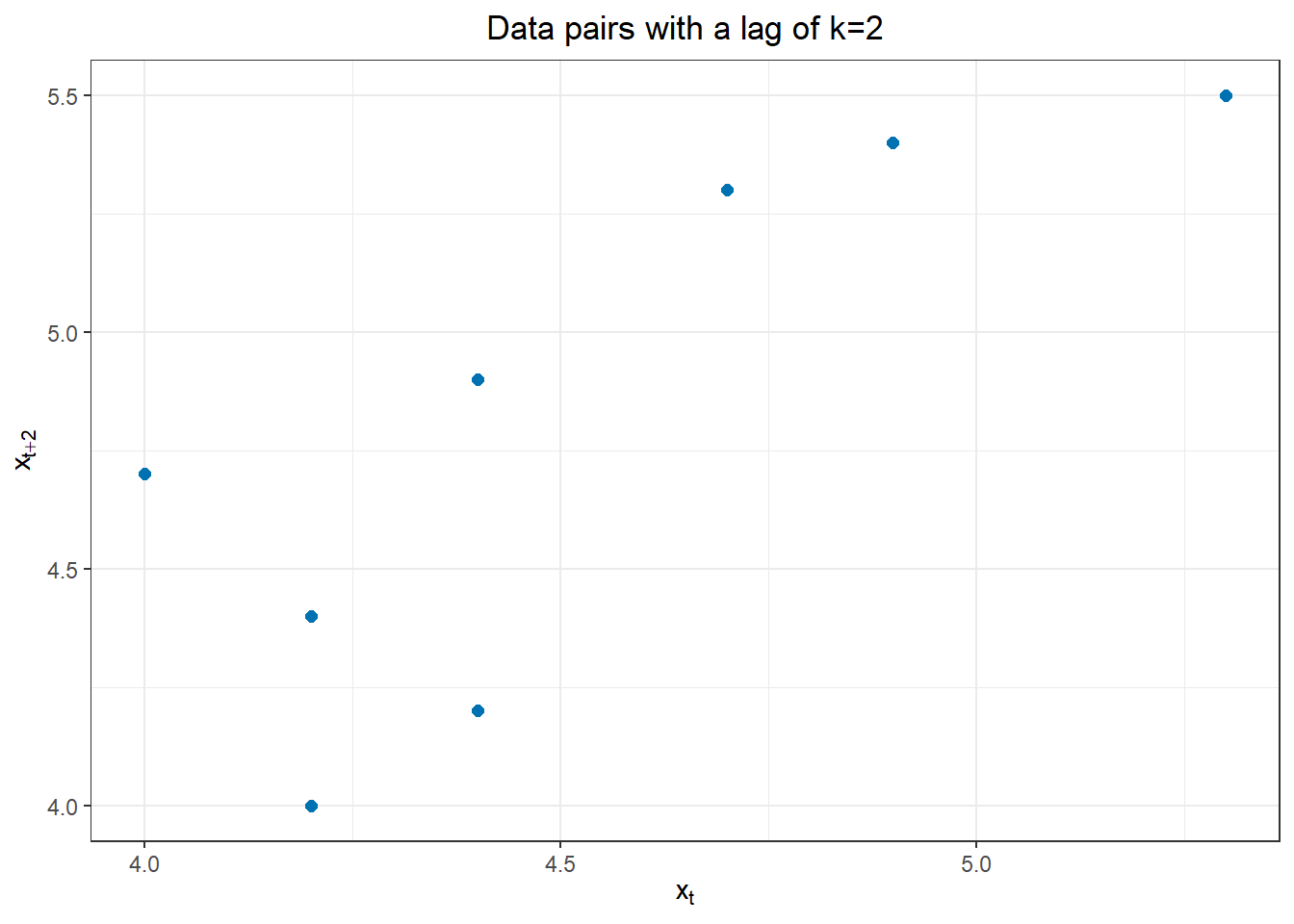
Lag \(k = 3\)

t $$ x_t $$ $$ x_{t+k} $$ $$ x_t-\bar x $$ $$ (x_t-\bar x)^2 $$ $$ x_{t+k}-\bar x$$ $$ (x-\bar x)(x_{t+k}-\bar x) $$
1 4.4 4 -0.3 0.09 -0.7 0.21
2 4.2 4.4 -0.5 0.25 -0.3 0.15
3 4.2 4.7 -0.5 0.25 0 0
4 4 4.9 -0.7 0.49 0.2 -0.14
5 4.4 5.3 -0.3 0.09 0.6 -0.18
6 4.7 5.4 0 0 0.7 0
7 4.9 5.5 0.2 0.04 0.8 0.16
8 5.3 — 0.6 0.36 — —
9 5.4 — 0.7 0.49 — —
10 5.5 — 0.8 0.64 — —
sum 47 34.2 0 2.7 1.3 0.2

The figure below illustrates the correlations between \(x_t\) and \(x_{t+3}\). Note that \(c_3 = \dfrac{0.2}{10} = 0.02\) and \(r_3 = \dfrac{0.02}{0.27} = 0.0741\).

Check Your Understanding
  • Does the value of \(r_3 = 0.0741\) seem reasonable, given the pattern in this plot?

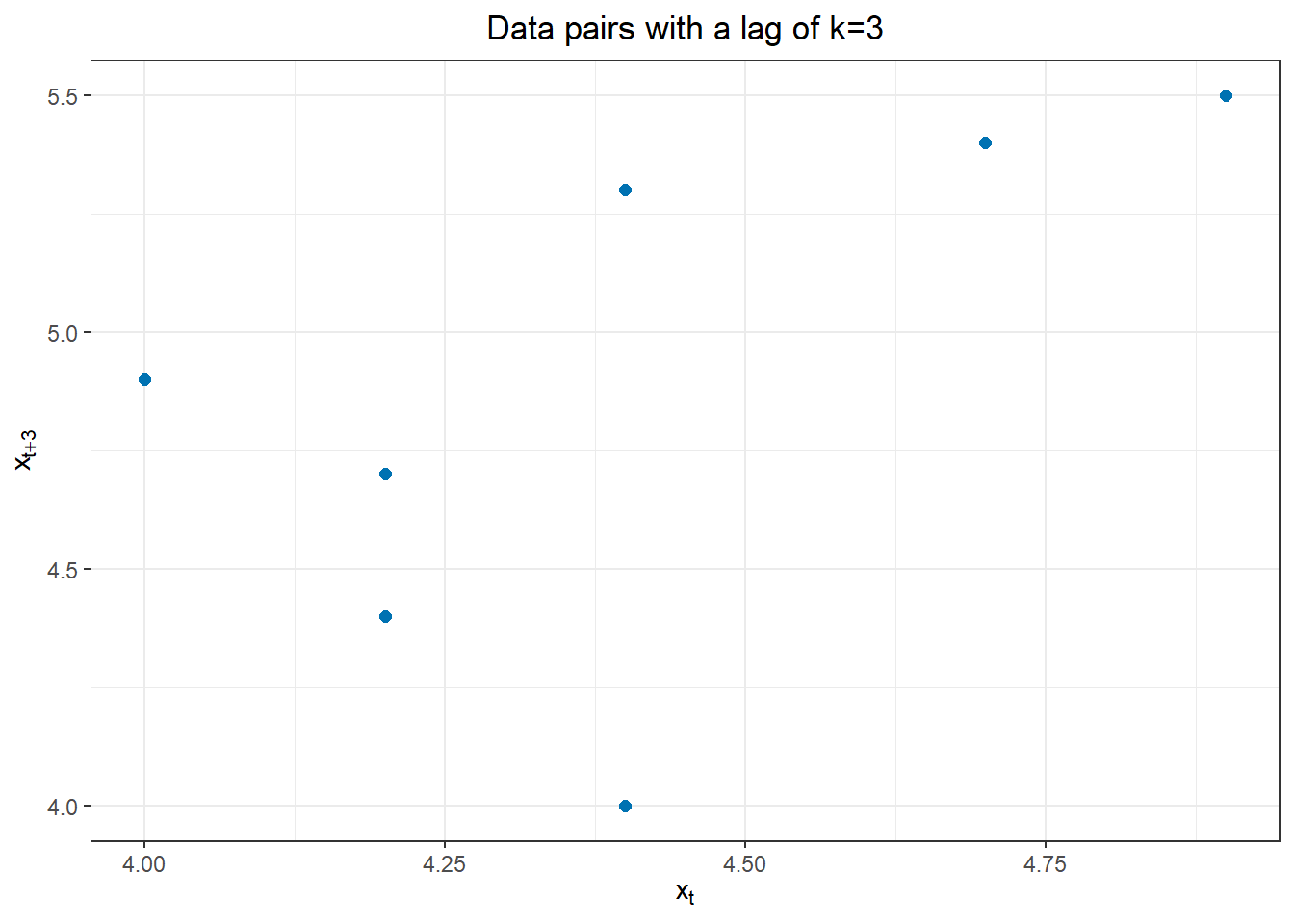
Lag \(k = 4\)

Check Your Understanding
  • Compute \(c_4\) and \(r_4\) using R (but not automated functions), Excel, or hand calculations.
t $$ x_t $$ $$ x_{t+k} $$ $$ x_t-\bar x $$ $$ (x_t-\bar x)^2 $$ $$ x_{t+k}-\bar x$$ $$ (x-\bar x)(x_{t+k}-\bar x) $$
1 4.4
2 4.2
3 4.2
4 4
5 4.4
6 4.7
7 4.9
8 5.3
9 5.4
10 5.5
sum 47

The figure below illustrates the correlations between \(x_t\) and \(x_{t+4}\).

Check Your Understanding
  • Does the value of \(r_4\) you computed seem reasonable, given the pattern in this plot?

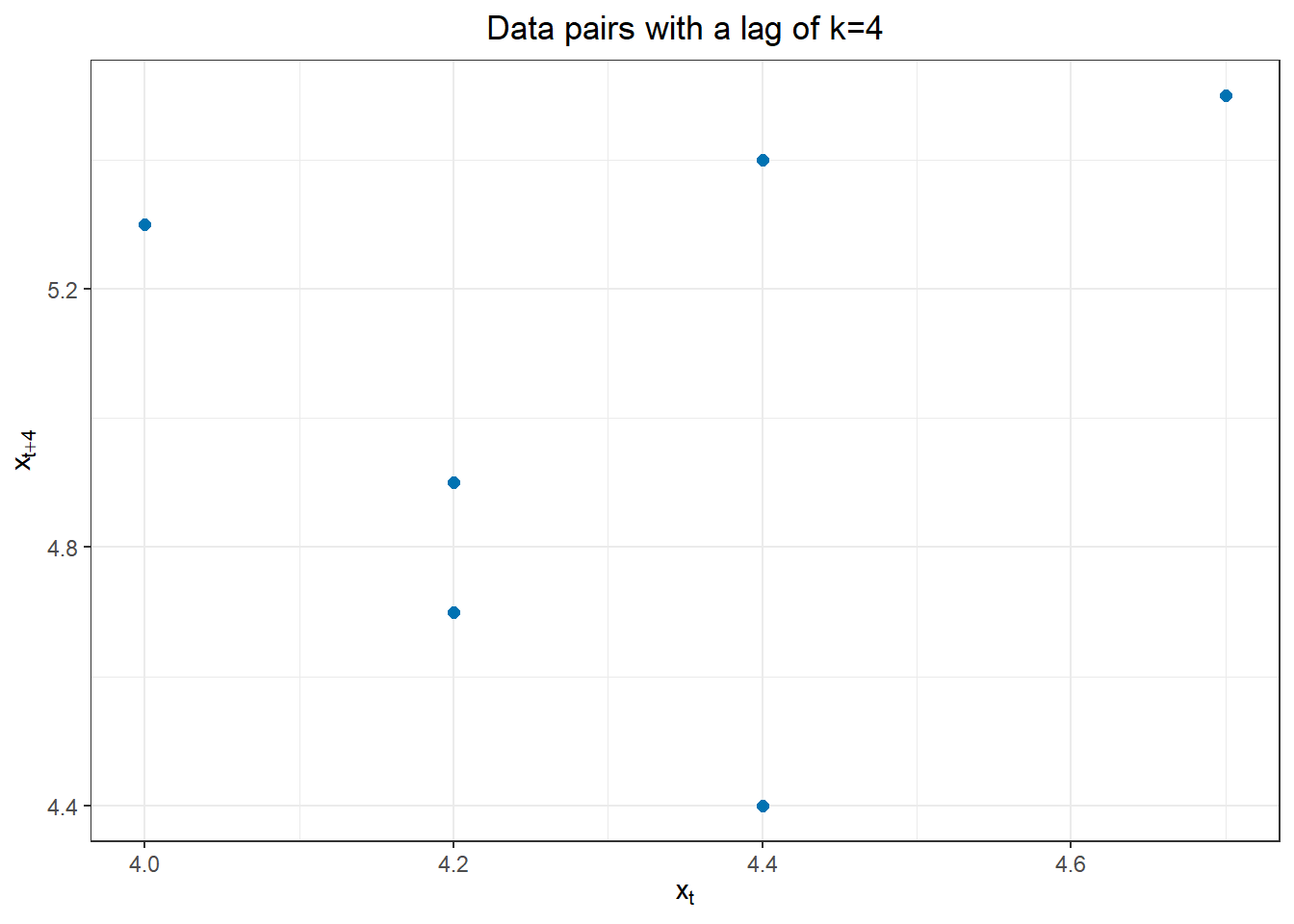
Class Activity: Using R to compute the acvf and acf (5 min)

We will continue to use the following sample data.

 x <- c( 4.4, 4.2, 4.2, 4, 4.4, 4.7, 4.9, 5.3, 5.4, 5.5 ) 
 df <- data.frame(x = x)

acvf

This code gives the values of the acvf.

acf(df$x, plot=FALSE, type = "covariance")

Autocovariances of series 'df$x', by lag

     0      1      2      3      4      5      6      7      8      9 
 0.270  0.206  0.121  0.020 -0.064 -0.113 -0.127 -0.093 -0.061 -0.024

acf

We can obtain the acf by changing the argument for the paramter type to "correlation".

acf(df$x, plot=FALSE, type = "correlation")

Autocorrelations of series 'df$x', by lag

     0      1      2      3      4      5      6      7      8      9 
 1.000  0.763  0.448  0.074 -0.237 -0.419 -0.470 -0.344 -0.226 -0.089

Homework Preview (5 min)

  • Review upcoming homework assignment
  • Clarify questions

Homework

Download Homework

homework_2_2.qmd

Class Activity: k=2

Class Activity: k=4