Seasonal ARIMA Models

Chapter 7: Lesson 2

Learning Outcomes

Identify seasonal ARIMA models
  • Define seasonal ARIMA models and their notation (p, d, q)(P, D, Q)[m]
  • Identify the need for seasonal ARIMA models in time series with seasonal patterns
Apply the fitting procedure for seasonal ARIMA models
  • Describe the steps involved in fitting seasonal ARIMA models
  • Determine the appropriate order of differencing (d and D) based on ACF/PACF plots
  • Select the order of AR and MA terms (p, q, P, Q) using ACF/PACF plots and model selection criteria
Fit seasonal ARIMA models to time series data using R
  • Use R to fit seasonal ARIMA models
  • Interpret the output for the ARIMA models, including coefficients and model diagnostics
  • Forecast future values using the fitted seasonal ARIMA model

Preparation

  • Read Section 7.3

Learning Journal Exchange (10 min)

  • Review another student’s journal

  • What would you add to your learning journal after reading another student’s?

  • What would you recommend the other student add to their learning journal?

  • Sign the Learning Journal review sheet for your peer

Definition of Seasonal ARIMA (SARIMA) Models

We can add a seasonal component to an ARIMA model. We call this model a Seasonal ARIMA model, or a SARIMA model. We use differencing at a lag equal to the number of seasons, \(s\). This allows us to remove additional seasonal effects that carry over from one cycle to another.

Recall that if we use a difference of lag 1 to remove a linear trend, we introduce a moving average term. The same thing happens when we introduce a difference with lag \(s\). For the lag \(s\) values, we can apply an autoregressive (AR) component at lag \(s\) with \(P\) parameters, an integrated (I) component with parameter \(D\), and a moving average (MA) component with \(Q\) terms. This yields the full SARIMA model.

Definition of SARIMA Models

A Seasonal ARIMA model, or SARIMA model with \(s\) seasons can be expressed as:

\[ \Theta_P \left( \mathbf{B}^s \right) \theta_p \left( \mathbf{B} \right) \left( 1 - \mathbf{B}^s \right)^D \left( 1 - \mathbf{B} \right)^d x_t = \Phi_Q \left( \mathbf{B}^s \right) \phi_q \left( \mathbf{B} \right) w_t \]

where

  • \(p\), \(d\), and \(q\) are the parameters for the \(ARIMA(p, d, q)\) model applied to the time series and the differences are taken with a lag of 1,

  • \(s\) is the number of seasons, and

  • \(P\), \(D\), and \(Q\) are the parameters for the \(ARIMA(P, D, Q)\) model applied to the time series where the differences are taken across a lag of \(s\).

\(\Theta_P \left( \mathbf{B}^s \right)\), \(\theta_p \left( \mathbf{B} \right)\), \(\Phi_Q \left( \mathbf{B}^s \right)\), and \(\phi_q \left( \mathbf{B} \right)\) are polynomials of degree \(P\), \(p\), \(Q\), and \(q\), respectively.

We denote this model as \(ARIMA(p,d,q)(P,D,Q)_s\) or \(ARIMA(p,d,q)(P,D,Q)[s]\).

Looking closely at this model, we can see it is the combination of the ARIMA model \[ \theta_p \left( \mathbf{B} \right) \left( 1 - \mathbf{B} \right)^d x_t = \phi_q \left( \mathbf{B} \right) w_t \] and the same model, after applying a difference across \(s\) seasons \[ \Theta_P \left( \mathbf{B}^s \right) \left( 1 - \mathbf{B}^s \right)^D x_t = \Phi_Q \left( \mathbf{B}^s \right) w_t \]

Special Cases of a Seasonal ARIMA Model

Stationary SARIMA Models

Stationarity of SARIMA Models

The SARIMA model is, in general, non-stationary. However, there is a special case in which it is stationary. An \(ARIMA(p,d,q)(P,D,Q)_s\) will be stationary if the following conditions are satisfied:

  1. If \(D = d = 0\), and
  2. The roots of the characteristic equation \[ \Theta_P \left( \mathbf{B}^s \right) \theta_p \left( \mathbf{B} \right) = 0 \] are all greter than 1 in absolute value.

A Simple AR Model with a Seasonal Period of \(s\) Units

\(ARIMA(0,0,0)(1,0,0)_{s}\) is given as

\[ x_t = \alpha x_{t-s} + w_t \] This model would be appropriate for data where there are \(s\) seasons and the value in the season exactly one cycle prior affects the current value. This model is stationary when \(\left| \alpha^{1/s} \right| > 1\).

Simple Quarterly Seasonal Moving Average Model (with no Trend)

We can write a simple quarterly seasonal moving average model as

\[ x_t = \underbrace{w_t - \beta w_{t-4}}_{\left( 1 - \beta \mathbf{B}^{4} \right) w_t} \]

This is an \(ARIMA(0,0,0)(0,0,1)_4\) model.

Quarterly Seasonal Moving Average Model with a Stocastic Trend

We can add a stochastic trend to the previous model by including first-order differences:

\[ x_t = x_{t-1} + w_t - \beta w_{t-4} \] This is an \(ARIMA(0,1,0)(0,0,1)_4\) model.

Quarterly Seasonal Moving Average Model where the Seasonal Terms Contain a Stocastic Trend

We can allow the seasonal components to include a stochastic trend. We apply differencing at the seasonal period. This yields the model

\[ x_t = x_{t-4} + w_t - \beta w_{t-4} \]

This is an \(ARIMA(0,0,0)(0,1,1)_4\) process.

Effects of Differencing

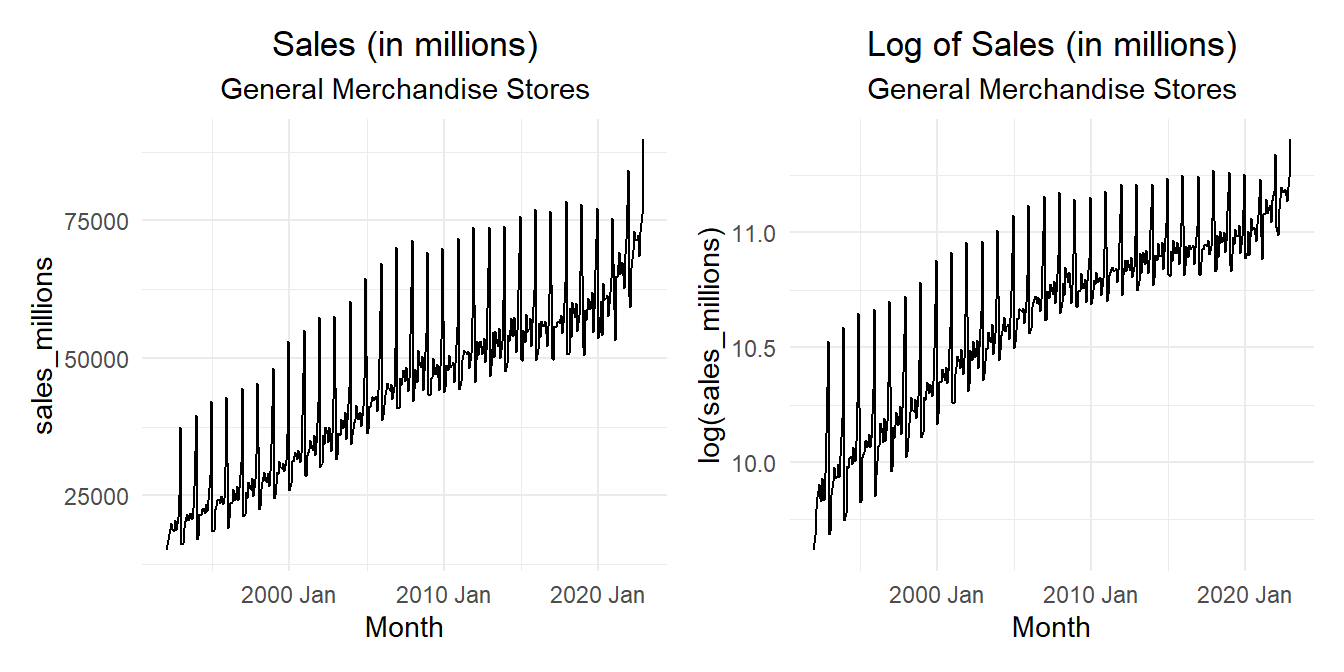
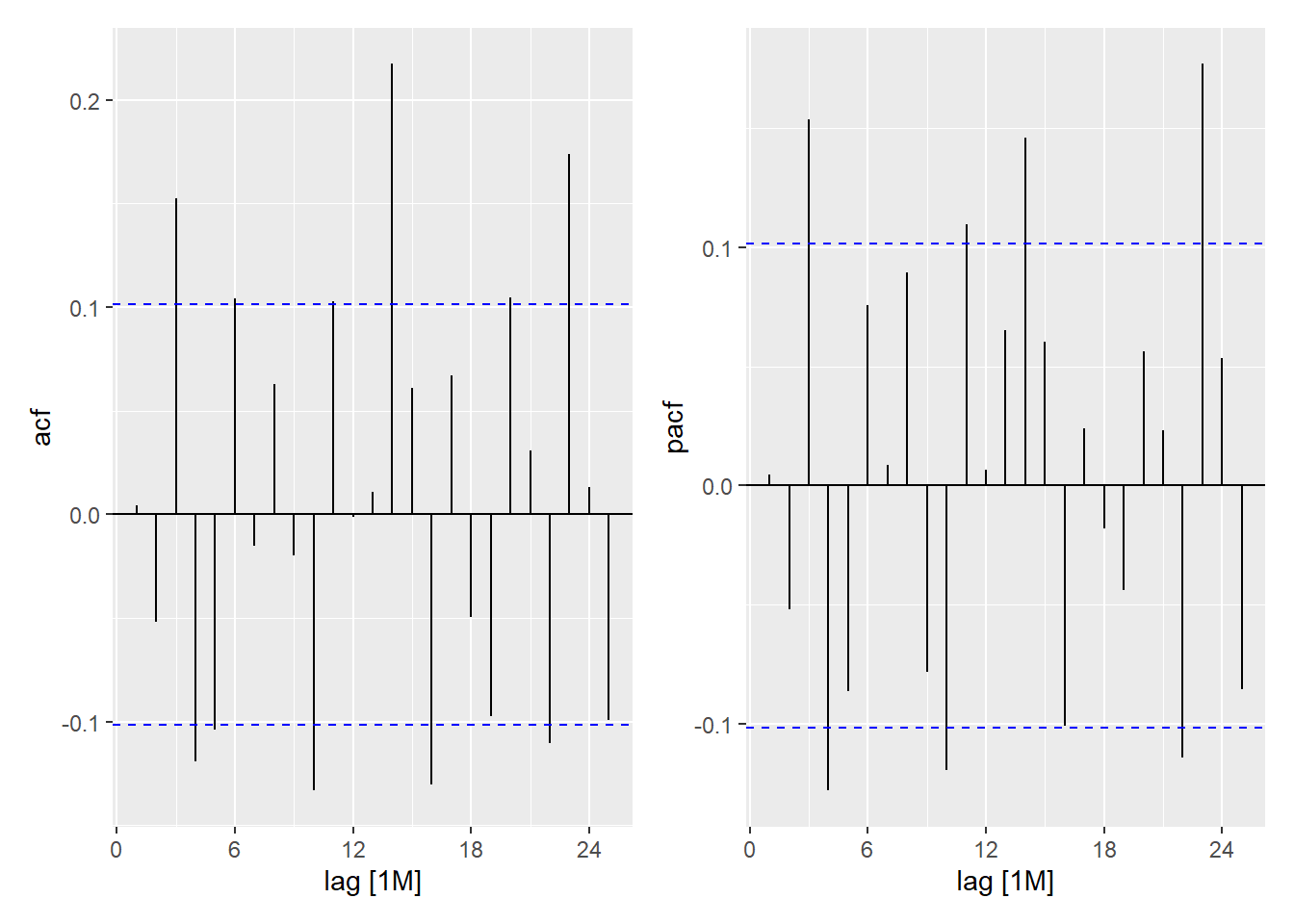
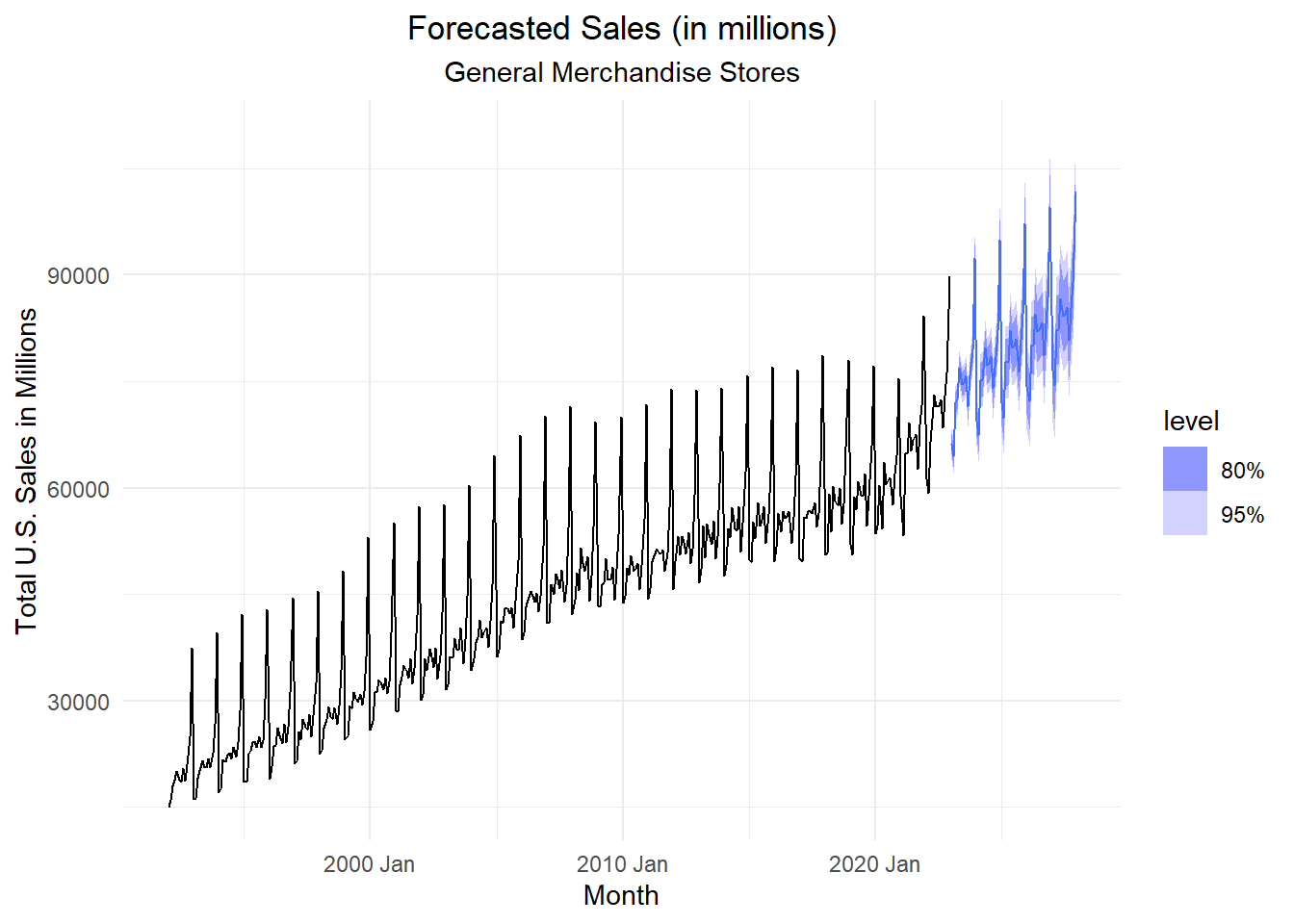
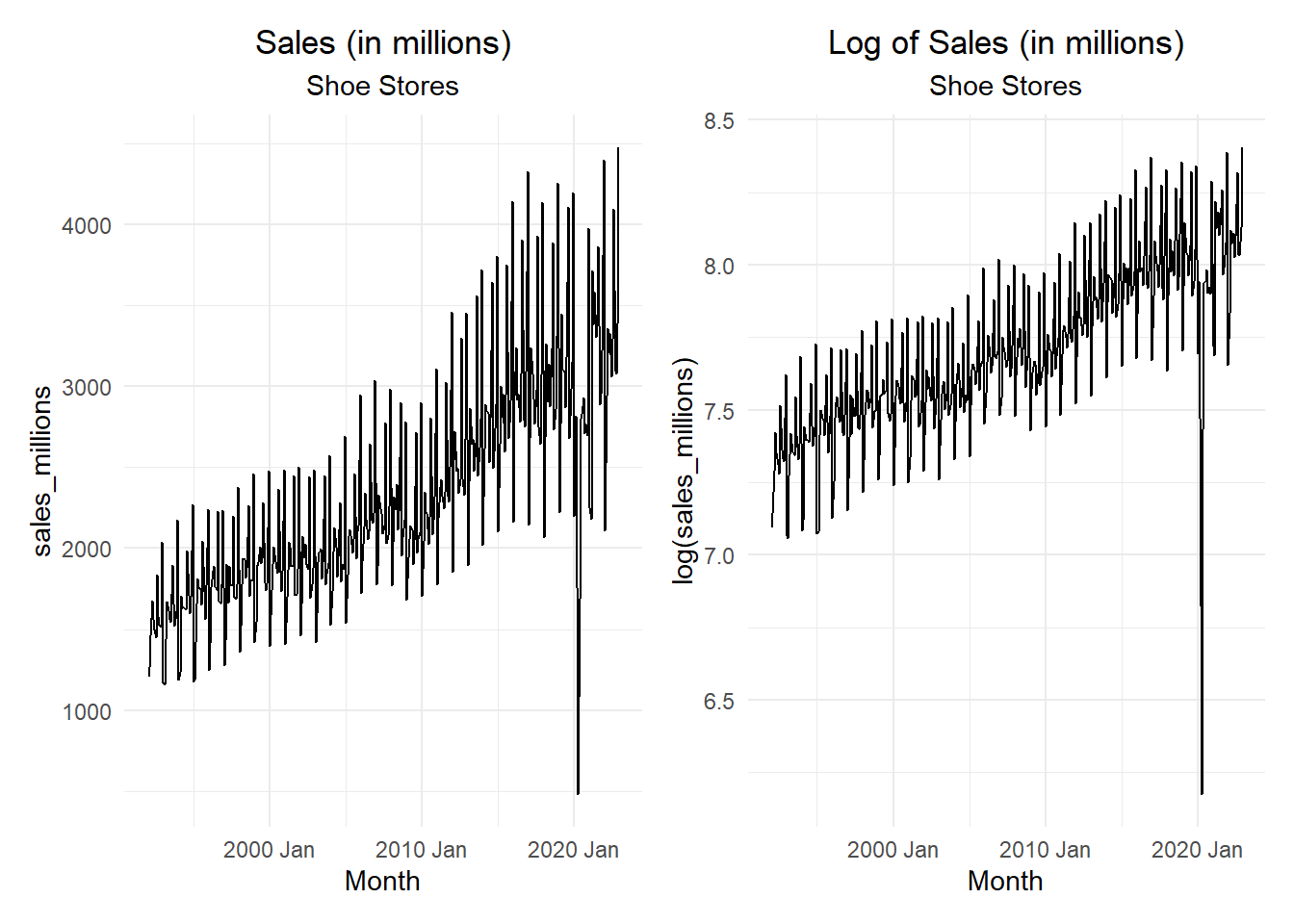
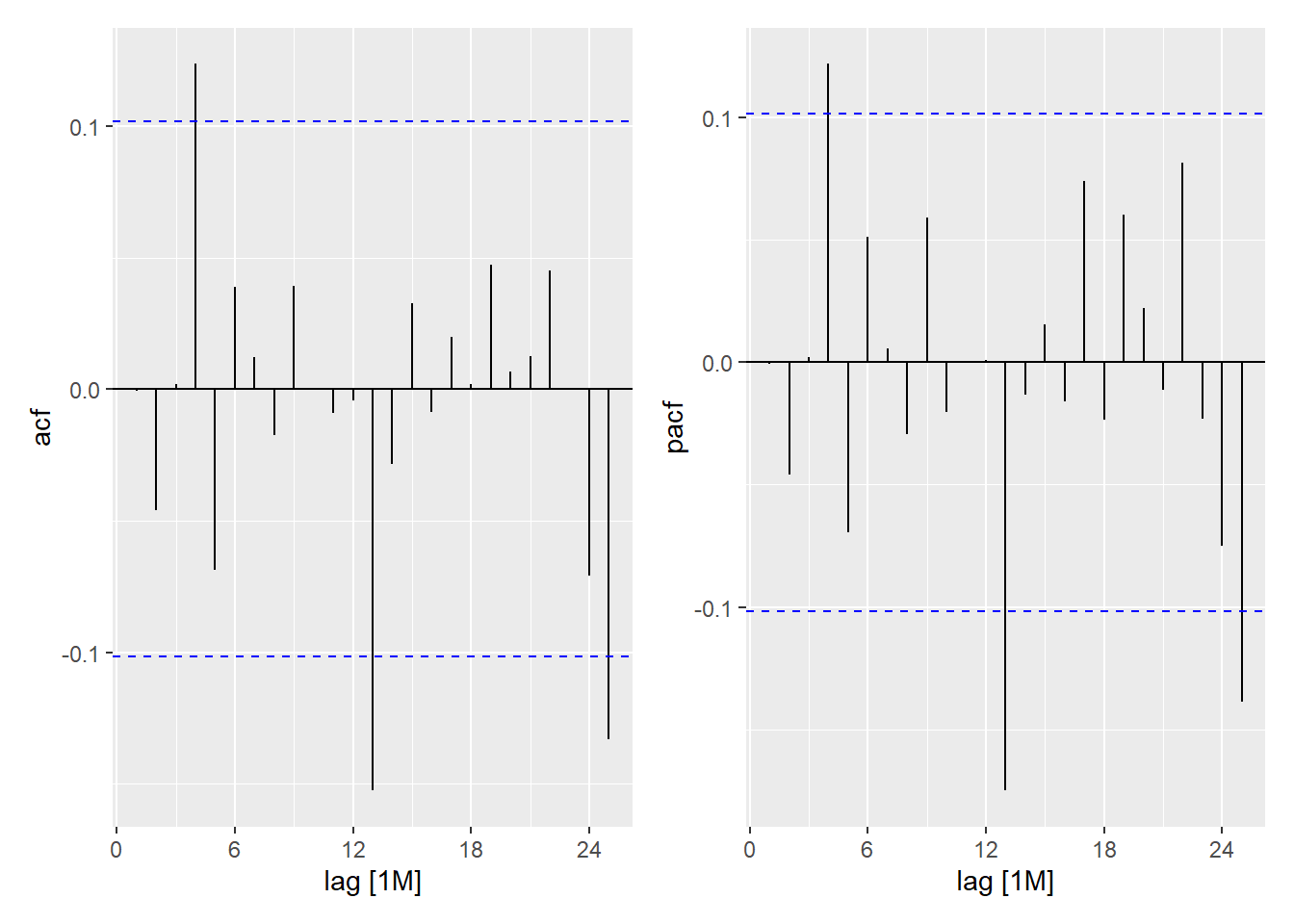
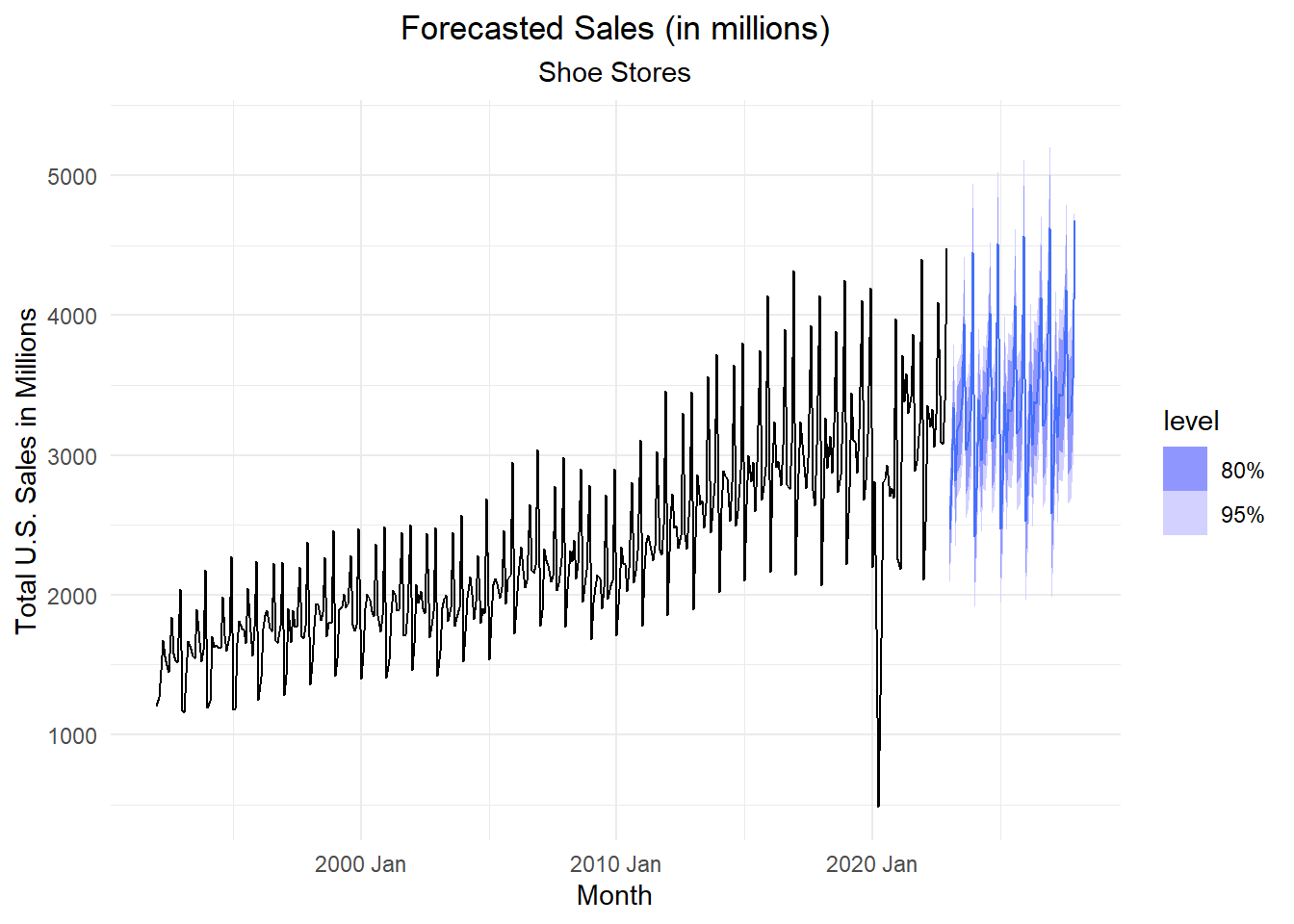
Recall that lag \(s\) differencing will remove a linear trend, however if there is a linear trend, differencing at lag 1 will introduce an AR process in the residuals. If a linear model is appropriate in a, say, quarterly series with additive seasonals, then the model could be \[ x_t = a + bt + s_{[t]} + w_t \]

where \([t]\) is the modulus operator, or \([t]\) is the remainder when \(t\) is divided by \(4\). Another way to view this is to note that for a quarterly time series, \([t] = [t-4]\).

If we apply first-order differencing at lag 4, we get \[\begin{align*} \left( 1 - \mathbf{B}^{4} \right) x_t &= x_t - x_{t-4} \\ &= \left(a + bt + s_{[t]} + w_t \right) - \left(a + b(t-4) + s_{[t-4]} + w_{t-4} \right) \\ &= \left(a + bt + s_{[t]} + w_t \right) - \left(a + b(t-4) + s_{[t]} + w_{t-4} \right) \\ &= 4b + w_t - w_{t-4} \end{align*}\]

This is an \(ARIMA(0,0,0)(0,1,1)_4\) process with constant term of \(4b\).

If we apply first-order differencing at lag 1 and then do the differencing at lag 4, we get the following process: \[\begin{align*} \left( 1 - \mathbf{B}^{4} \right) \left( 1 - \mathbf{B} \right) x_t &= \left( 1 - \mathbf{B}^{4} \right) \left( x_t - \mathbf{B}x_t \right) \\ &= \left( 1 - \mathbf{B}^{4} \right) \left[ \left( a + bt + s_{[t]} + w_t \right) - \mathbf{B} \left( a + bt + s_{[t]} + w_t \right) \right] \\ &= \left( 1 - \mathbf{B}^{4} \right) \left[ \left( a + bt + s_{[t]} + w_t \right) - \left( a + b(t-1) + s_{[t-1]} + w_{t-1} \right) \right] \\ &= \left( 1 - \mathbf{B}^{4} \right) \left[ \left( s_{[t]} + w_t \right) - \left( -b + s_{[t-1]} + w_{t-1} \right) \right] \\ &= \left( 1 - \mathbf{B}^{4} \right) \left( b + s_{[t]} - s_{[t-1]} + w_t - w_{t-1} \right) \\ &= \left( b + s_{[t]} - s_{[t-1]} + w_t - w_{t-1} \right) - \mathbf{B}^{4} \left( b + s_{[t]} - s_{[t-1]} + w_t - w_{t-1} \right) \\ &= \left( b + s_{[t]} - s_{[t-1]} + w_t - w_{t-1} \right) - \left( b + s_{[t-4]} - s_{[t-5]} + w_{t-4} - w_{t-5} \right) \\ &= \left( s_{[t]} - s_{[t-1]} + w_t - w_{t-1} \right) - \left( s_{[t]} - s_{[t-1]} + w_{t-4} - w_{t-5} \right) \\ &= w_t - w_{t-1} - w_{t-4} + w_{t-5} \end{align*}\]

This represents an \(ARIMA(0,1,1)(0,1,1)_4\) process without a constant term.

Class Activity: Seasonal ARIMA Models - Retail: General Merchandise Stores (10 min)

Show the code 
# Read in retail sales data for "Full-Service Restaurants"
retail_ts <- rio::import("https://byuistats.github.io/timeseries/data/retail_by_business_type.parquet") |>
  filter(naics == 452) |>
  mutate( month = yearmonth(as_date(month)) ) |>
  na.omit() |>
  as_tsibble(index = month)

retail_plot_raw <- retail_ts |>
    autoplot(.vars = sales_millions) +
    labs(
      x = "Month",
      y = "sales_millions",
      title = "Sales (in millions)",
      subtitle = "General Merchandise Stores"
    ) +
    theme_minimal() +
    theme(
      plot.title = element_text(hjust = 0.5),
      plot.subtitle = element_text(hjust = 0.5)
    )

retail_plot_log <- retail_ts |>
    autoplot(.vars = log(sales_millions)) +
    labs(
      x = "Month",
      y = "log(sales_millions)",
      title = "Log of Sales (in millions)",
      subtitle = "General Merchandise Stores"
    ) +
    theme_minimal() +
    theme(
      plot.title = element_text(hjust = 0.5),
      plot.subtitle = element_text(hjust = 0.5)
    )

retail_plot_raw | retail_plot_log
Figure 1: Time plots of the retail sales in General Merchandise stores; time plot of the timt series (left) and the natural logarithm of the time series (right)
Check Your Understanding
  • Based on the figure above, should the logarithm be applied to the time series? Justify your answer.

Here are a few models we could fit to this time series.

Show the code 
retail_ts |>
  model(
    ar_model = ARIMA(sales_millions ~ 1 +
      pdq(1, 1, 0) +
      PDQ(1, 0, 0), approximation = TRUE),
    ma_model = ARIMA(sales_millions ~ 1 + 
      pdq(0, 1, 1) +
      PDQ(0, 0, 1), approximation = TRUE),
    arima_102012 = ARIMA(sales_millions ~ 1 + 
      pdq(1, 0, 2) +
      PDQ(0, 1, 2), approximation = TRUE),
    arima_102102 = ARIMA(sales_millions ~ 1 + 
      pdq(1, 0, 2) +
      PDQ(1, 0, 2), approximation = TRUE),
    arima_112112 = ARIMA(sales_millions ~ 1 + 
      pdq(1, 1, 2) +
      PDQ(1, 1, 2), approximation = TRUE),
    arima_012012 = ARIMA(sales_millions ~ 1 + 
      pdq(0, 1, 2) +
      PDQ(0, 1, 2), approximation = TRUE),
    arima_111111 = ARIMA(sales_millions ~ 1 + 
      pdq(1, 1, 1) +
      PDQ(1, 1, 1), approximation = TRUE),
    ) |>
  glance()
.model sigma2 log_lik AIC AICc BIC
ar_model 1887684 -3227.047 6462.094 6462.204 6477.759
ma_model 15542235 -3605.992 7219.985 7220.094 7235.650
arima_102012 1264061 -3038.772 6091.544 6091.862 6118.747
arima_112112 1272651 -3030.991 6077.982 6078.393 6109.048
arima_012012 1266582 -3031.167 6074.333 6074.572 6097.633
arima_111111 1270495 -3031.753 6075.506 6075.745 6098.806

Here is the model automatically selected by R.

Show the code 
best_fit_retail <- retail_ts |>
  model(
    ar_model = ARIMA(sales_millions ~ 1 +
      pdq(0:2, 0:2, 0:2) +
      PDQ(0:2, 0:2, 0:2), approximation = TRUE))

best_fit_retail
# A mable: 1 x 1
                            ar_model
                             <model>
1 <ARIMA(1,0,2)(0,1,2)[12] w/ drift>

This is the acf and pacf of the residuals from the automatically selected model.

Show the code 
acf_plot <- best_fit_retail |>
  residuals() |>
  feasts::ACF() |>
  autoplot()

pacf_plot <- best_fit_retail |>
  residuals() |>
  feasts::PACF() |>
  autoplot()

acf_plot | pacf_plot
Figure 2: Correlogram (left) and partial correlogram (right) of the residuals from the best-fitting model
Check Your Understanding
  • What do you notice in the acf and pacf plots?

Here are the coefficients from the automatically-selected model.

Show the code 
coefficients(best_fit_retail)
.model term estimate std.error statistic p.value
ar_model ar1 0.9783222 0.0159629 61.287161 0.0000000
ar_model ma1 -0.8326530 0.0542793 -15.340162 0.0000000
ar_model ma2 0.1720797 0.0561780 3.063116 0.0023554
ar_model sma1 -0.4200558 0.0535544 -7.843536 0.0000000
ar_model sma2 -0.0980853 0.0515993 -1.900905 0.0581129
ar_model constant 39.3324809 9.4755984 4.150923 0.0000414

We can forecast future values of this time series using our model.

Show the code 
best_fit_retail |>
  forecast(h = "60 months") |>
  autoplot(retail_ts) +
    labs(
      x = "Month",
      y = "Total U.S. Sales in Millions",
      title = "Forecasted Sales (in millions)",
      subtitle = "General Merchandise Stores"
    ) +
    theme_minimal() +
    theme(
      plot.title = element_text(hjust = 0.5),
      plot.subtitle = element_text(hjust = 0.5)
    )
Figure 3: Five-year forecast of the time series based on the best-fitting model
Check Your Understanding
  • How well does the forecast generated by this model appear to work?

Small-Group Activity: Seasonal ARIMA Models - Retail: Shoe Stores (20 min)

Check Your Understanding

Repeat the analysis above for the retail sales for shoe stores (NAICS code 4482).

  • Create time plots of the data and the logarithm of the data.
  • Is it appropriate to take the logarithm of the time series? (Use the appropriate time series for the following.)
  • Find the best-fitting SARIMA model for the time series.
  • Determine the model coefficients.
  • Use the acf and pacf plots of the residuals to assess whether this model adequately models the time series.
  • Use your model to forecast the value of the time series over the next five years.
  • How well does the forecast generated by this model appear to work?
  • Did the downward COVID spike seriously affect the applicability of this model?

Homework Preview (5 min)

  • Review upcoming homework assignment
  • Clarify questions
Download Homework

homework_7_2.qmd

Small-Group Activity: Seasonal ARIMA Models - Retail: Shoe Stores