Multiplicative Models

Chapter 1: Lesson 5

Learning Outcomes

Decompose time series into trends, seasonal variation, and residuals
  • Explain the differences between additive and multiplicative models
  • Implement multiplicative decomposition
  • Compute the estimators of seasonal variation for a multiplicative model
  • Calculate the random component for a multiplicative model
  • Compute a seasonally-adjusted time series based on a multiplicative model

Preparation

  • Review Sections 1.5.1-1.5.3

Learning Journal Exchange (10 min)

  • Review another student’s journal
  • What would you add to your learning journal after reading your partner’s?
  • What would you recommend your partner add to their learning journal?
  • Sign the Learning Journal review sheet for your peer

Class Activity: Comparing Models in the Textbook Versus R (2 min)

Both the textbook and R use the same model in the additive case:

\[ x_t = m_t + s_t + z_t \]

However, there is a discrepancy in the definitions for the mulitplicative models. The textbook defines the multiplicative model as

\[ x_t = m_t \cdot s_t + z_t \] but R defines the multiplicative model as

\[ x_t = m_t \cdot s_t \cdot z_t \] You can investigate R’s definition by executing this command in RStudio.

?classical_decomposition

Class Activity: Exploring Simulated Time Series Data (10 min)

So far, you have learned how to estimate a trend using aggregated data (i.e., an annual average) or a moving average. We will compute the seasonal effect and use this to get the random component.

Additive Model

The code hidden below simulates 10 years of a monthly time series with a linear trend and seasonal variation based on an additive model. Because the data are simulated, we know exactly which functions were used to create it, and we can observe what happens when we decompose this function.

Table 1: Simulated Data (Additive Model)

Show the code 
# Set random seed for reproducibility
set.seed(20) 

# Set parameters & initialize vectors
num_years <- 10
n <- 12 * num_years
sigma <- .75
a <- 0.05
b <- 1
c <- 0.5
trend <- seasonal <- x_t <- rep(0,n)
time_seq <- seq(1,n)

# Generate correlated error terms
w <- rnorm(n + 4, 0, 1)
z = w + lead(w,1) + lead(w,2) + lead(w,3) + lead(w,4)
z  = head(z, n) / 2

# Get date
year_seq <- lubridate::year(today()) - num_years  + (time_seq - 1) %/% 12
month_seq <- (time_seq - 1) %% 12 + 1
date_seq <- ymd(paste0(year_seq,"-",month_seq,"-01"))

# Get data
for (t in 1:n) {
  trend[t] <- a * t + 10
  seasonal[t] <- b * sin(t / 12 * 2 * pi * 1)  + c * cos(t / 12 * 2 * pi * 3)
  x_t[t] <- trend[t] + seasonal[t] + z[t]
}

x_df <- data.frame(x_t = x_t, trend = trend, seasonal = seasonal)

start_year <- lubridate::year(today()) - num_years
start_date <- lubridate::ymd(paste0(start_year,"-01-01"))

# start_date <- lubridate::ymd("1958-01-01")
date_seq <- seq(start_date,
    start_date + months(nrow(x_df)-1),
    by = "1 months")

x_df_ts <- x_df |>
  mutate(
    date = date_seq,
    month = tsibble::yearmonth(date)
  ) |>
  select(date, month, trend, seasonal, x_t) |> 
  as_tsibble(index = month)
Date Month Trend, $$m_t$$ Seasonal, $$s_t$$ Data, $$x_t$$
2014-01-01 2014 Jan 10.05 0.5 10.842
2014-02-01 2014 Feb 10.1 0.366 10.461
2014-03-01 2014 Mar 10.15 1 9.993
2014-04-01 2014 Apr 10.2 1.366 9.082
2014-05-01 2014 May 10.25 0.5 8.701
2014-06-01 2014 Jun 10.3 -0.5 7.697
⋮ ⋮ ⋮ ⋮ ⋮
2023-11-01 2023 Nov 15.95 -0.5 16.264
2023-12-01 2023 Dec 16 0.5 18.165

The code above has generated simulated data, where the trend is linear with equation

\[ m_t = \frac{t}{20} \]

and the seasonal effect follows the function

\[ s_t = \sin \left( \frac{t\pi}{6} \right) + \frac{1}{2}\cos\left(\frac{t \pi}{18} \right) \]

Letting \(t\) represent the month number across 10 years, we simulate a time series. Click on the tabs below to compare the actual construction of the time series (using the components generated in the code above) to the decomposition in R.

Here is a plot of the components of the simulated data.

Show the code 
trend_plot <- ggplot(x_df_ts, aes(x=month, y=trend)) + 
  geom_line() +
  labs(
    title="Plot of Trend", 
    x="Month", 
    y="Trend"
    ) +
  theme(plot.title = element_text(hjust = 0.5))

seasonal_plot <- ggplot(x_df_ts, aes(x=month, y=seasonal)) + 
  geom_line() +
  labs(
    title="Plot of Seasonal Effect", 
    x="Month", 
    y="Seasonal"
    ) +
  theme(plot.title = element_text(hjust = 0.5))

error_plot <- ggplot(x_df_ts, aes(x = month, y = x_t - trend - seasonal)) + 
  geom_line() +
  labs(
    title="Plot of Random Error Term", 
    x="Month", 
    y="Random"
  ) +
  theme(plot.title = element_text(hjust = 0.5))

x_plot <- ggplot(x_df_ts, aes(x=month, y=x_t)) + 
  geom_line() +
  labs(
    title="Plot of Simulated Time Series", 
    x="Month", 
    y="$$x_t$$"
  ) +
  theme(plot.title = element_text(hjust = 0.5))

x_plot <- x_plot  + labs(title = "True (Simulated) Values", x = NULL)
trend_plot <- trend_plot + labs(title = NULL, x = NULL)
seasonal_plot <- seasonal_plot + labs(title = NULL, x = NULL)
error_plot <- error_plot + labs(title = NULL)

x_plot / trend_plot / seasonal_plot / error_plot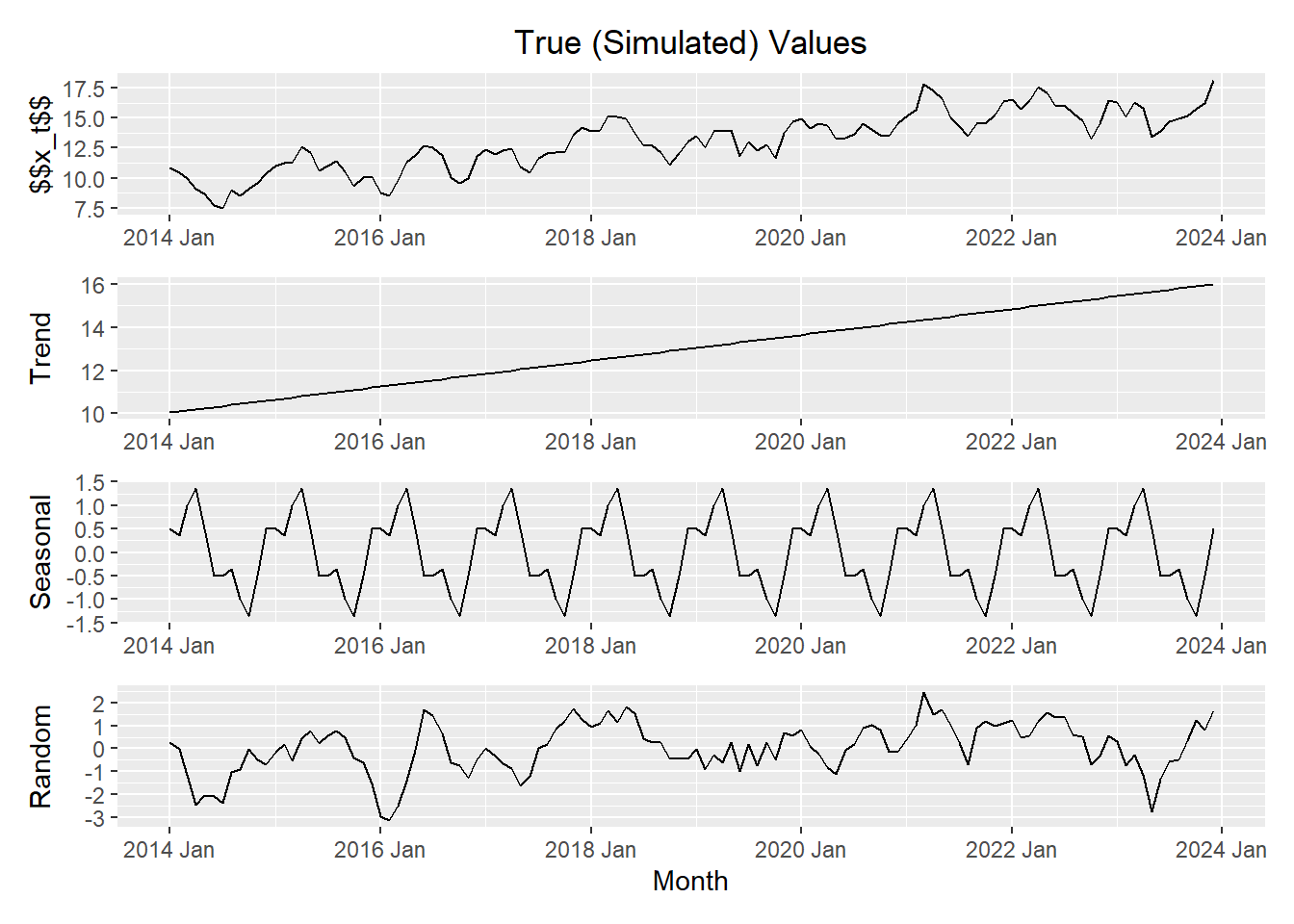

Now, we use R to decompose the time series \(\{x_t\}\).

Show the code 
x_decompose <- x_df_ts |>
    model(feasts::classical_decomposition(x_t,
        type = "add"))  |>
    components()

autoplot(x_decompose)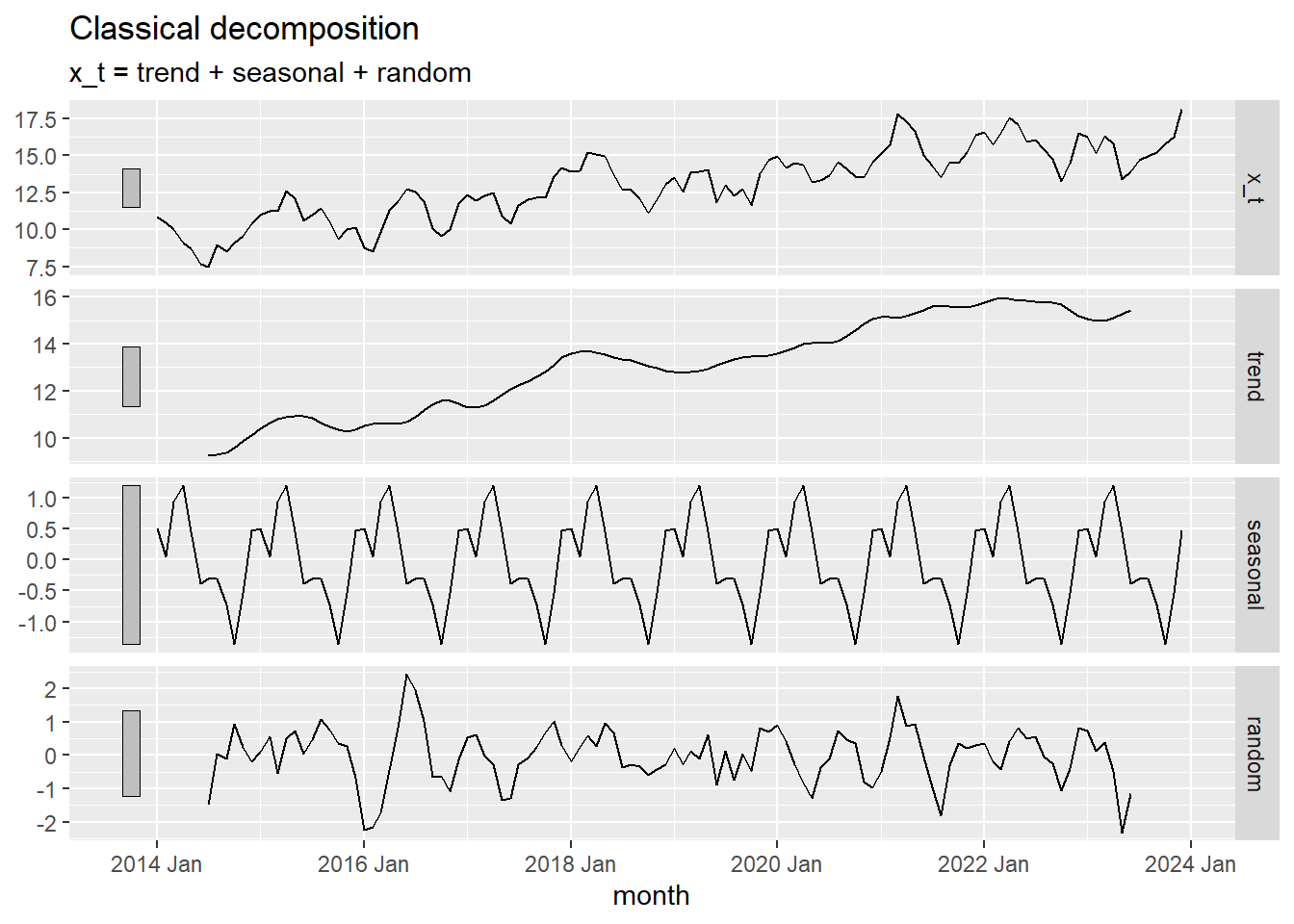

Check Your Understanding
  • How does the (estimated) decomposition compare to the theoretical values above?
    • How well is the trend estimated?
    • How well is the seasonal effect estimated?
    • How well is the random effect estimated?
  • Make changes to the simulated data and observe the effect on the plots

Multiplicative Model

We now simulate data and apply R’s multiplicative model. This implies that the error term, \(z_t\), has a mean of 1, rather than 0.

Table 2: Simulated Data (Multiplicative Model)

Show the code 
# Set random seed for reproducibility
set.seed(123) 

# Set parameters & initialize vectors
num_years <- 10
n <- 12 * num_years
sigma <- .75
a <- 0.03
b <- 1
c <- 0.5 
trend <- seasonal <- x_t <- rep(0,n)
time_seq <- seq(1,n)

# Generate correlated error terms
w <- rnorm(n + 4, 0.2, 0.1) # Changed to a mean of 1 and sd of 0.03
z = w + lead(w,1) + lead(w,2) + lead(w,3) + lead(w,4)
z  = head(z, n)

# Get date
year_seq <- lubridate::year(today()) - num_years  + (time_seq - 1) %/% 12
month_seq <- (time_seq - 1) %% 12 + 1
date_seq <- ymd(paste0(year_seq,"-",month_seq,"-01"))

# Get data
for (t in 1:n) {
  trend[t] <- exp(a * t)
  seasonal[t] <- exp( b * sin(t / 12 * 2 * pi * 1)  + c * cos(t / 12 * 2 * pi * 3) + 1 )
  x_t[t] <- trend[t] * seasonal[t] * z[t] # Note R's definition of the mult. model
}

x_df <- data.frame(x_t = x_t, trend = trend, seasonal = seasonal)

start_year <- lubridate::year(today()) - num_years
start_date <- lubridate::ymd(paste0(start_year,"-01-01"))

# start_date <- lubridate::ymd("1958-01-01")
date_seq <- seq(start_date,
    start_date + months(nrow(x_df)-1),
    by = "1 months")

x_df_ts <- x_df |>
  mutate(
    date = date_seq,
    month = tsibble::yearmonth(date)
  ) |>
  select(date, month, trend, seasonal, x_t) |>
  as_tsibble(index = month)
Date Month Trend, $$m_t$$ Seasonal, $$s_t$$ Data, $$x_t$$
2014-01-01 2014 Jan 1.03 4.482 5.065
2014-02-01 2014 Feb 1.062 3.92 5.512
2014-03-01 2014 Mar 1.094 7.389 11.266
2014-04-01 2014 Apr 1.127 10.655 13.348
2014-05-01 2014 May 1.162 4.482 5.391
2014-06-01 2014 Jun 1.197 1.649 1.93
⋮ ⋮ ⋮ ⋮ ⋮
2023-11-01 2023 Nov 35.517 1.649 39.853
2023-12-01 2023 Dec 36.598 4.482 121.366

The code above simulated data, where the trend is exponential with equation

\[ m_t = e^{0.03 t} \]

and the seasonal effect follows the function

\[ s_t = \sin \left( \frac{t\pi}{6} \right) + \frac{1}{2}\cos\left(\frac{t \pi}{18} \right) + 1 \]

Letting \(t\) represent the month number across 10 years, we simulate a time series with multiplicative effects. Click on the tabs below to compare the actual construction of the time series (using the components generated in the code above) to the decomposition in R.

Here is a plot of the components of the simulated data.

Show the code 
trend_plot <- ggplot(x_df_ts, aes(x=month, y=trend)) + 
  geom_line() +
  labs(
    title="Plot of Trend", 
    x="Month", 
    y="Trend"
    ) +
  theme(plot.title = element_text(hjust = 0.5))

seasonal_plot <- ggplot(x_df_ts, aes(x=month, y=seasonal)) + 
  geom_line() +
  labs(
    title="Plot of Seasonal Effect", 
    x="Month", 
    y="Seasonal"
    ) +
  theme(plot.title = element_text(hjust = 0.5))

error_plot <- ggplot(x_df_ts, aes(x = month, y = x_t / trend / seasonal)) + 
  geom_line() +
  labs(
    title="Plot of Random Error Term", 
    x="Month", 
    y="Random"
  ) +
  theme(plot.title = element_text(hjust = 0.5))

x_plot <- ggplot(x_df_ts, aes(x=month, y=x_t)) + 
  geom_line() +
  labs(
    title="Plot of Simulated Time Series", 
    x="Month", 
    y="x_t"
  ) +
  theme(plot.title = element_text(hjust = 0.5))

x_plot <- x_plot  + labs(title = "True (Simulated) Values", x = NULL)
trend_plot <- trend_plot + labs(title = NULL, x = NULL)
seasonal_plot <- seasonal_plot + labs(title = NULL, x = NULL)
error_plot <- error_plot + labs(title = NULL)

x_plot / trend_plot / seasonal_plot / error_plot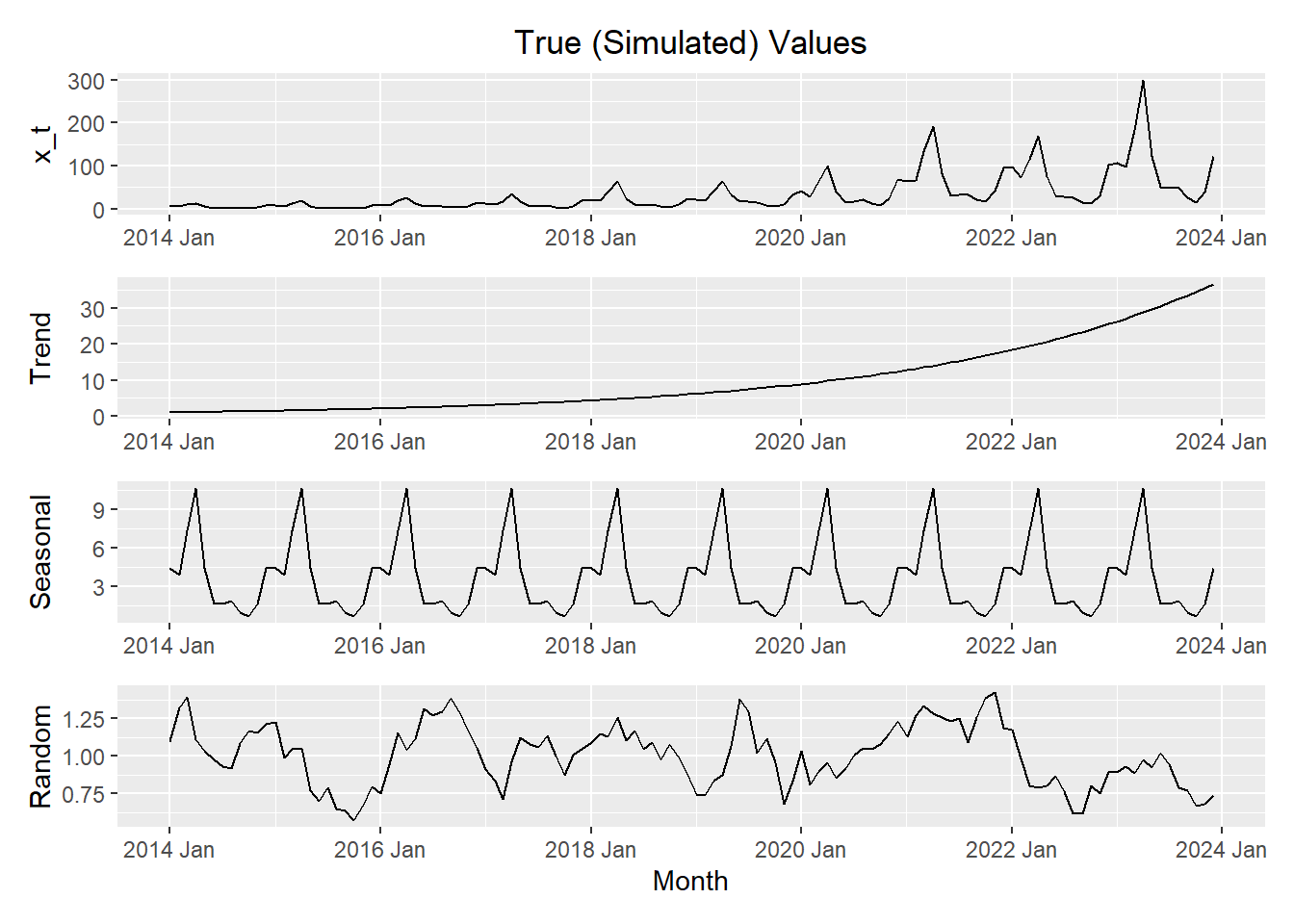

Now, we use R to decompose the time series \(\{x_t\}\).

Show the code 
x_decompose <- x_df_ts |>
    model(feasts::classical_decomposition(x_t,
        type = "mult"))  |>
    components()

autoplot(x_decompose)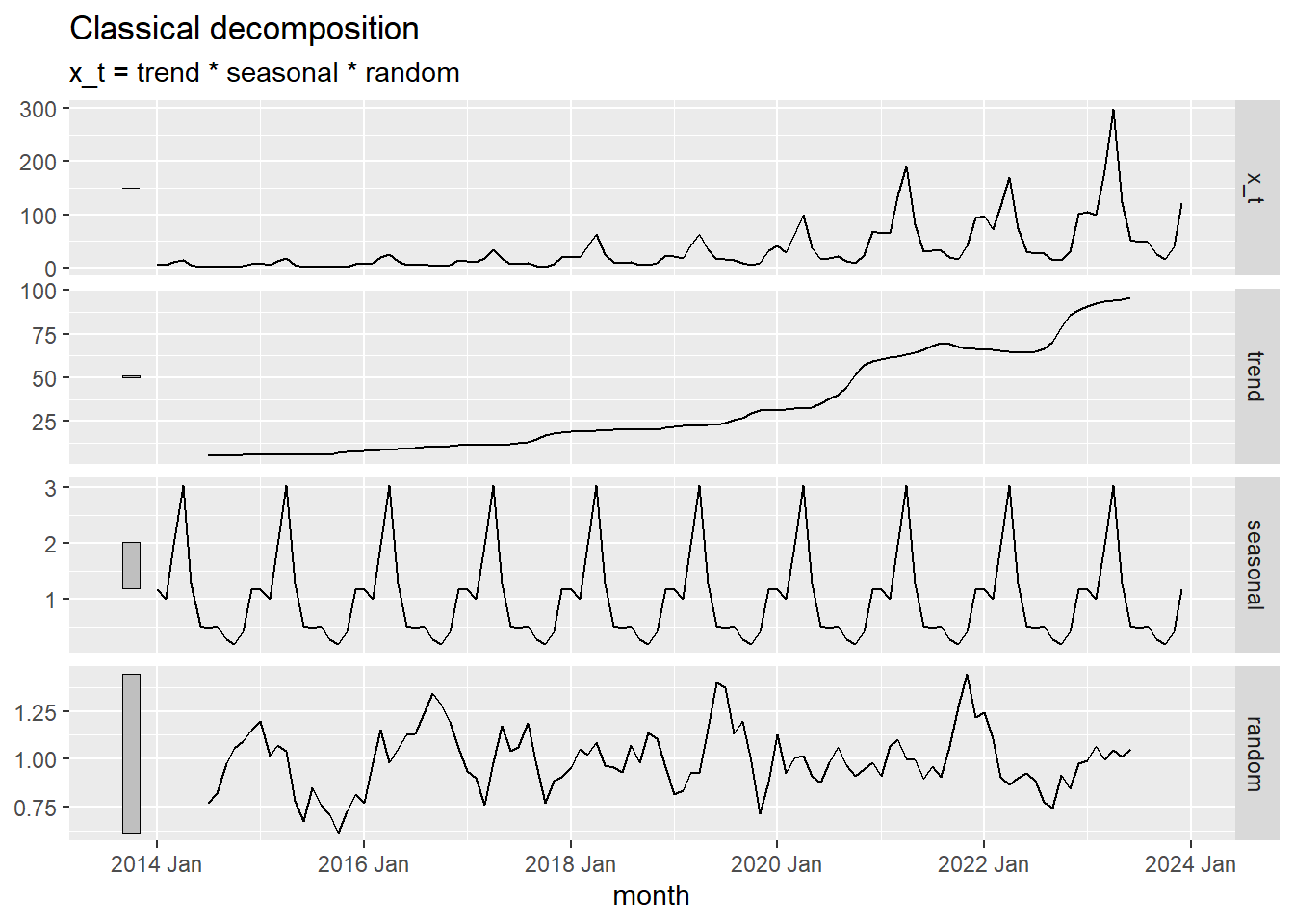

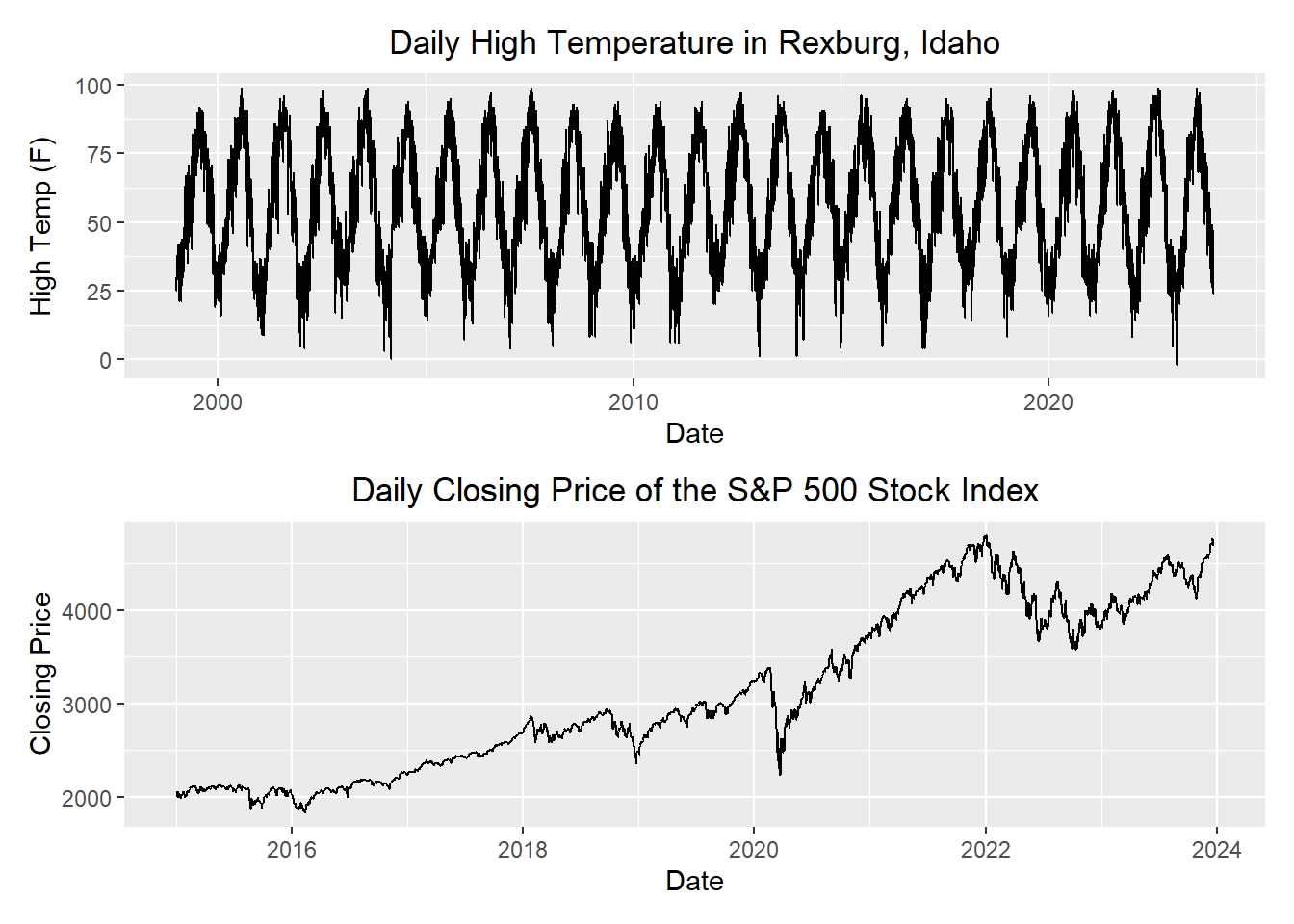
Check Your Understanding
  • How does the (estimated) decomposition compare to the theoretical values above?
    • How well is the trend estimated?
    • How well is the seasonal effect estimated?
    • How well is the random effect estimated?
  • Make changes to the simulated data and observe the effect on the plots

Which Model Should I Use: Additive or Multiplicative?

Compare the following two time series.

Check Your Understanding

Complete a table like the following in your Learning Journal to compare characteristics of these two time series. Be sure to include a sketch of the respective time plots.

Rexburg Temperature S&P 500 Closing Price
Deterministic or stochastic trend?
Is there a seasonal effect?
Is there evidence of cycles?
Does the variation get bigger over time?
Additive or multiplicative model?

Small Group Activity: Apple’s Quarterly Revenue (30 min)

The code below imports and plots the quarterly revenue for Apple Inc. (in billions of U.S. dollars).

Show the code 
apple_ts <- rio::import("https://byuistats.github.io/timeseries/data/apple_revenue.csv") |>
  mutate(
    dates = mdy(date),
    year = lubridate::year(dates),
    quarter = lubridate::quarter(dates),
    value = revenue_billions
  ) |>
  dplyr::select(dates, year, quarter, value)  |> 
  arrange(dates) |>
  mutate(index = tsibble::yearquarter(dates)) |>
  as_tsibble(index = index) |>
  dplyr::select(index, dates, year, quarter, value) |>
  rename(revenue = value) # rename value to emphasize data context

apple_ts |>
  autoplot(.vars = revenue) +
  labs(
    x = "Quarter",
    y = "Apple Revenue, Billions $US",
    title = "Apple's Quarterly Revenue, Billions of U.S. Dollars"
  ) +
  theme_minimal() +
  theme(plot.title = element_text(hjust = 0.5))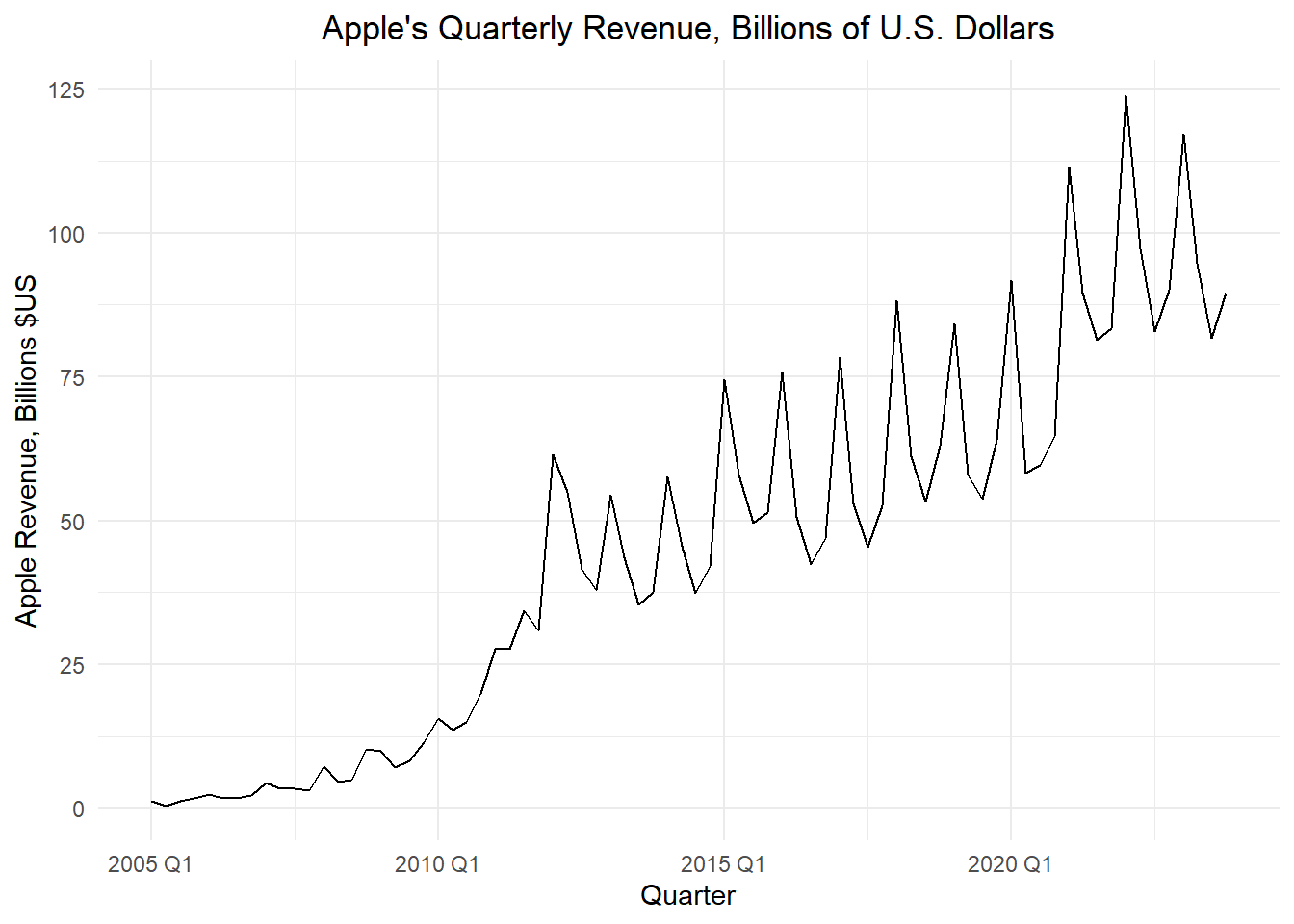

Check Your Understanding
  • What do you notice?
    • Does it seem like there is a trend in the time series?
    • Is there evidence of a seasonal effect? If so, during which quarter(s) are the revenues particularly high? particularly low?
    • Can you attribute a reason for this behavior?
  • Is an additive or multiplicative model more appropriate? Why?

We want to find the seasonally adjusted series for a multiplicative model. This is a multi-step process.

Centered Moving Average

First, we compute the centered moving average, \(\hat m_t\).

Check Your Understanding
  • Write a mutate statement that will compute the 4-quarter moving average for the variable “revenue” in the tsibble apple_ts. You can use the mutate statement from Chapter 1 Lesson 4 as a starting point.
# computes the 4-quarter centered moving average (m_hat)
apple_ts <- apple_ts |> 
  mutate(
    m_hat = 
      # Your code goes here
  )

To emphasize the computation of the centered moving average, the observed data values that were used to find \(\hat m_t\) for the first quarter of 2007 are shown in green in the table below.

Estimated Quarterly Multiplicative Effect

The centered moving average, \(\hat m_t\), is then used to compute the quarterly multiplictive effect, \(\hat s_t\):

\[ \hat s_t = \dfrac{ x_t }{ \hat m_t } \]

Table 3: Computation of the Centered Moving Average, \(\hat m_t\), and the Estimated Quarterly Multiplicative Effect, \(\hat s_t\)

quarter Revenue $$x_t$$ $$ \hat m_t $$ $$ \hat s_t $$
2005 Q1 1.24 NA ______
2005 Q2 0.48 NA ______
2005 Q3 1.24 1.315 ______
2005 Q4 1.71 ______ ______
2006 Q1 2.42 1.829 ______
2006 Q2 1.71 ______ ______
2006 Q3 1.71 2.251 ______
2006 Q4 2.19 ______ 0.808
2007 Q1 4.37 3.136 1.393
2007 Q2 3.42 3.469 0.986
2007 Q3 3.42 3.956 0.864
2007 Q4 3.14 4.474 0.702
2008 Q1 7.32 4.801 1.525
2008 Q2 4.61 5.87 0.785
⋮ ⋮ ⋮ ⋮
2022 Q4 90.146 96.579 0.933
2023 Q1 117.154 96.128 1.219
2023 Q2 94.836 95.902 0.989
2023 Q3 81.797 NA NA
2023 Q4 89.498 NA NA
Check Your Understanding
  • Working with your assigned partner, fill in the missing values of \(\hat m_t\) in the table above.
  • Then, find the missing values of \(\hat s_t\).

Seasonally Adjusted Factors

Next, we need to compute the mean (across years) of \(\hat s_t\) by quarter. To help us calculate this, it can be convenient to organize the values of \(\hat s_t\) in a table, where the rows give the year and the columns give the quarter.

The overall mean of these means will be reasonably close to, but not exactly one. We adjust these values by dividing the quarterly means by the overall mean.

Table 4: Computation of the Seasonally Adjusted Factors, \(\bar s_t\)

Year Q1 Q2 Q3 Q4
2005 NA NA ______ ______
2006 ______ ______ ______ 0.808
2007 1.393 0.986 0.864 0.702
2008 1.525 0.785 0.683 1.325
2009 1.182 0.781 0.834 1.005
2010 1.193 0.912 0.849 0.963
2011 1.106 0.961 0.999 0.734
2012 1.328 1.141 0.865 0.828
2013 1.249 1.019 0.819 0.856
2014 1.301 1.012 0.783 0.818
2015 1.367 1.013 0.847 0.891
2016 1.355 0.928 0.781 0.855
2017 1.412 0.935 0.776 0.864
2018 1.405 0.939 0.808 0.968
2019 1.303 0.894 0.816 0.956
2020 1.356 0.851 0.84 0.835
2021 1.326 1.005 0.875 0.872
2022 1.282 0.995 0.849 0.933
2023 1.219 0.989 NA NA
Mean ______ ______ ______ ______
$$ \bar s_t $$ $$~$$ ______ $$~$$ ______ $$~$$ ______ $$~$$ ______
Check Your Understanding
  • The table above gives the values of \(\hat s_t\). Fill in the missing values in the first two rows of the table above. (Note you already computed these.)
  • The second-to-last row (labeled “Mean”) gives the values of \(\bar s_t\). Find the mean of the \(\hat s_t\) values for each quarter. Call these means \(\bar {\hat s_t}\). To simplify your computations, the sum of the values visible in the table above is summarized here:
Quarter Q1 Q2 Q3 Q4
Partial Sum 22.302 16.146 13.288 15.213
  • Compute the mean of the \(\bar {\hat s_t}\) values. Call this number \(\bar {\bar {\hat s_t}}\) (This number should be relatively close to 1.)
  • Divide each of the \(\bar {\hat s_t}\) values by \(\bar {\bar {\hat s_t}}\) to get \(\bar s_t\), the seasonally adjusted factor for quarter \(t\). (Note that the mean of the \(\bar s_t\) values will be 1.)

\[ \bar s_t = \frac{ \left( \bar {\hat s_t} \right) }{ \left( \bar {\bar {\hat s_t}} \right) } \]

Random Component and the Seasonally Adjusted Time Series

Using R’s definition of the multiplicative model, we calculate the random component by dividing the values in the time series by the product of the trend and the seasonally adjusted factor:

\[ \text{random component} = \dfrac{ x_t }{ \hat m_t \cdot \bar s_t } \]

The seasonally adjusted series is computed by dividing the respective observed values by \(\bar s_t\):

\[ \text{seasonally adjusted series} = \dfrac{ x_t }{ \bar s_t } \]

Use these equations to calculate the values missing from the table below. The adjusted seasonal effect \(\bar s_t\) (s_bar) was computed in the last row of the previous table.

Table 5: Computation of the Random Component and the Seasonally Adjusted Time Series

Quarter Revenue $$x_t$$ $$ \hat m_t $$ $$ \hat s_t $$ $$ \bar s_t $$ Random Seasonally Adjusted $$x_t$$
2005 Q1 1.24 NA ______ ______ ______ ______
2005 Q2 0.48 NA ______ ______ ______ ______
2005 Q3 1.24 1.315 ______ ______ ______ ______
2005 Q4 1.71 1.616 ______ ______ ______ ______
2006 Q1 2.42 1.829 ______ ______ ______ ______
2006 Q2 1.71 1.947 ______ ______ ______ ______
2006 Q3 1.71 2.251 ______ ______ ______ ______
2006 Q4 2.19 2.709 0.808 0.905 0.893 2.42
2007 Q1 4.37 3.136 1.393 1.314 1.06 3.325
2007 Q2 3.42 3.469 0.986 0.947 1.041 3.612
⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮

Class Activity: Computing the Multiplicative Decomposition in R (3 min)

The R code below calculates the decomposition, including the seasonally adjusted time series, beginning with the tsibble apple_ts.

Table 6: First Few Rows of the Decomposition of the Apple Revenue Time Series

Show the code 
apple_decompose <- apple_ts |>
  model(feasts::classical_decomposition(revenue,
          type = "mult"))  |>
  components()

apple_decompose |>
  head(8) |>
  display_table()
.model index revenue trend seasonal random season_adjust
feasts::classical_decomposition(revenue, type = "mult") 2005 Q1 1.24 NA 1.3141184 NA 0.9435984
feasts::classical_decomposition(revenue, type = "mult") 2005 Q2 0.48 NA 0.9469622 NA 0.5068840
feasts::classical_decomposition(revenue, type = "mult") 2005 Q3 1.24 1.31500 0.8337749 1.1309596 1.4872119
feasts::classical_decomposition(revenue, type = "mult") 2005 Q4 1.71 1.61625 0.9051445 1.1688792 1.8892010
feasts::classical_decomposition(revenue, type = "mult") 2006 Q1 2.42 1.82875 1.3141184 1.0069932 1.8415388
feasts::classical_decomposition(revenue, type = "mult") 2006 Q2 1.71 1.94750 0.9469622 0.9272269 1.8057743
feasts::classical_decomposition(revenue, type = "mult") 2006 Q3 1.71 2.25125 0.8337749 0.9110109 2.0509132
feasts::classical_decomposition(revenue, type = "mult") 2006 Q4 2.19 2.70875 0.9051445 0.8932176 2.4195031
Show the code 
autoplot(apple_decompose)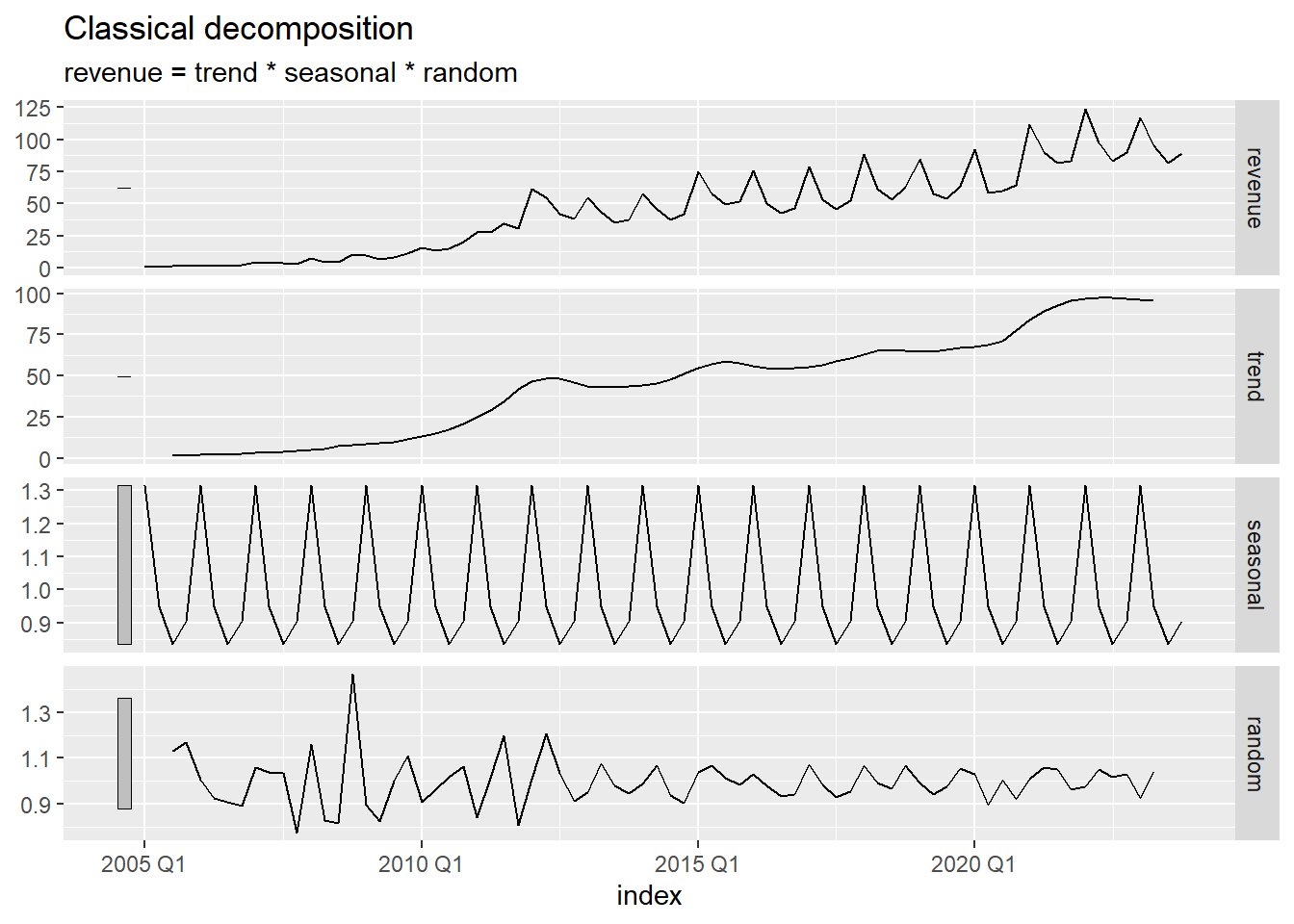

The figure below illustrates the original time series (in black), the centered moving average \(\hat m_t\) (in blue), and the seasonally adjusted series (in red).

Show the code 
apple_decompose |>
  ggplot() +
  geom_line(data = apple_decompose, aes(x = index, y = revenue), color = "black") +
  geom_line(data = apple_decompose, aes(x = index, y = season_adjust), color = "#D55E00") +
  geom_line(data = apple_decompose, aes(x = index, y = trend), color = "#0072B2") +
  labs(
    x = "Quarter",
    y = "Quarterly Revenue, Billions",
    title = "Apple Inc. Quarterly Revenue (in Billions of U.S. Dollars)"
  ) +
  theme(plot.title = element_text(hjust = 0.5))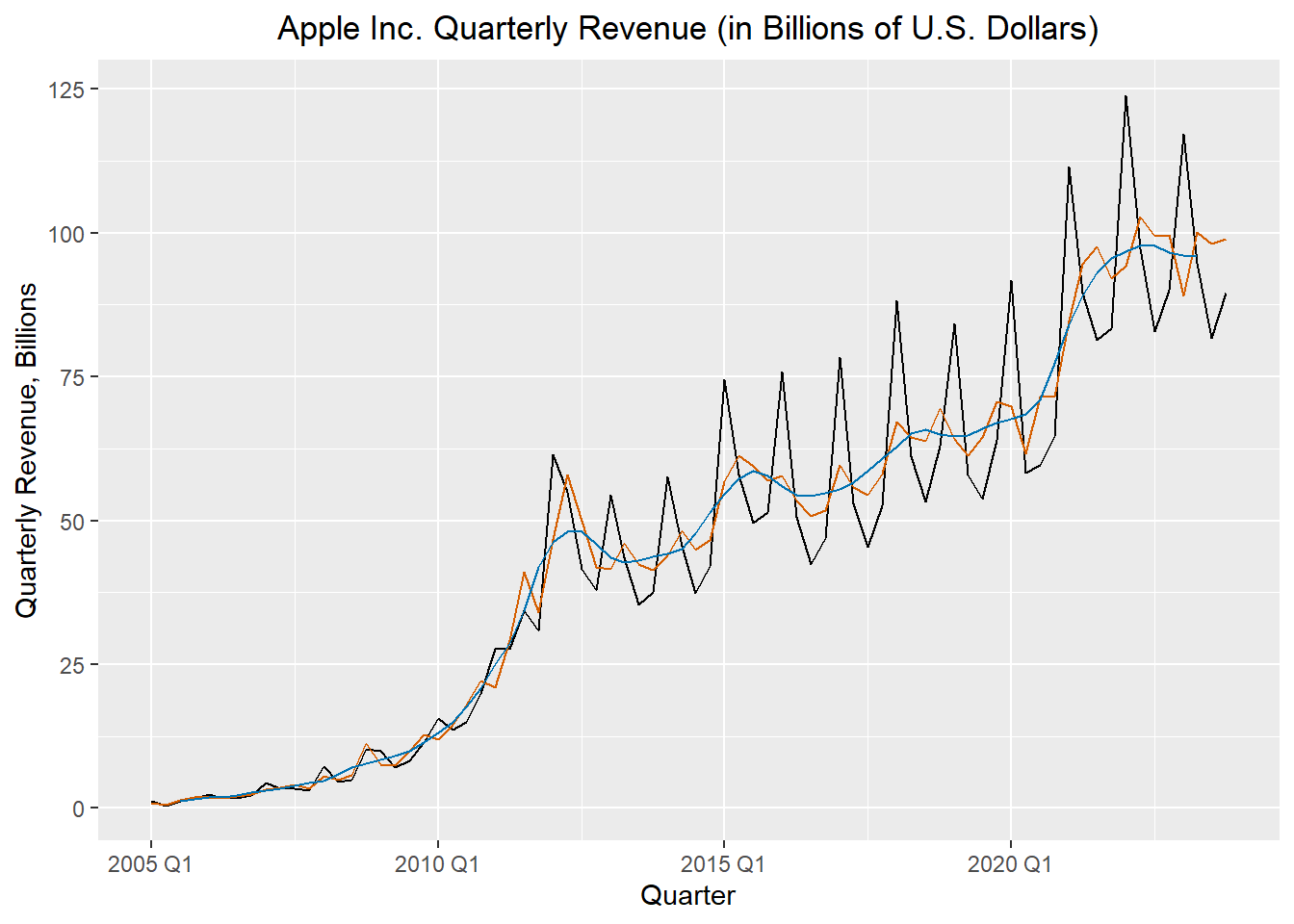

Check Your Understanding
  • Do you observe a trend in the time series?
    • What does this trend suggest?
  • In what quarter does Apple tend to have the greatest revenue?
    • What would explain this phenomenon?

Homework Preview (5 min)

  • Review upcoming homework assignment
  • Clarify questions

Homework

Download Assignment

homework_1_5.qmd

Tables-Handout-Excel

Moving Average

Handout + Tables 4 and 5