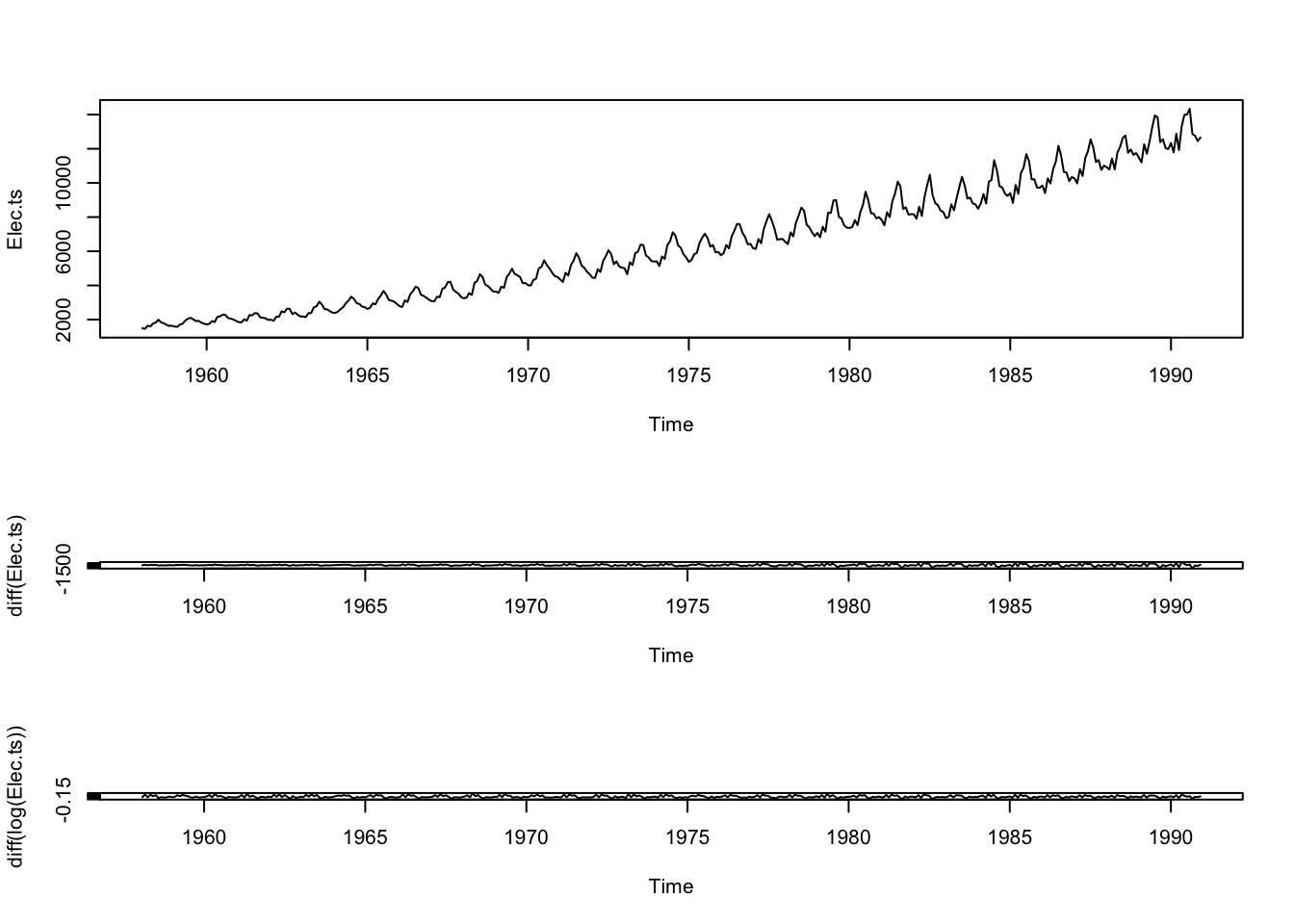
Chapter 7: Non-stationary Models

In this chapter, we extend the random walk model to include autoregressive and moving average terms. As the differenced series needs to be ‘integrated’ to recover the original series, the underlying stochastic process is called autoregressive integrated moving average, abbreviated to ARIMA.

We would like to note that the use of the R package tseries for GARCH models appears to be inferior with the addition of the rugarch package (see paper). Currently, no tidyverse developed package supports GARCH.

A short introduction to the rugarch package is helpful to discover more uses of the package.

7.2.1 “Differencing and the electricity series” Modern Look

Book code

CBE <- read.table("data/cbe.dat", header = T)
Elec.ts <- ts(CBE[, 3], start = 1958, freq = 12)
layout(c(1, 1, 2, 3))
plot(Elec.ts)
plot(diff(Elec.ts))
plot(diff(log(Elec.ts)))

Tidyverts code

pacman::p_load("tsibble", "fable", "feasts",
    "tsibbledata", "fable.prophet",
    "tidyverse", "patchwork")
cbe <- read_table("data/cbe.dat")

elec_ts <- cbe |>
  select(elec) |>
  mutate(
    date = seq(
      ymd("1958-01-01"),
      by = "1 months",
      length.out = n()),
      year_month = tsibble::yearmonth(date)) |>
  as_tsibble(index = year_month)

elec_ts |>
  mutate(
    `Diff series` = elec - lag(elec),
    `Diff log-series` = log(elec) - lag(log(elec))) |>
  pivot_longer(
    cols = all_of(c("elec", "Diff series", "Diff log-series"))) |>
  mutate(name = factor(name, levels =c("elec","Diff series", "Diff log-series"))) |>
  ggplot(aes(x = date, y = value)) +
  geom_line() +
  facet_wrap(~name, ncol = 1, scales = "free", strip.position = "left") +
  labs(x = "Time", y = "") +
  scale_x_date(breaks = "5 years", date_labels = "%Y") +
  theme_bw()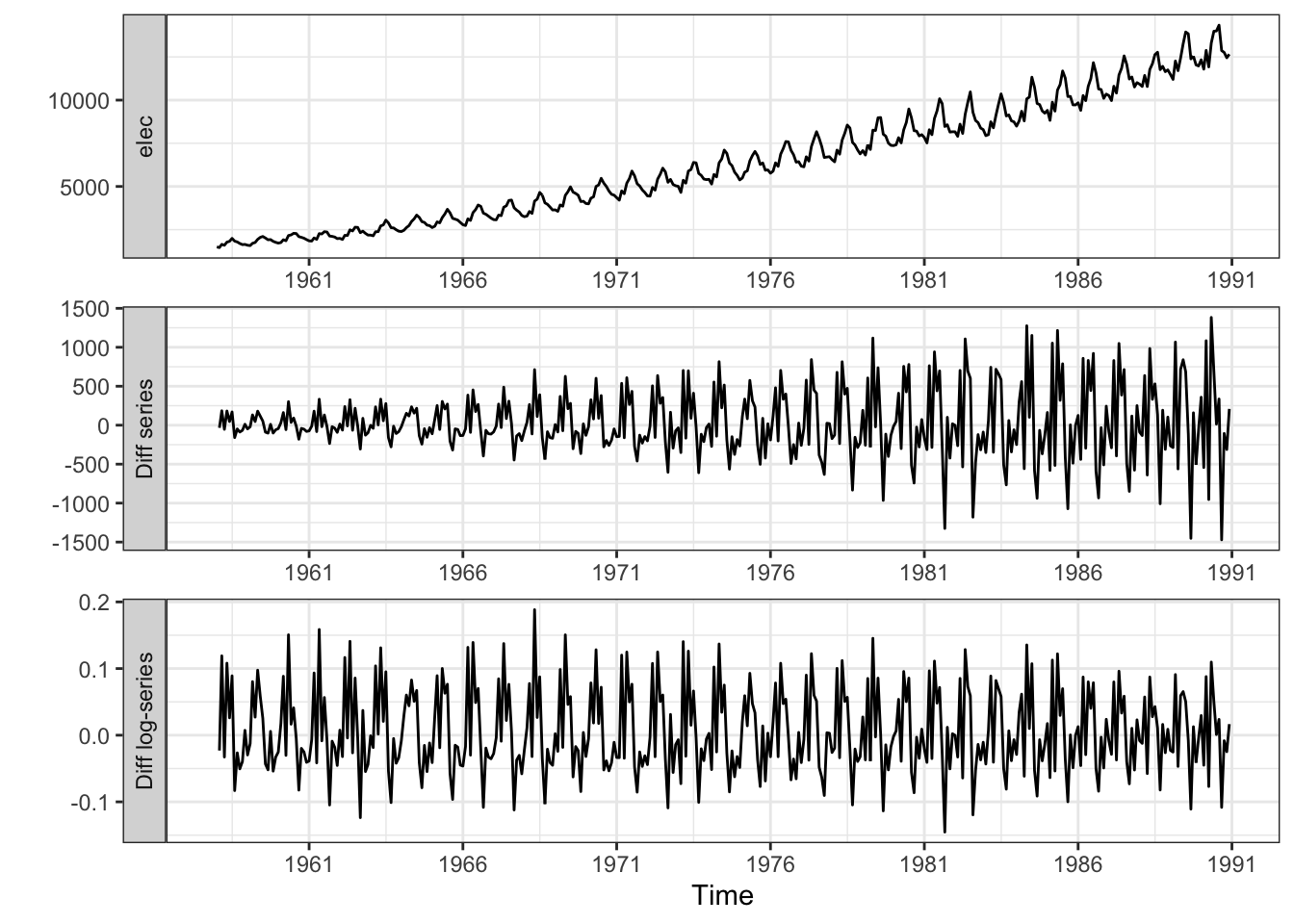

Show the Book code in full 
CBE <- read.table("data/cbe.dat", header = T)
Elec.ts <- ts(CBE[, 3], start = 1958, freq = 12)
layout(c(1, 1, 2, 3))
plot(Elec.ts)
plot(diff(Elec.ts))
plot(diff(log(Elec.ts)))
Show the Tidyverts code in full 
pacman::p_load("tsibble", "fable", "feasts",
    "tsibbledata", "fable.prophet",
    "tidyverse", "patchwork")
cbe <- read_table("data/cbe.dat")
elec_ts <- cbe |>
  select(elec) |>
  mutate(
    date = seq(
      ymd("1958-01-01"),
      by = "1 months",
      length.out = n()),
      year_month = tsibble::yearmonth(date)) |>
  as_tsibble(index = year_month)

elec_ts |>
  mutate(
    `Diff series` = elec - lag(elec),
    `Diff log-series` = log(elec) - lag(log(elec))) |>
  pivot_longer(
    cols = all_of(c("elec", "Diff series", "Diff log-series"))) |>
  mutate(name = factor(name, levels =c("elec","Diff series", "Diff log-series"))) |>
  ggplot(aes(x = date, y = value)) +
  geom_line() +
  facet_wrap(~name, ncol = 1, scales = "free", strip.position = "left") +
  labs(x = "Time", y = "") +
  scale_x_date(breaks = "5 years", date_labels = "%Y") +
  theme_bw()

7.2.4 “Simulating and fitting” Modern Look

Book code

set.seed(1)
x <- w <- rnorm(1000)
for (i in 3:1000) x[i] <- 0.5 * x[i - 1] + x[i - 1] -
  0.5 * x[i - 2] + w[i] + 0.3 * w[i - 1]
arima(x, order = c(1, 1, 1))

Call:
arima(x = x, order = c(1, 1, 1))

Coefficients:
         ar1     ma1
      0.4235  0.3308
s.e.  0.0433  0.0450

sigma^2 estimated as 1.067:  log likelihood = -1450.13,  aic = 2906.26

Tidyverts code

set.seed(1)
x <- w <- rnorm(1000)
for (i in 3:1000) x[i] <- 0.5 * x[i - 1] + x[i - 1] -
  0.5 * x[i - 2] + w[i] + 0.3 * w[i - 1]
tibble(x = x) |>
  mutate(time = 1:n()) |>
  as_tsibble(index = time) |>
  model(arima = ARIMA(x ~ pdq(1, 1, 1) + PDQ(0, 0, 0))) |>
  tidy()
# A tibble: 2 × 6
  .model term  estimate std.error statistic  p.value
  <chr>  <chr>    <dbl>     <dbl>     <dbl>    <dbl>
1 arima  ar1      0.423    0.0433      9.79 1.11e-21
2 arima  ma1      0.331    0.0450      7.35 4.02e-13
x <- arima.sim(model = list(
    order = c(1, 1, 1),
    ar = 0.5,
    ma = 0.3),
    n = 1000)
arima(x, order = c(1, 1, 1))

Call:
arima(x = x, order = c(1, 1, 1))

Coefficients:
         ar1     ma1
      0.5567  0.2502
s.e.  0.0372  0.0437

sigma^2 estimated as 1.079:  log likelihood = -1457.45,  aic = 2920.91
tibble(x = arima.sim(model = list(
    order = c(1, 1, 1),
    ar = 0.5,
    ma = 0.3),
    n = 1000)) |>
  mutate(time = 1:n()) |>
  as_tsibble(index = time) |>
  model(arima = ARIMA(x ~ pdq(1, 1, 1) + PDQ(0, 0, 0))) |>
  tidy()
# A tibble: 2 × 6
  .model term  estimate std.error statistic  p.value
  <chr>  <chr>    <dbl>     <dbl>     <dbl>    <dbl>
1 arima  ar1      0.475    0.0380     12.5  2.42e-33
2 arima  ma1      0.376    0.0395      9.53 1.19e-20
Show the Book code in full 
set.seed(1)
x <- w <- rnorm(1000)
for (i in 3:1000) x[i] <- 0.5 * x[i - 1] + x[i - 1] - 0.5 *
  x[i - 2] + w[i] + 0.3 * w[i - 1]
arima(x, order = c(1, 1, 1))
Show the Tidyverts code in full 
set.seed(1)
x <- w <- rnorm(1000)
for (i in 3:1000) x[i] <- 0.5 * x[i - 1] + x[i - 1] -
  0.5 * x[i - 2] + w[i] + 0.3 * w[i - 1]
tibble(x = x) |>
  mutate(time = 1:n()) |>
  as_tsibble(index = time) |>
  model(arima = ARIMA(x ~ pdq(1, 1, 1) + PDQ(0, 0, 0))) |>
  tidy()

tibble(x = arima.sim(model = list(
    order = c(1, 1, 1),
    ar = 0.5,
    ma = 0.3),
    n = 1000)) |>
  mutate(time = 1:n()) |>
  as_tsibble(index = time) |>
  model(arima = ARIMA(x ~ pdq(1, 1, 1) + PDQ(0, 0, 0))) |>
  tidy()

7.2.5 “IMA(1, 1) model fitted to the beer production series” Modern Look

Book code

Beer.ts <- ts(CBE[, 2], start = 1958, freq = 12)
Beer.ima <- arima(Beer.ts, order = c(0, 1, 1))
Beer.ima

Call:
arima(x = Beer.ts, order = c(0, 1, 1))

Coefficients:
          ma1
      -0.3334
s.e.   0.0558

sigma^2 estimated as 360.4:  log likelihood = -1723.27,  aic = 3450.53

Tidyverts code

cbe <- read_table("data/cbe.dat")
beer_ts <- cbe |>
  select(beer) |>
  mutate(
    date = seq(
      ymd("1958-01-01"),
      by = "1 months",
      length.out = n()),
      year_month = tsibble::yearmonth(date)) |>
  as_tsibble(index = year_month)

beer_arima <- beer_ts |>
  model(arima = ARIMA(beer ~ pdq(0, 1, 1) + PDQ(0, 0, 0)))

tidy(beer_arima)
# A tibble: 1 × 6
  .model term  estimate std.error statistic       p.value
  <chr>  <chr>    <dbl>     <dbl>     <dbl>         <dbl>
1 arima  ma1     -0.333    0.0558     -5.97 0.00000000515
acf(resid(Beer.ima))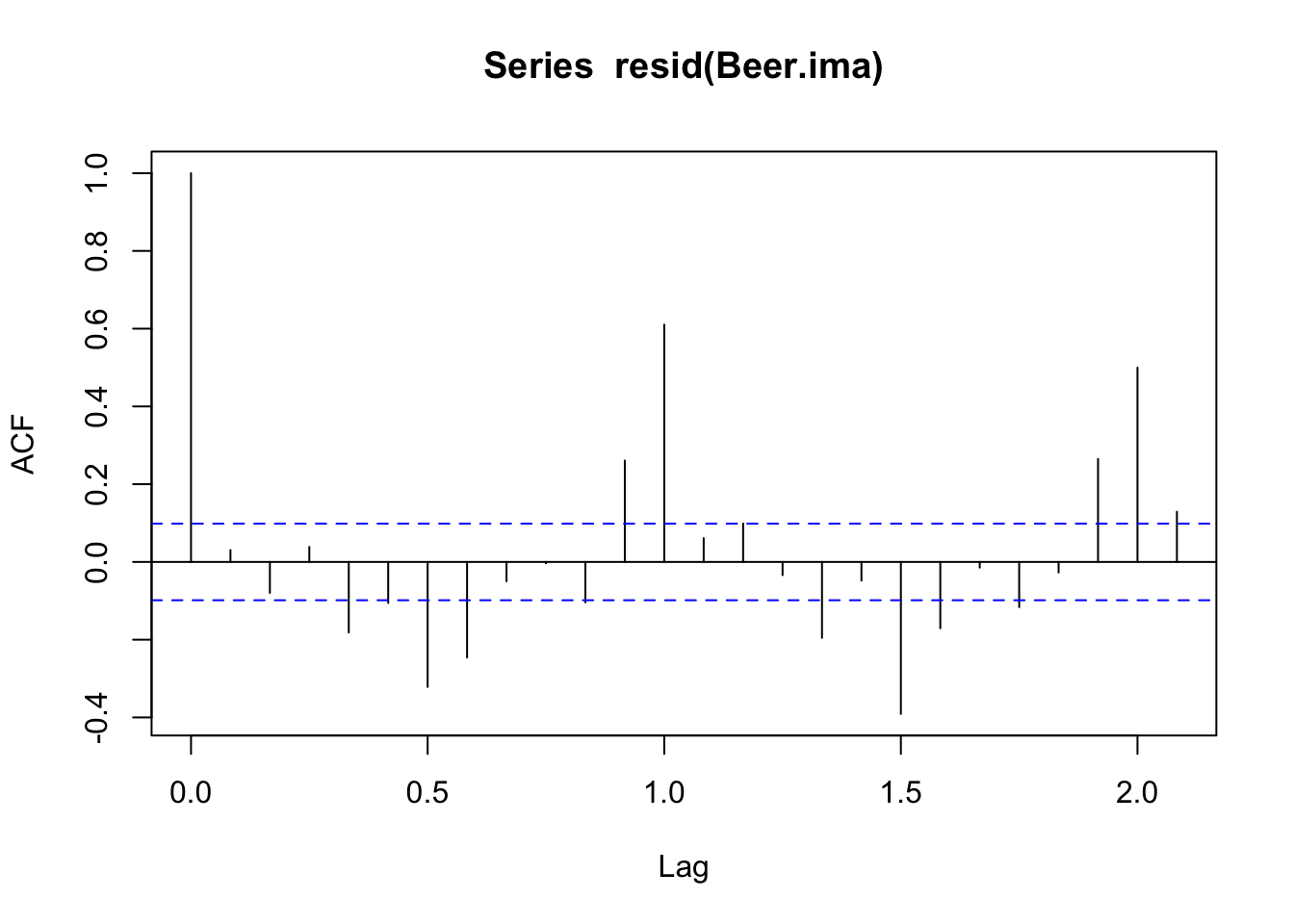

beer_arima |>
  residuals() |>
  ACF() |>
  autoplot()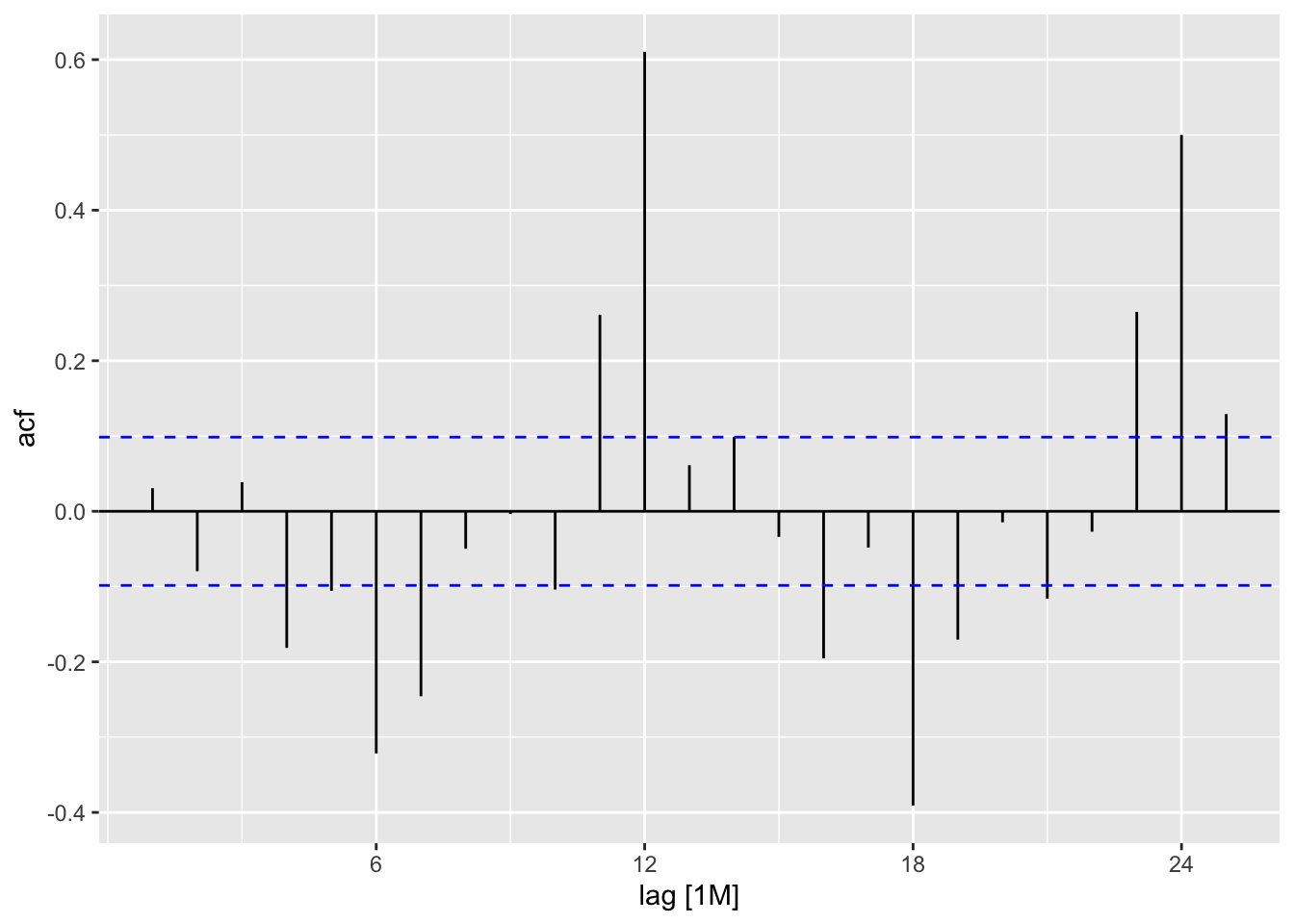

Beer.1991 <- predict(Beer.ima, n.ahead = 12)
sum(Beer.1991$pred)
[1] 2365.412
beer_1991 <- beer_arima |>
  forecast(h = "12 months")

pull(beer_1991, .mean) |> sum()
[1] 2365.412
Show the Book code in full 
Beer.ts <- ts(CBE[, 2], start = 1958, freq = 12)
Beer.ima <- arima(Beer.ts, order = c(0, 1, 1))
Beer.ima
acf(resid(Beer.ima))
Beer.1991 <- predict(Beer.ima, n.ahead = 12)
sum(Beer.1991$pred)
Show the Tidyverts code in full 
cbe <- read_table("data/cbe.dat")
beer_ts <- cbe |>
  select(beer) |>
  mutate(
    date = seq(
      ymd("1958-01-01"),
      by = "1 months",
      length.out = n()),
      year_month = tsibble::yearmonth(date)) |>
  as_tsibble(index = year_month)

beer_arima <- beer_ts |>
  model(arima = ARIMA(beer ~ pdq(0, 1, 1) + PDQ(0, 0, 0)))

tidy(beer_arima)

beer_arima |>
  residuals() |>
  ACF() |>
  autoplot()

beer_1991 <- beer_arima |>
  forecast(h = "12 months")

pull(beer_1991, .mean) |> sum()

7.3.2 “Fitting Procedure” Modern Look

Book code

aic1 <- AIC(arima(log(Elec.ts),
  order = c(1,1,0),
  seas = list(order = c(1,0,0), 12)))
aic2 <- AIC(arima(log(Elec.ts),
  order = c(0,1,1),
  seas = list(order = c(0,0,1), 12)))
c("aic1" = aic1, "aic2" = aic2)
     aic1      aic2 
-1764.741 -1361.586

Tidyverts code

elec_ts |>
  model(
    ar_model = ARIMA(log(elec) ~ 1 +
      pdq(1, 1, 0) +
      PDQ(1, 0, 0)),
    ma_model = ARIMA(log(elec) ~ 1 + 
      pdq(0, 1, 1) +
      PDQ(0, 0, 1))) |>
  glance() |> 
  pull(AIC)
[1] -1763.076 -1362.217
get.best.arima <- function(x.ts, maxord = c(1,1,1,1,1,1)) {
   best.aic <- 1e8
   n <- length(x.ts)
   for (p in 0:maxord[1]) for(d in 0:maxord[2]) for(q in 0:maxord[3])
     for (P in 0:maxord[4]) for(D in 0:maxord[5]) for(Q in 0:maxord[6])
     {
        fit <- arima(x.ts, order = c(p,d,q),
                           seas = list(order = c(P,D,Q),
                           frequency(x.ts)), method = "CSS")
        fit.aic <- -2 * fit$loglik + (log(n) + 1) * length(fit$coef)
        if (fit.aic < best.aic)
        {
          best.aic <- fit.aic
          best.fit <- fit
          best.model <- c(p,d,q,P,D,Q)
        }
      }
   list(best.aic, best.fit, best.model)
 }

best.arima.elec <- get.best.arima(
  log(Elec.ts),
  maxord = c(2,2,2,2,2,2))

best.fit.elec <- best.arima.elec[[2]]
acf(resid(best.fit.elec))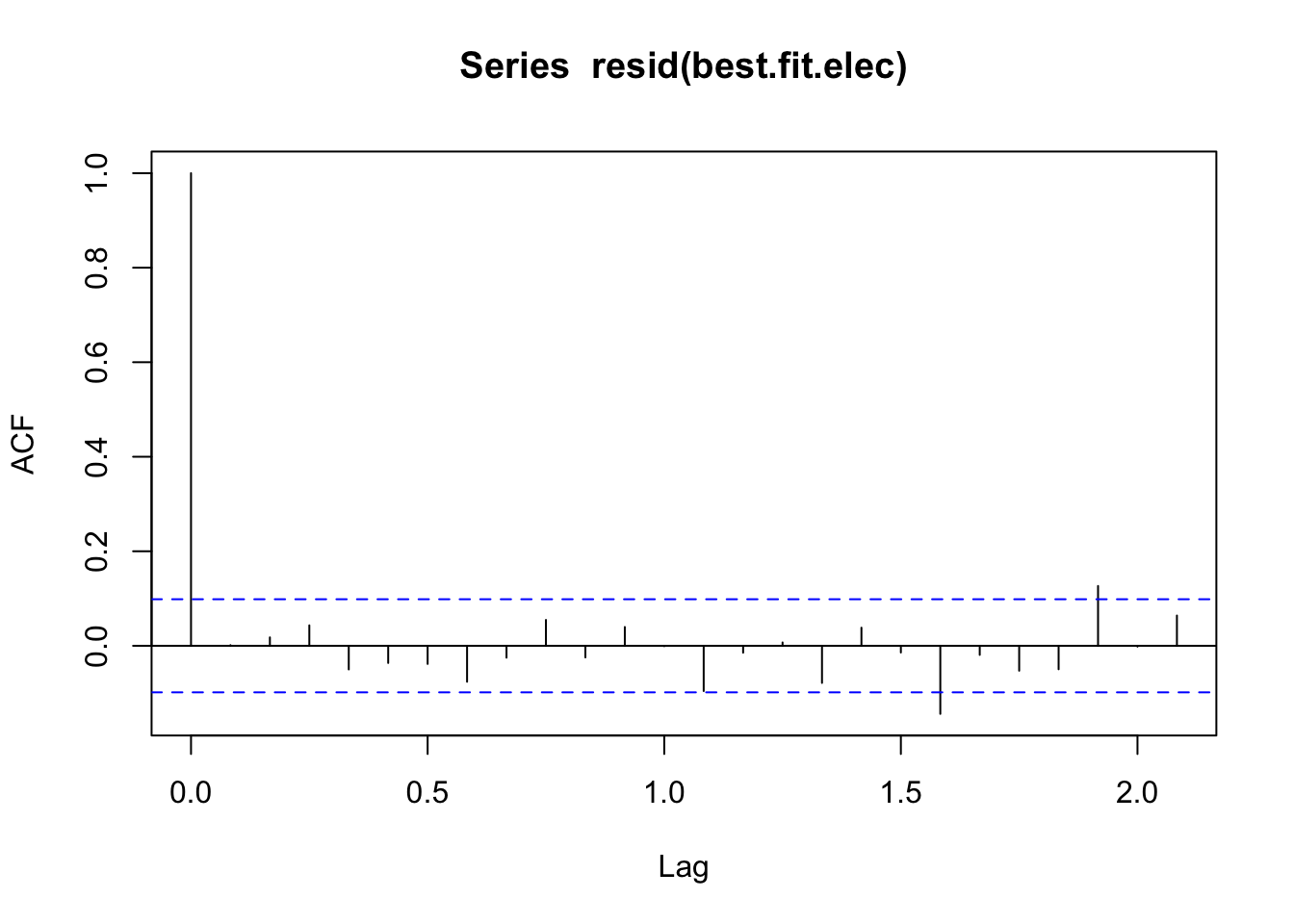

best_fit_elec <- elec_ts |>
  model(
    ar_model = ARIMA(log(elec) ~ 1 +
      pdq(0:2, 0:2, 0:2) +
      PDQ(0:2, 0:2, 0:2), approximation = TRUE))

best_fit_elec |>
  residuals() |>
  ACF() |>
  autoplot()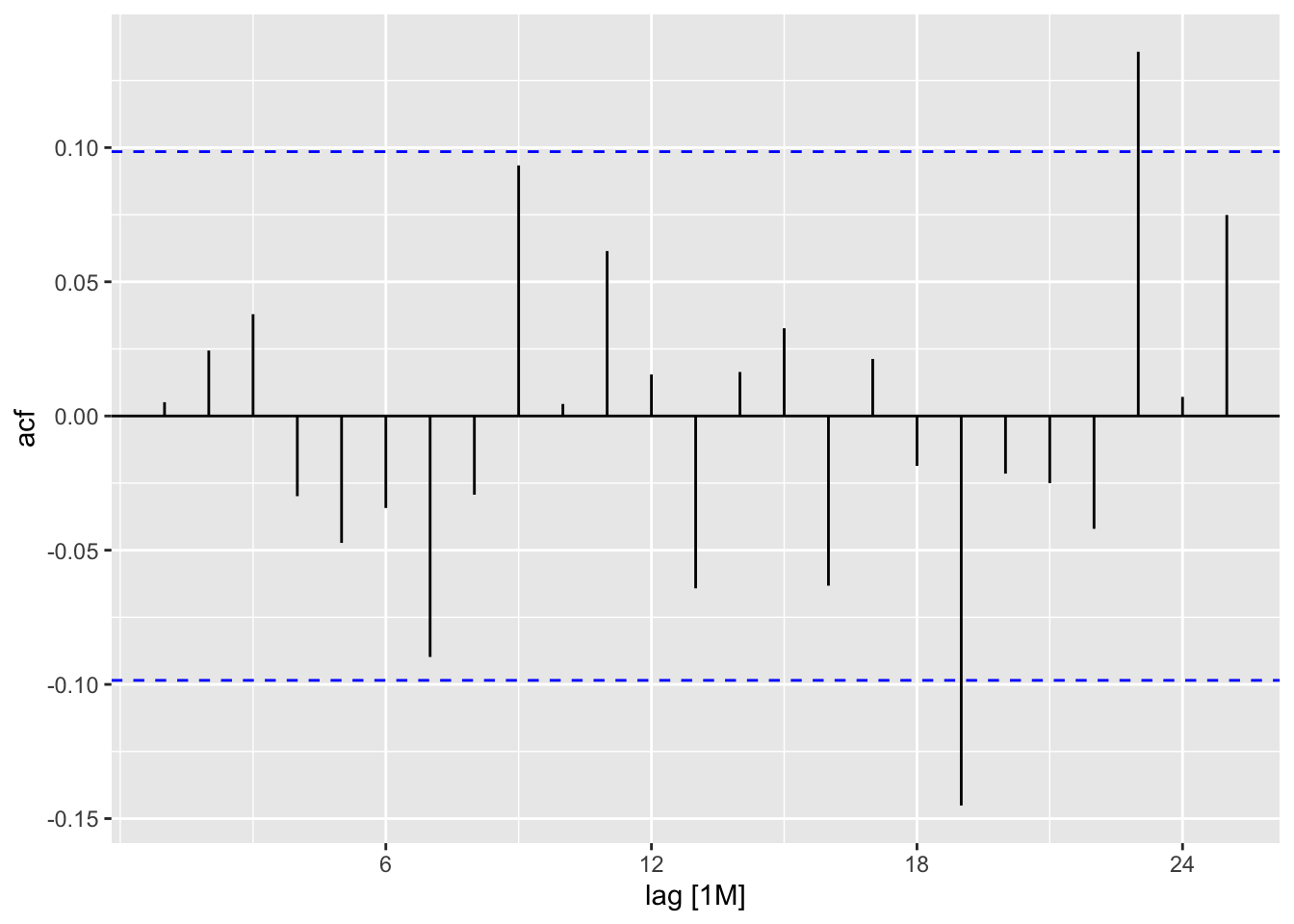

best.arima.elec[[3]]
[1] 0 1 1 2 0 2
best_fit_elec
# A mable: 1 x 1
                            ar_model
                             <model>
1 <ARIMA(2,0,1)(1,1,2)[12] w/ drift>
ts.plot(cbind(window(Elec.ts,start = 1981),
  exp(predict(best.fit.elec,12)$pred) ), lty = 1:2)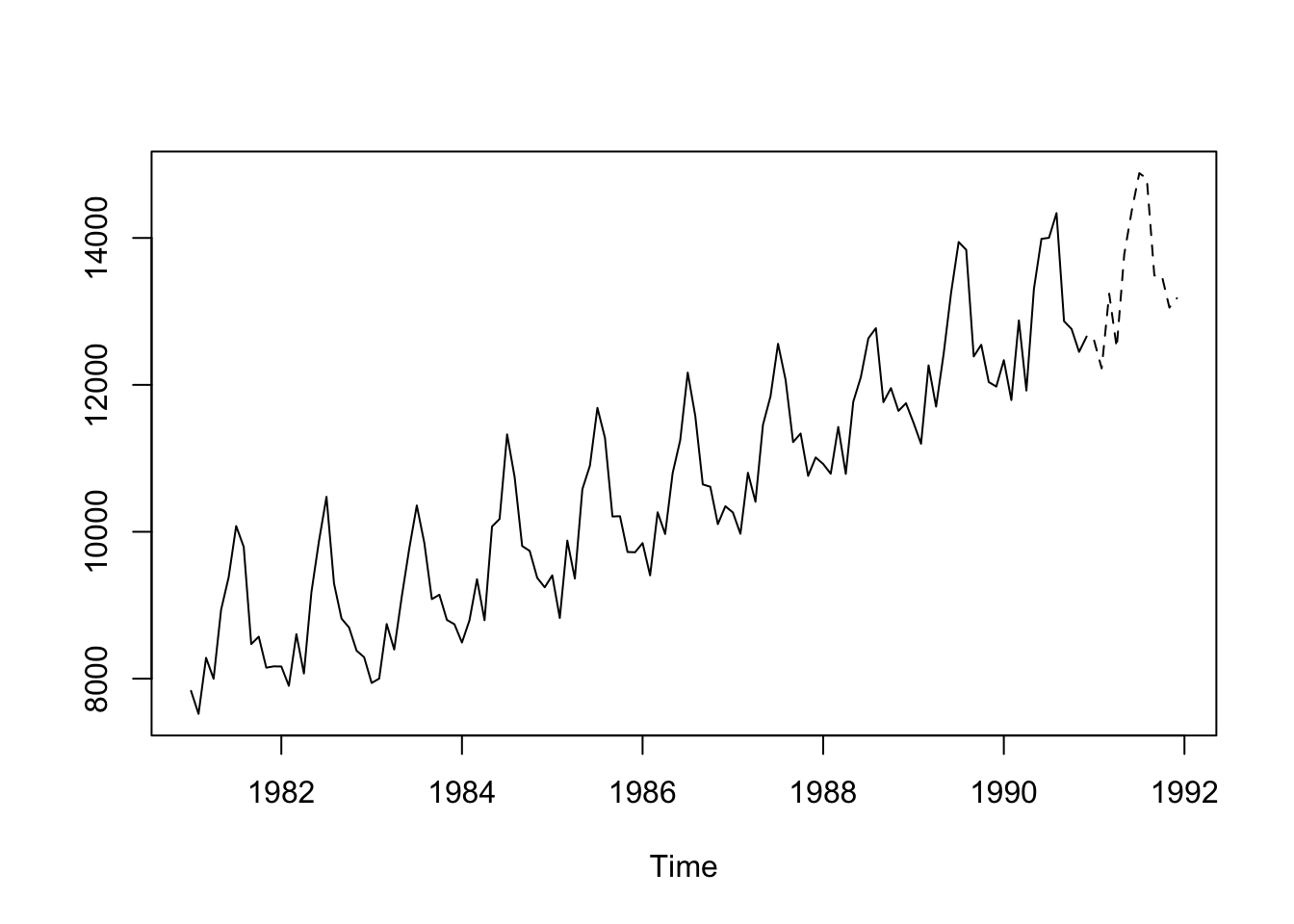

best_fit_elec |>
  forecast(h = "12 months") |>
  autoplot(filter(elec_ts, date > ymd("1981-01-01")))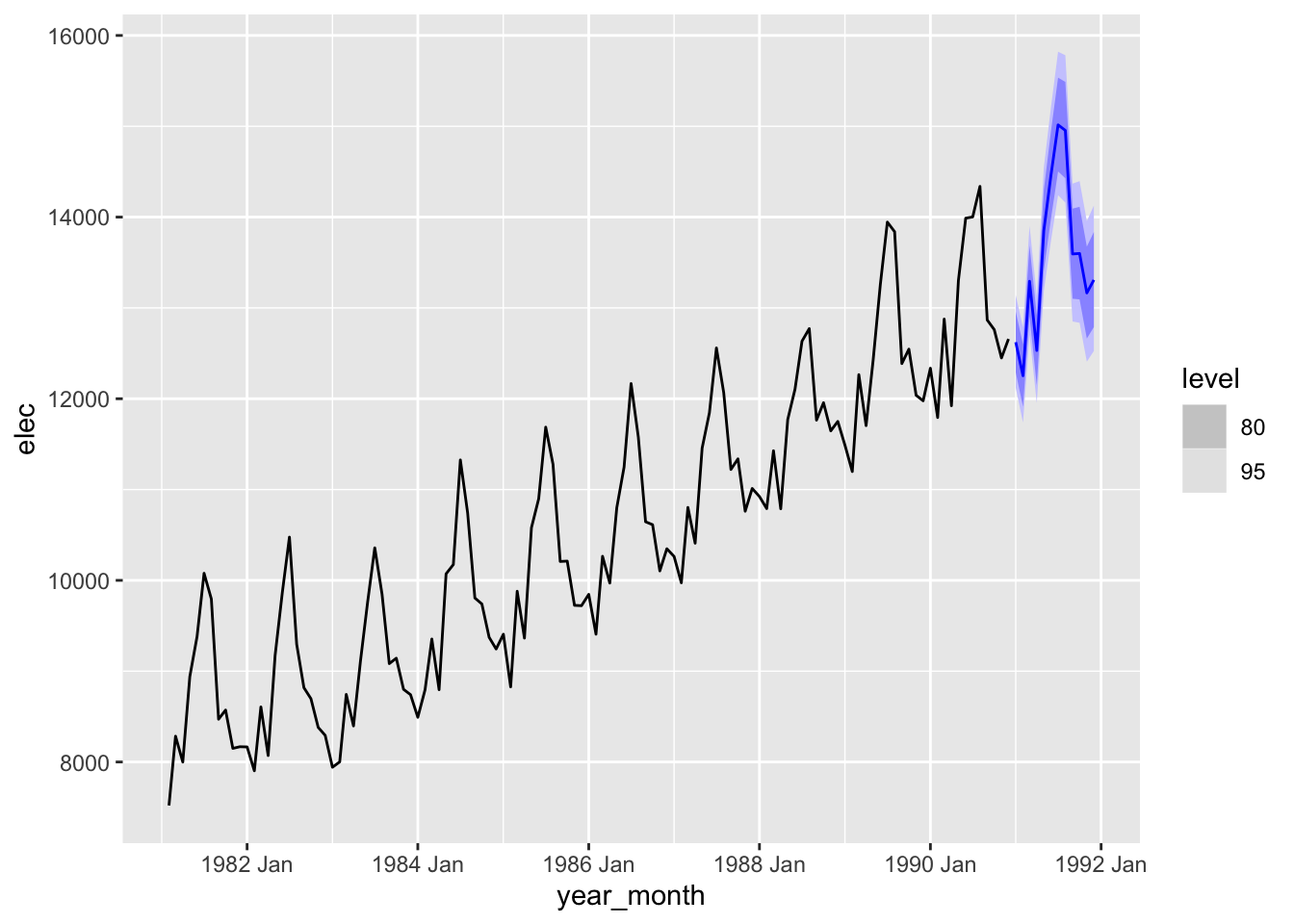

Show the Book code in full 
aic1 <- AIC(arima(log(Elec.ts),
  order = c(1,1,0),
  seas = list(order = c(1,0,0), 12)))
aic2 <- AIC(arima(log(Elec.ts),
  order = c(0,1,1),
  seas = list(order = c(0,0,1), 12)))
c("aic1" = aic1, "aic2" = aic2)
get.best.arima <- function(x.ts, maxord = c(1,1,1,1,1,1)) {
   best.aic <- 1e8
   n <- length(x.ts)
   for (p in 0:maxord[1]) for(d in 0:maxord[2]) for(q in 0:maxord[3])
     for (P in 0:maxord[4]) for(D in 0:maxord[5]) for(Q in 0:maxord[6])
     {
        fit <- arima(x.ts, order = c(p,d,q),
                           seas = list(order = c(P,D,Q),
                           frequency(x.ts)), method = "CSS")
        fit.aic <- -2 * fit$loglik + (log(n) + 1) * length(fit$coef)
        print(paste(paste(c(p,d,q,P,D,Q), collapse = "-"), "AIC:", fit.aic))
        if (fit.aic < best.aic)
        {
          best.aic <- fit.aic
          best.fit <- fit
          best.model <- c(p,d,q,P,D,Q)
        }
      }
   list(best.aic, best.fit, best.model)
 }

best.arima.elec <- get.best.arima(
  log(Elec.ts),
  maxord = c(2,2,2,2,2,2))

best.fit.elec <- best.arima.elec[[2]]
acf(resid(best.fit.elec))
best.arima.elec[[3]]
ts.plot(cbind(window(Elec.ts,start = 1981),
  exp(predict(best.fit.elec,12)$pred) ), lty = 1:2)
Show the Tidyverts code in full 
elec_ts |>
  model(
    ar_model = ARIMA(log(elec) ~ 1 +
      pdq(1, 1, 0) +
      PDQ(1, 0, 0)),
    ma_model = ARIMA(log(elec) ~ 1 + 
      pdq(0, 1, 1) +
      PDQ(0, 0, 1))) |>
  glance() |> 
  pull(AIC)

best_fit_elec <- elec_ts |>
  model(
    ar_model = ARIMA(log(elec) ~ 1 +
      pdq(0:2, 0:2, 0:2) +
      PDQ(0:2, 0:2, 0:2), approximation = TRUE))

best_fit_elec |>
  residuals() |>
  ACF() |>
  autoplot()

glance(best_fit_elec) |> pull(AIC)

best_fit_elec |>
  forecast(h = "12 months") |>
  autoplot(filter(elec_ts, date > ymd("1981-01-01")))



# Very Slow, but you can see all fits.
# get_arima <- function(p, d, q, P, D, Q, data = elec_ts) {
#   model(data, arima = ARIMA(log(elec) ~ 1 +
#       pdq(p, d, q) + PDQ(P, D, Q), approximation = TRUE))
# }
# get_aic <- function(fit) {
#   gfit <- glance(fit)
#   if (nrow(gfit) != 0) {
#     pull(gfit, AIC)  
#   } else {
#     NA
#   }
#    }


# all_possible <- expand_grid(
#   p = 0:2, d = 0:2, q = 0:2,
#   P = 0:2, D = 0:2, Q = 0:2)

# all_possible <- all_possible |>
#   mutate(
#     fit = purrr::pmap(all_possible, get_arima),
#     aic = purrr::map_dbl(fit, ~get_aic(.x))
#     )

# filter(all_possible, aic == min(aic, na.rm = TRUE))

7.4.1 “S&P500 Series” Modern Look

Book code

library(MASS)
data(SP500)
plot(SP500, type = 'l')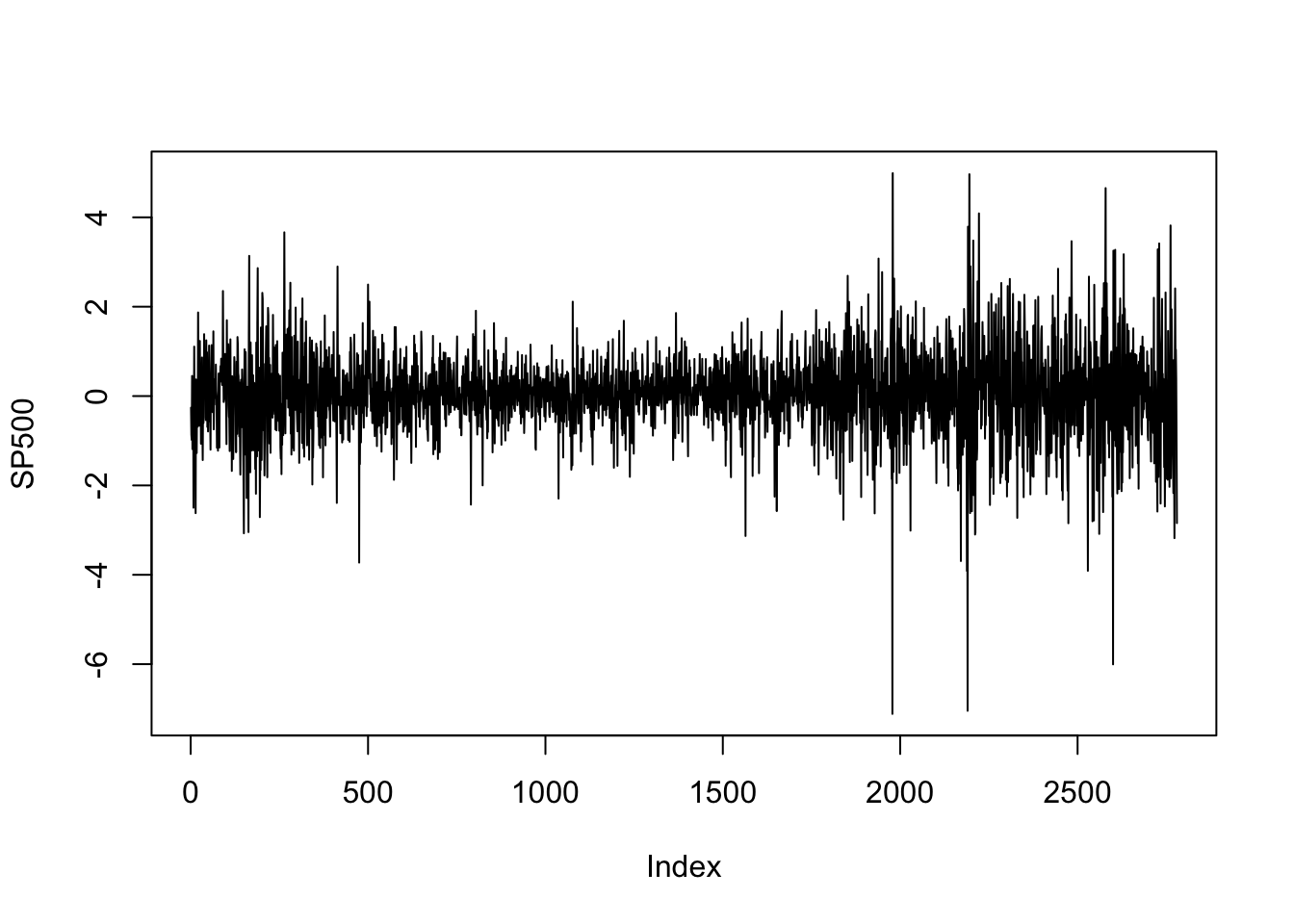

Tidyverts code

library(MASS)
data(SP500)
dat <- tibble(x = SP500) |>
  mutate(
    sq_mean_diff = (x - mean(x))^2,
    index = 1:n()) |>
  as_tsibble(index = index)
autoplot(dat)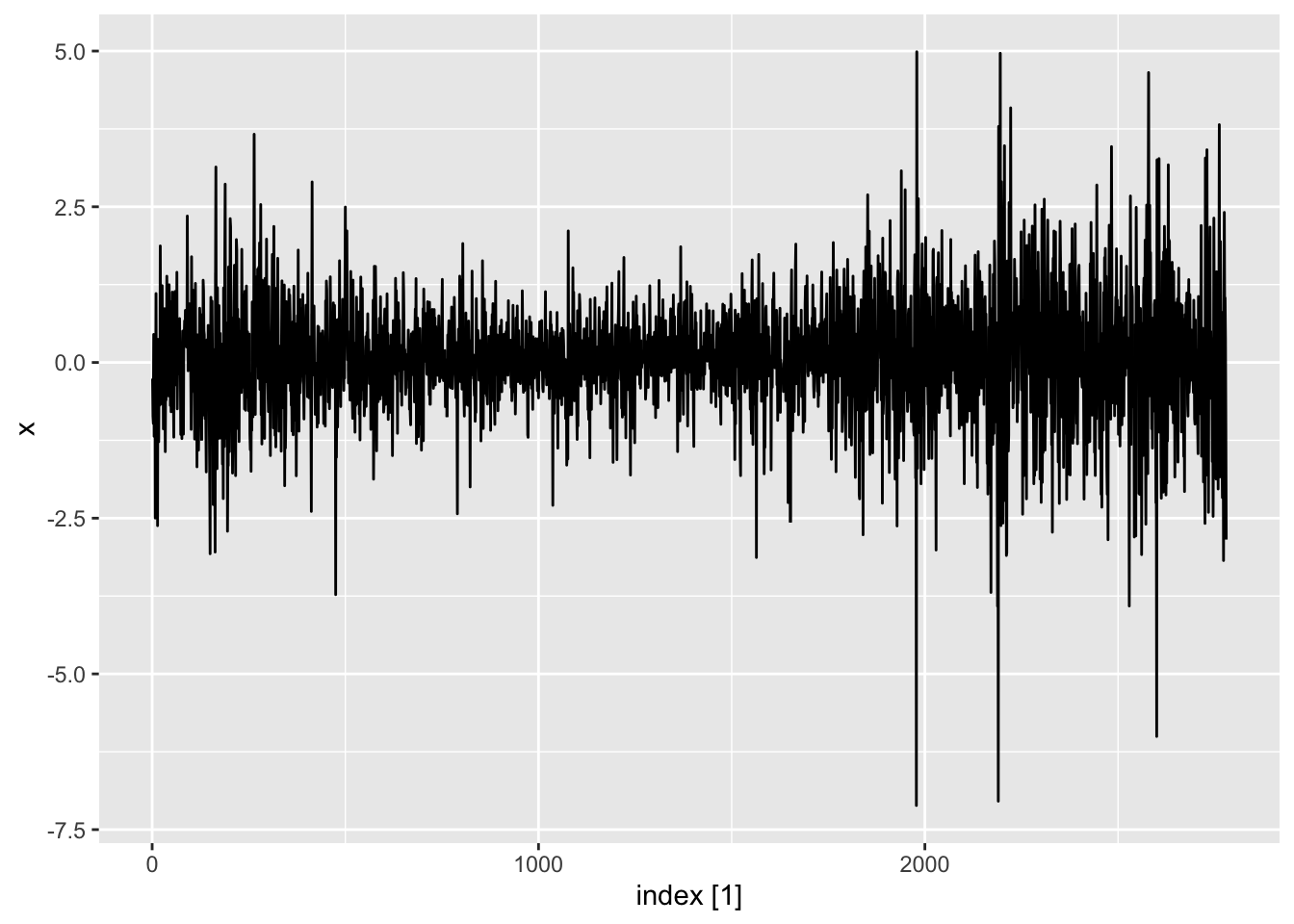

acf(SP500)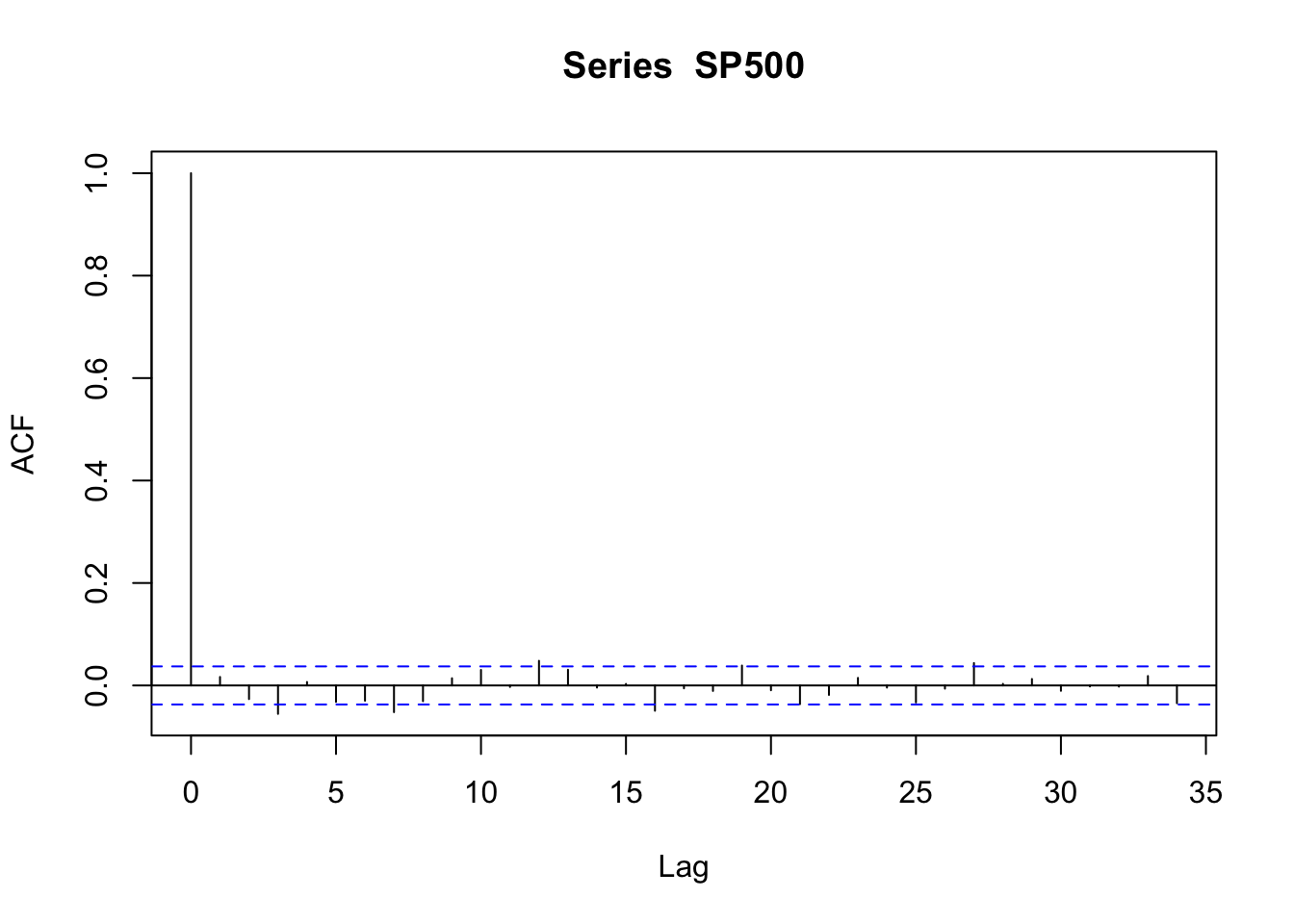

ACF(dat) |> autoplot()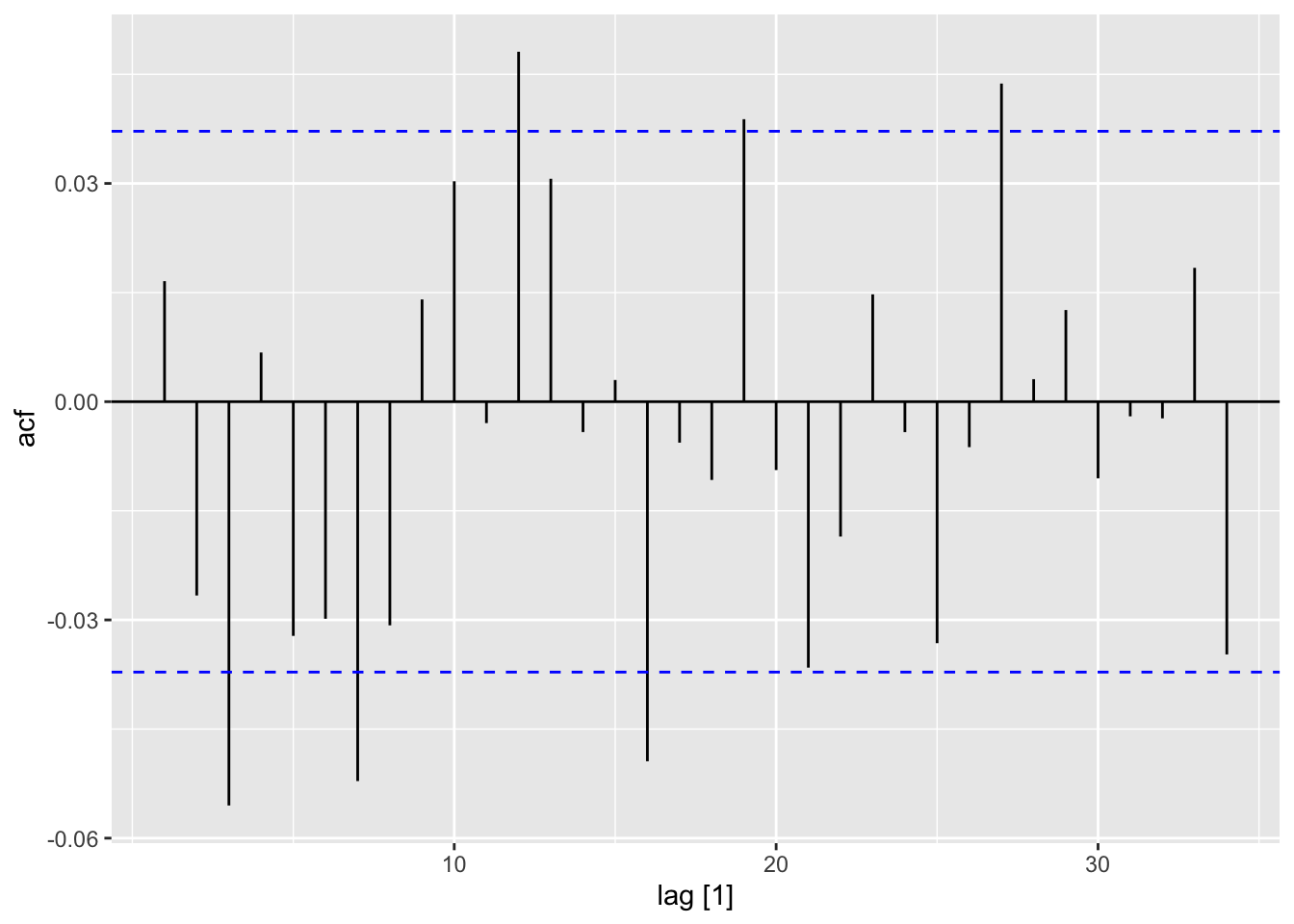

acf((SP500 - mean(SP500))^2)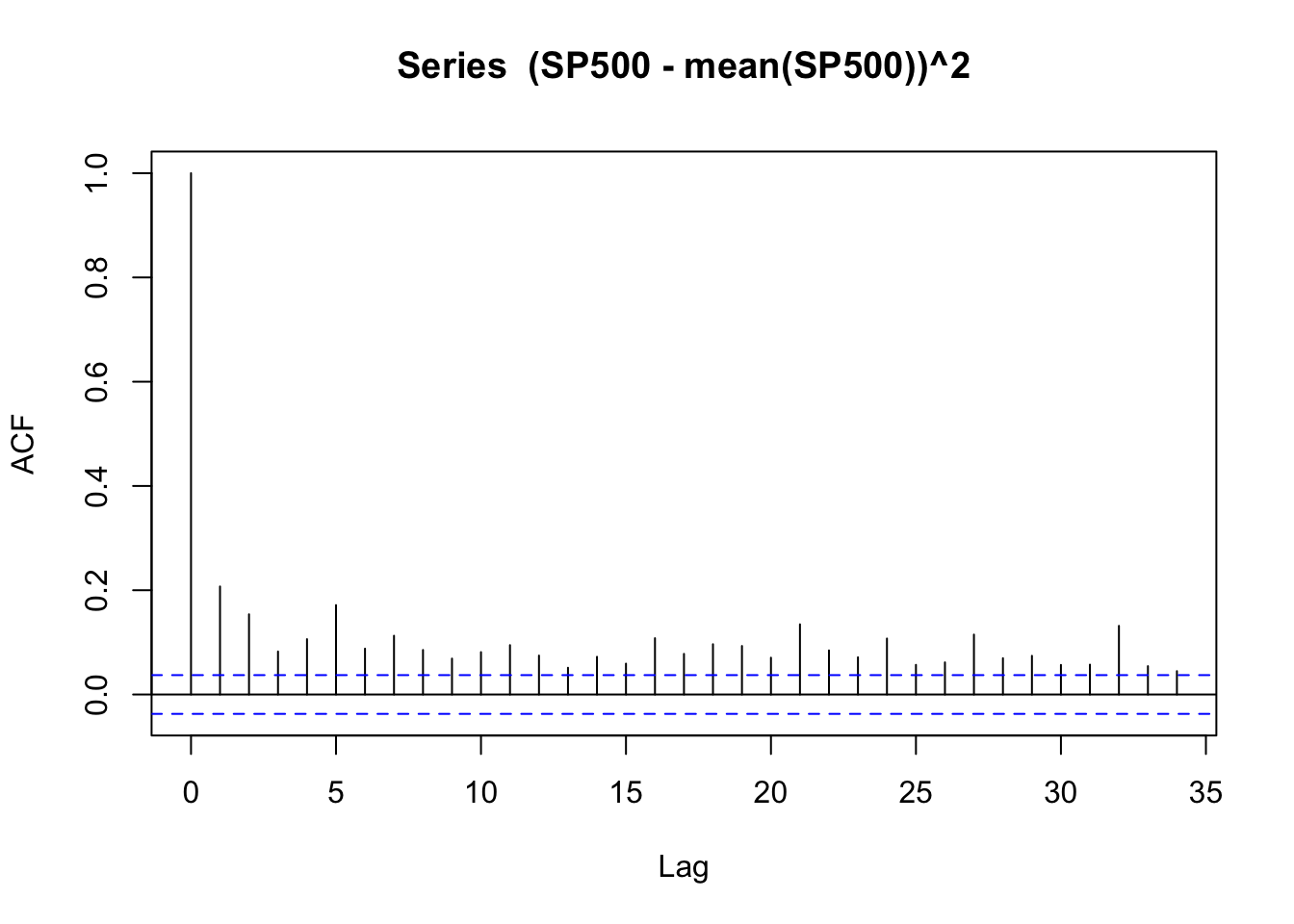

ACF(dat, y = sq_mean_diff) |> autoplot()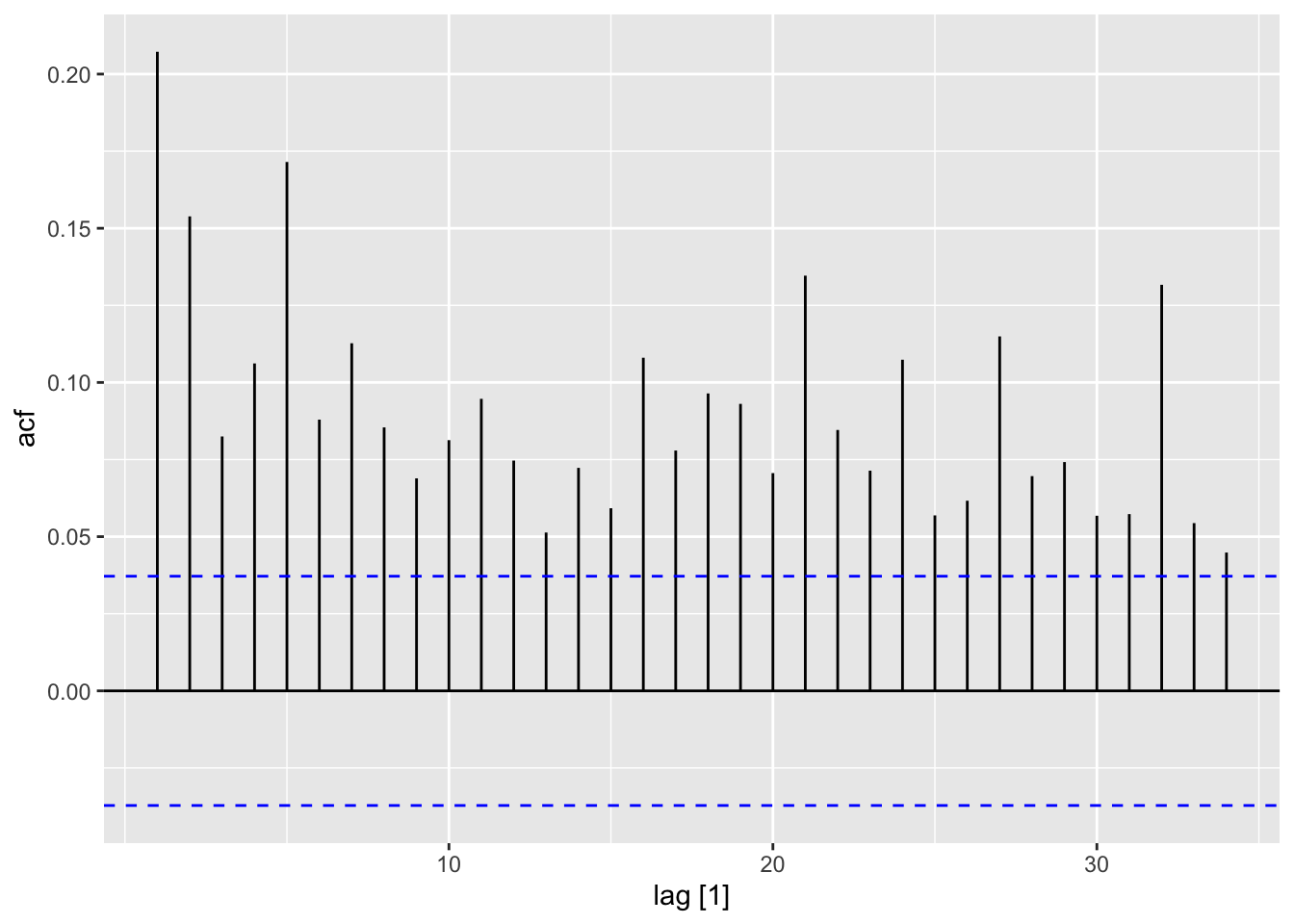

Show the Book code in full 
library(MASS)
data(SP500)
plot(SP500, type = 'l')
acf(SP500)
acf((SP500 - mean(SP500))^2)
Show the Tidyverts code in full 
library(MASS)
data(SP500)
dat <- tibble(x = SP500) |>
  mutate(
    sq_mean_diff = (x - mean(x))^2,
    index = 1:n()) |>
  as_tsibble(index = index)
autoplot(dat)
ACF(dat) |> autoplot()
ACF(dat, y = sq_mean_diff) |> autoplot()

7.4.4 “Simulation and fitted GARCH model” Modern Look

Book code

library(tseries)
set.seed(1)
alpha0 <- 0.1
alpha1 <- 0.4
beta1 <- 0.2
w <- rnorm(10000)
a <- rep(0, 10000)
h <- rep(0, 10000)
for (i in 2:10000) {
  h[i] <- alpha0 + alpha1 * (a[i - 1]^2) + beta1 * h[i - 1]
  a[i] <- w[i] * sqrt(h[i])
  }
acf(a)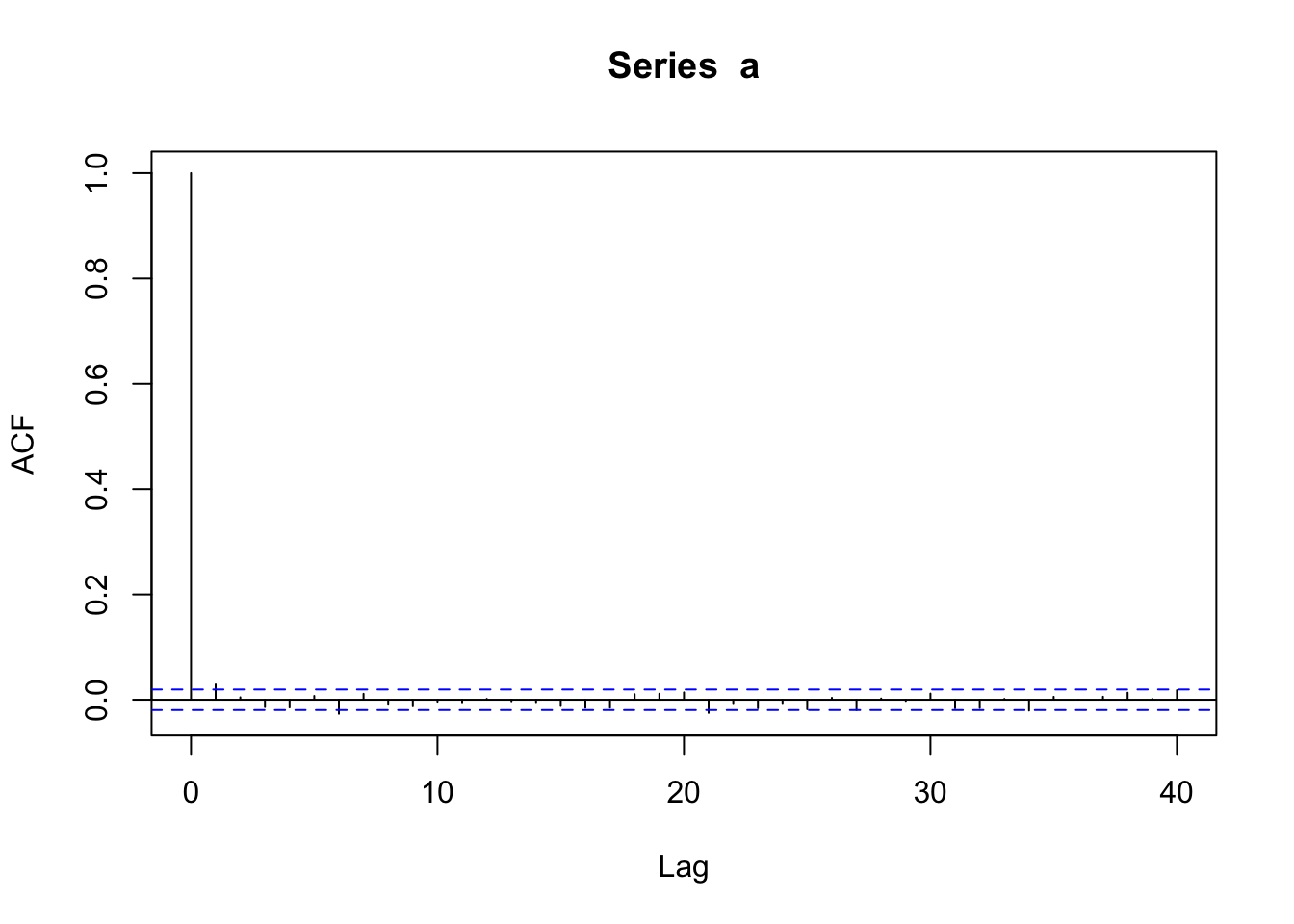

Tidyverts code

pacman::p_load("rugarch")
set.seed(1)
sim <- tibble(
  alpha0 = 0.1,
  alpha1 = 0.4,
  beta1 = 0.2,
  w = rnorm(10000),
  a = rep(0, 10000),
  h = rep(0, 10000)) |>
  mutate(index = 1:n()) |>
  as_tsibble(index = index)

for (i in 2:10000) {
  sim$h[i] <- sim$alpha0[1] + sim$alpha1[1] * (sim$a[i - 1]^2) + sim$beta1[1] * sim$h[i - 1]
  sim$a[i] <- sim$w[i] * sqrt(sim$h[i])
  }
sim <- mutate(sim, a2 = a^2)

ACF(sim, y = a) |>
  autoplot()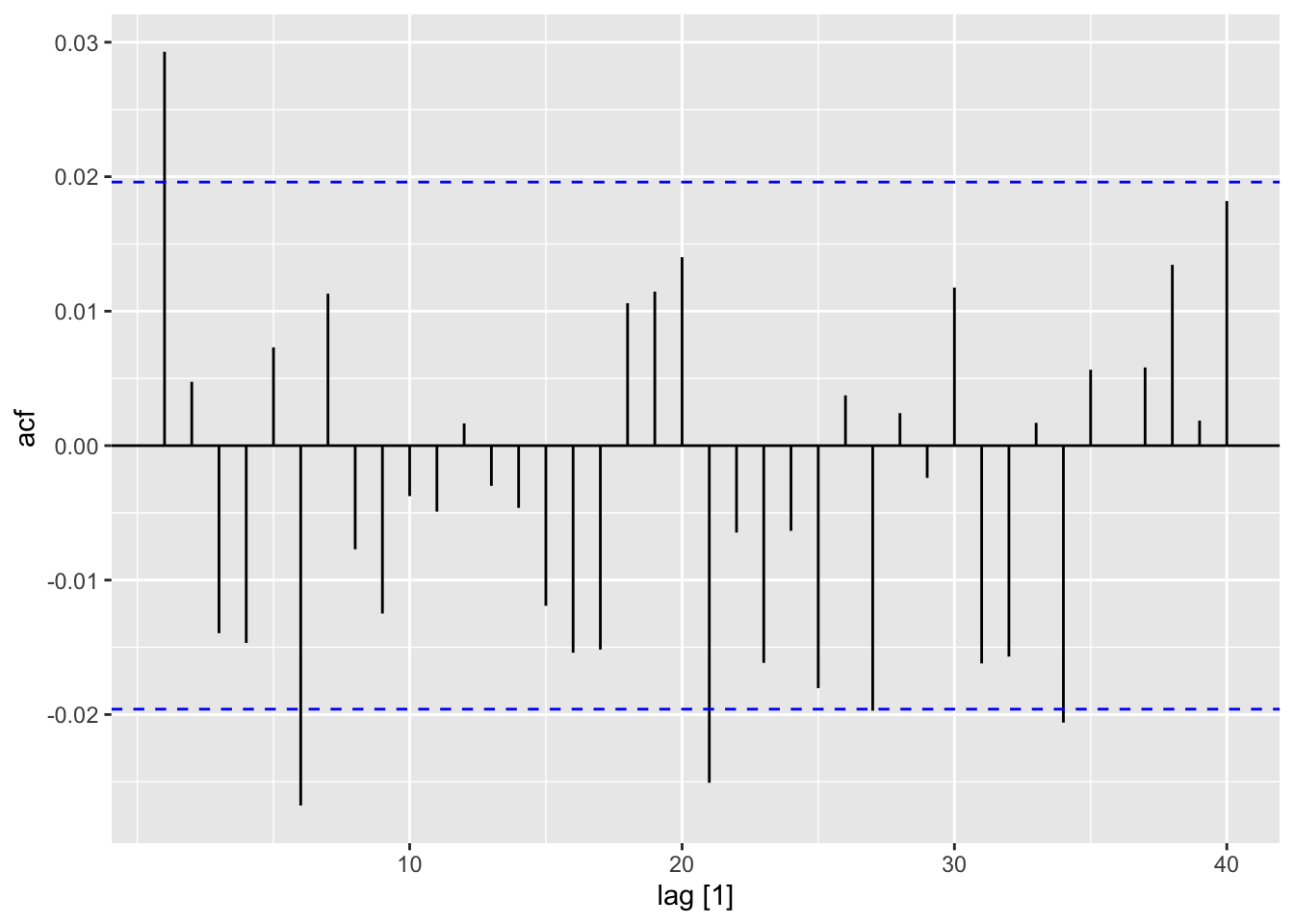

acf(a^2)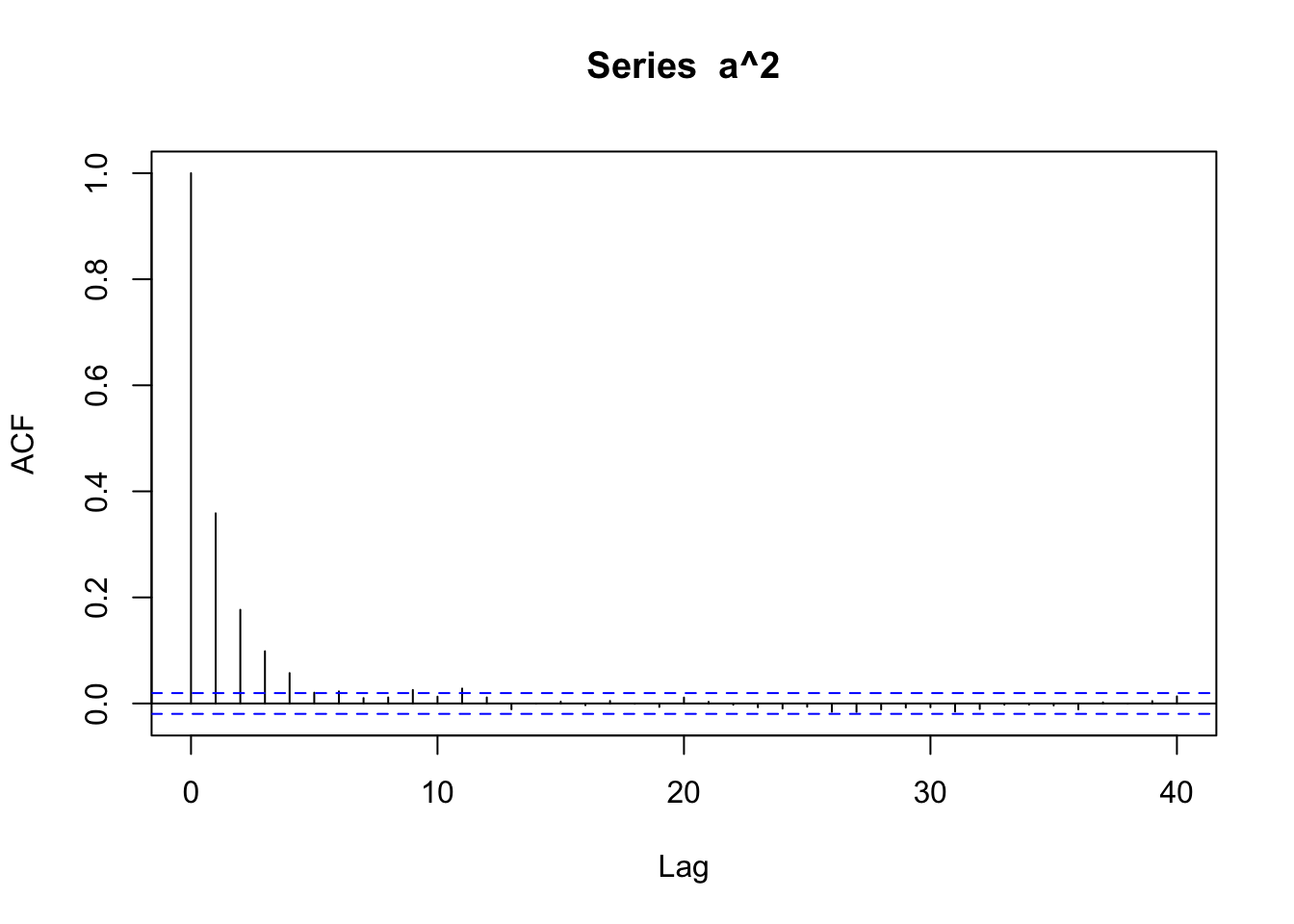

ACF(sim, y = a2) |>
  autoplot()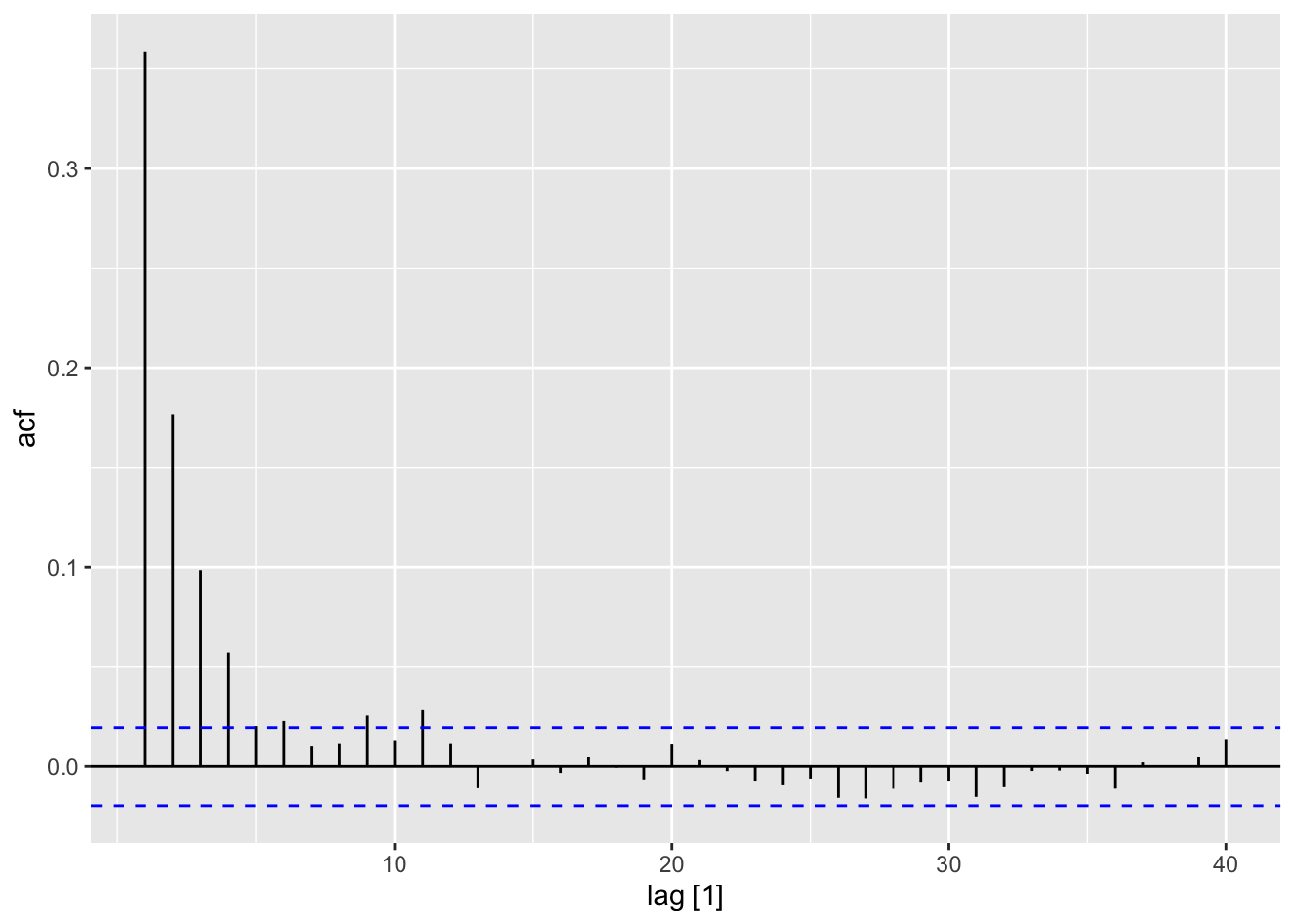

a.garch <- garch(a, grad = "numerical", trace = FALSE)
confint(a.garch)
       2.5 %    97.5 %
a0 0.0882393 0.1092903
a1 0.3307897 0.4023932
b1 0.1928344 0.2954660
spec <- ugarchspec(
    mean.model = list(armaOrder = c(0,0)),
    variance.model = list(model = "sGARCH"),
    distribution.model = "norm")

sim_garch <- ugarchfit(data = pull(sim,a), spec = spec)

confint(sim_garch)
              2.5 %      97.5 %
mu     -0.008260573 0.008253128
omega   0.088325823 0.109204574
alpha1  0.331527684 0.401653876
beta1   0.192934674 0.295362333
Show the Book code in full 
library(tseries)
set.seed(1)
alpha0 <- 0.1
alpha1 <- 0.4
beta1 <- 0.2
w <- rnorm(10000)
a <- rep(0, 10000)
h <- rep(0, 10000)
for (i in 2:10000) {
  h[i] <- alpha0 + alpha1 * (a[i - 1]^2) + beta1 * h[i - 1]
  a[i] <- w[i] * sqrt(h[i])
  }
acf(a)
acf(a^2)

a.garch <- garch(a, grad = "numerical", trace = FALSE)
confint(a.garch)
Show the Tidyverts code in full 
pacman::p_load("rugarch")
set.seed(1)
sim <- tibble(
  alpha0 = 0.1,
  alpha1 = 0.4,
  beta1 = 0.2,
  w = rnorm(10000),
  a = rep(0, 10000),
  h = rep(0, 10000)) |>
  mutate(index = 1:n()) |>
  as_tsibble(index = index)

for (i in 2:10000) {
  sim$h[i] <- sim$alpha0[1] + sim$alpha1[1] * (sim$a[i - 1]^2) + sim$beta1[1] * sim$h[i - 1]
  sim$a[i] <- sim$w[i] * sqrt(sim$h[i])
  }
sim <- mutate(sim, a2 = a^2)

ACF(sim, y = a) |>
  autoplot()
ACF(sim, y = a2) |>
  autoplot()

spec <- rurgarch::ugarchspec(
    mean.model = list(armaOrder = c(0,0)),
    variance.model = list(model = "sGARCH"),
    distribution.model = "norm")

sim_garch <- ugarchfit(data = pull(sim,a), spec = spec)

confint(sim_garch)
# gd <- ugarchdistribution(garchfit, n.sim = 500, recursive = TRUE,
#  recursive.length = 6000, recursive.window = 500, m.sim = 100,
#  solver = 'hybrid')
#garchforecast <- ugarchforecast(fitORspec = garchfit, n.ahead = 5)

7.4.5 “Fit to S&P500 series” Modern Look

Book code

sp.garch <- garch(SP500, trace = F)
sp.res   <- sp.garch$res[-1]
acf(sp.res)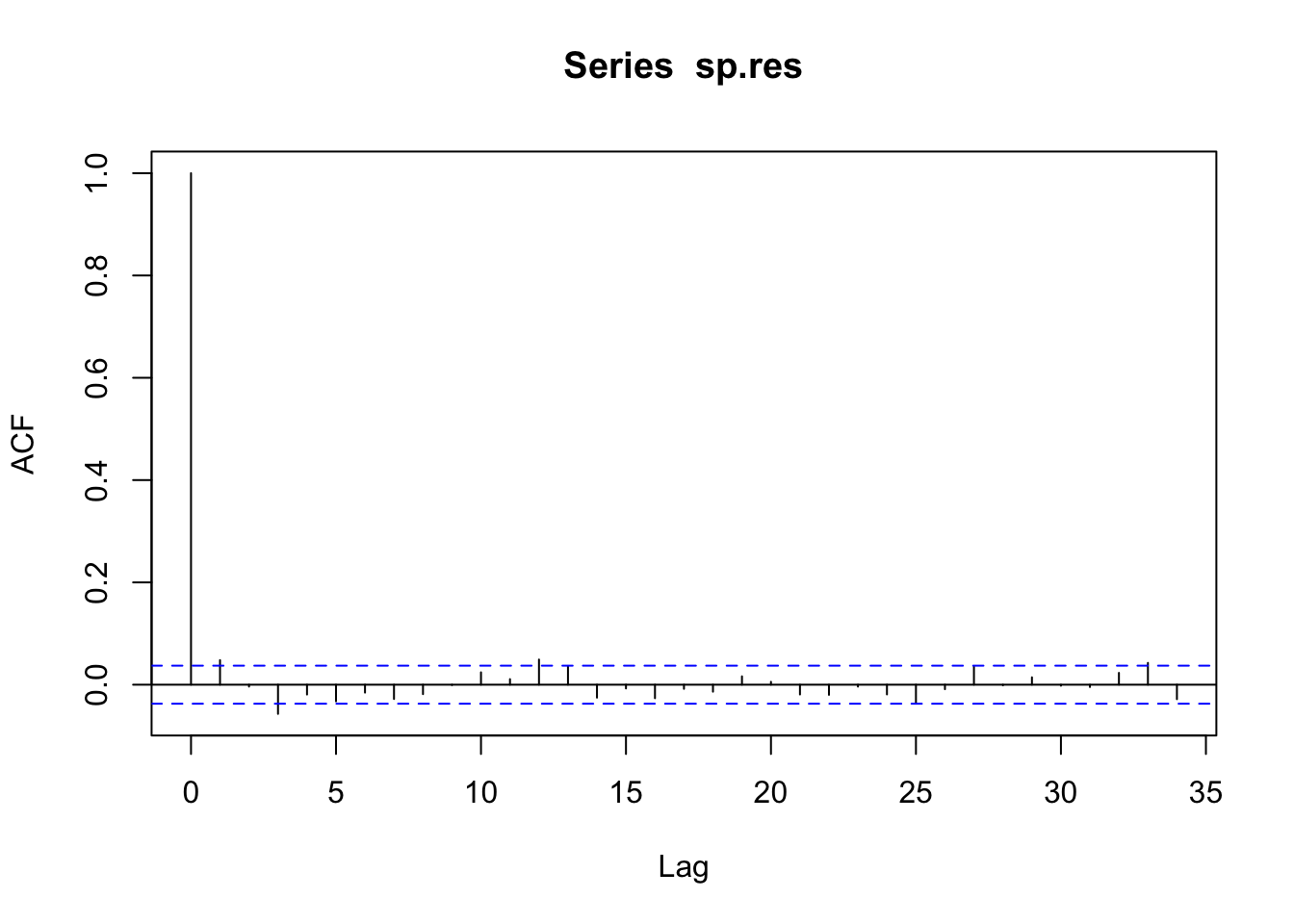

Tidyverts code

dat <- tibble::tibble(sp500 = SP500) |>
  mutate(index = 1:n()) |>
  as_tsibble(index = index)

spec <- ugarchspec(
    mean.model = list(armaOrder = c(0,0)),
    variance.model = list(model = "sGARCH"),
    distribution.model = "norm")

sp_garch <- ugarchfit(data = pull(dat, sp500), spec = spec)

dat <- dat |>
  mutate(
    .resid = residuals(sp_garch),
    .resid2 = .resid^2)

dat |>
  ACF(y = .resid) |>
  autoplot()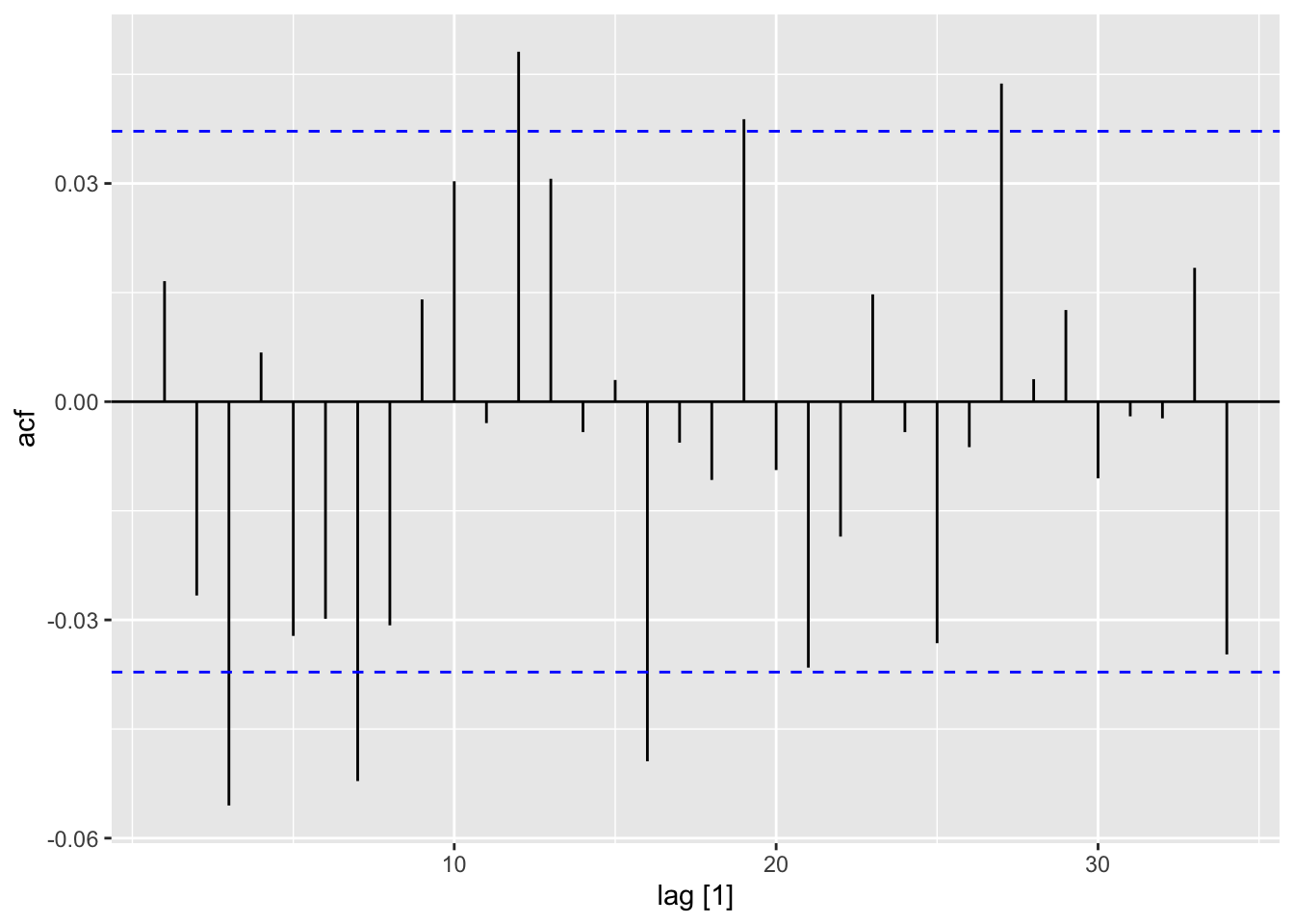

acf(sp.res^2)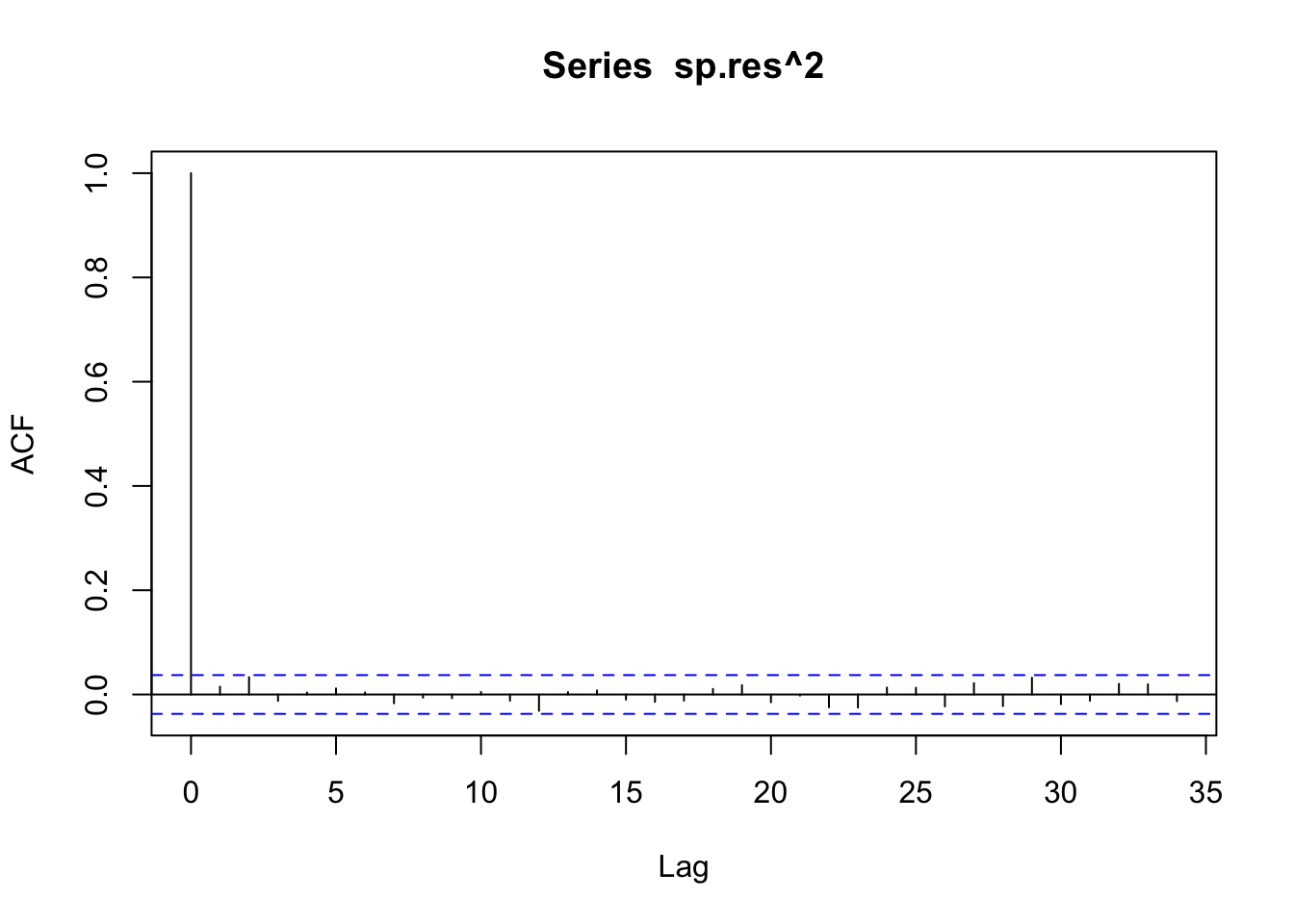

dat |>
  ACF(y = .resid2) |>
  autoplot()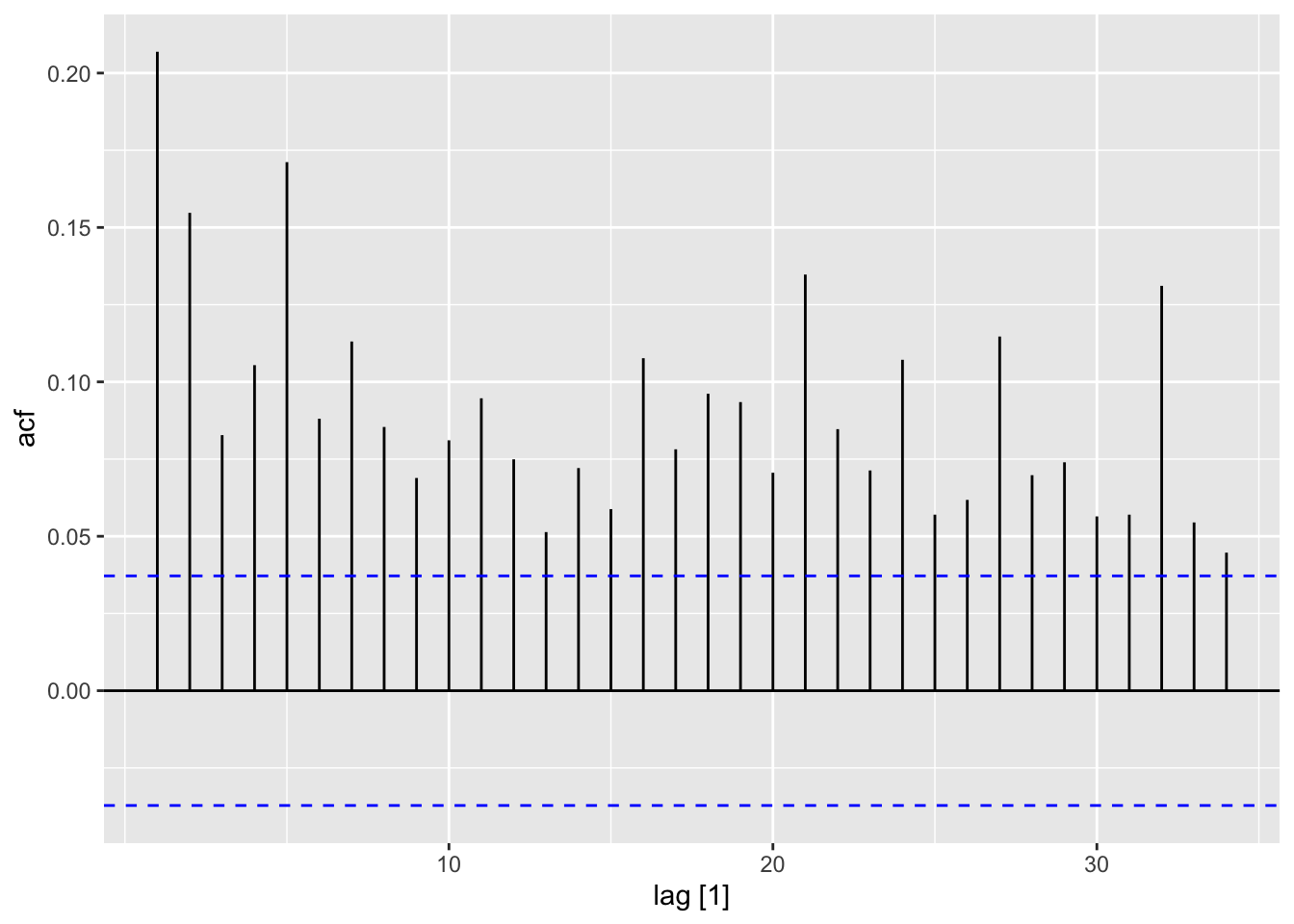

Show the Book code in full 
sp.garch <- garch(SP500, trace = F)
sp.res   <- sp.garch$res[-1]
acf(sp.res)
acf(sp.res^2)
Show the Tidyverts code in full 
dat <- tibble::tibble(sp500 = SP500) |>
  mutate(index = 1:n()) |>
  as_tsibble(index = index)

spec <- ugarchspec(
    mean.model = list(armaOrder = c(0,0)),
    variance.model = list(model = "sGARCH"),
    distribution.model = "norm")

sp_garch <- ugarchfit(data = pull(dat, sp500), spec = spec)

dat <- dat |>
  mutate(
    .resid = residuals(sp_garch),
    .resid2 = .resid^2)

dat |>
  ACF(y = .resid) |>
  autoplot()

dat |>
  ACF(y = .resid2) |>
  autoplot()

7.4.6 “Volatility in climate series” Modern Look

Book code

stemp <- scan("data/stemp.dat")
stemp.ts <- ts(stemp, start = 1850, freq = 12)
plot(stemp.ts)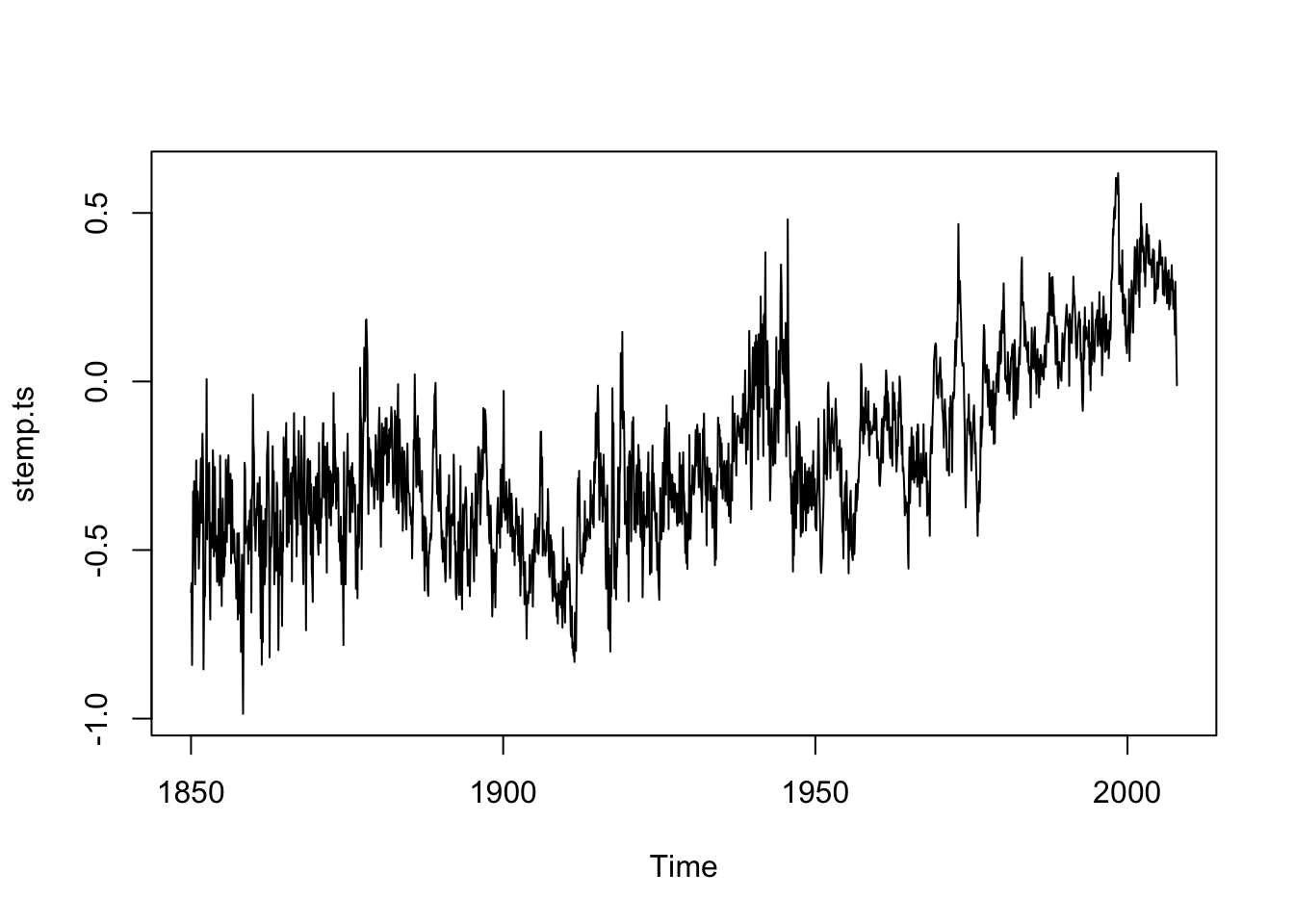

stemp.best <- get.best.arima(stemp.ts, maxord = rep(2,6))
stemp.best[[3]]
[1] 1 1 2 2 0 1
stemp.arima <- arima(stemp.ts, order = c(1,1,2),
  seas = list(order = c(2,0,1), 12))
t(confint(stemp.arima))
             ar1       ma1       ma2      sar1        sar2       sma1
2.5 %  0.8317390 -1.447400 0.3256700 0.8576802 -0.02501883 -0.9690534
97.5 % 0.9127946 -1.312553 0.4530475 1.0041396  0.07413424 -0.8507034

Tidyverts code

stemp_ts <- tibble::tibble(stemp = scan("data/stemp.dat")) |>
  mutate(
    date = seq(
      ymd("1850-01-01"),
      by = "1 months",
      length.out = n()),
      year_month = tsibble::yearmonth(date)) |>
  as_tsibble(index = year_month)
autoplot(stemp_ts)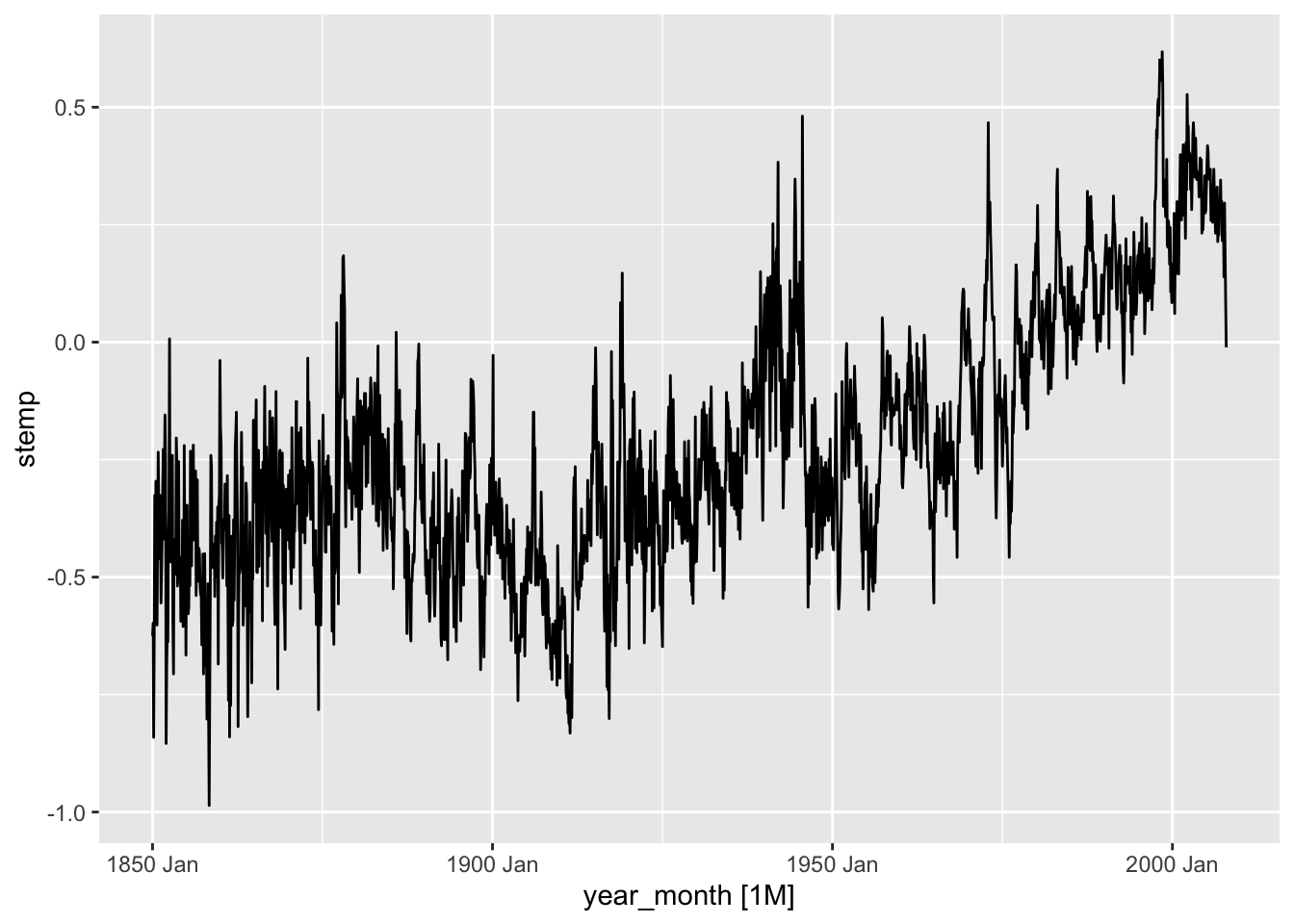

stemp_best <- stemp_ts |>
  model(
    ar_model = ARIMA(stemp ~ 1 +
      pdq(0:2, 0:2, 0:2) +
      PDQ(0:2, 0:2, 0:2), approximation = TRUE),
    book_arima = ARIMA(stemp ~ 1 + 
      pdq(1, 1, 2) +
      PDQ(2, 0, 1), approximation = TRUE),
    book_arima_reduced = ARIMA(stemp ~ 1 + 
      pdq(1, 1, 2) +
      PDQ(1, 0, 1), approximation = TRUE),
      )

tidy(stemp_best) |>
  dplyr::filter(term != "constant") |>
  mutate(
    lb = round(estimate + qnorm(.025) * std.error, 3),
    ub = round(estimate + qnorm(.975) * std.error, 3),
    interval = paste0(lb, " , ", ub)
  ) |>
  dplyr::select(.model, term, interval) |>
  pivot_wider(names_from = .model, values_from = interval, values_fill = "-") |>
  knitr::kable()
term ar_model book_arima book_arima_reduced
ar1 0.449 , 0.546 0.838 , 0.917 0.835 , 0.913
ar2 0.161 , 0.257 - -
ma1 -0.99 , -0.954 -1.452 , -1.319 -1.45 , -1.317
sar1 -0.01 , 0.083 0.845 , 0.997 0.917 , 0.995
sar2 -0.028 , 0.065 -0.023 , 0.077 -
ma2 - 0.33 , 0.456 0.328 , 0.454
sma1 - -0.964 , -0.837 -0.968 , -0.859 
stemp.arima <- arima(stemp.ts, order = c(1,1,2),
  seas = list(order = c(1,0,1), 12))
t(confint(stemp.arima))
             ar1       ma1       ma2      sar1       sma1
2.5 %  0.8303969 -1.445048 0.3242572 0.9243526 -0.9694910
97.5 % 0.9108148 -1.311229 0.4508903 0.9956640 -0.8679276
tidy(stemp_best) |>
  dplyr::filter(term != "constant") |>
  mutate(
    lb = round(estimate + qnorm(.025) * std.error, 3),
    ub = round(estimate + qnorm(.975) * std.error, 3),
    interval = paste0(lb, " , ", ub)
  ) |>
  dplyr::select(.model, term, interval) |>
  pivot_wider(names_from = .model, values_from = interval, values_fill = "-") |>
  knitr::kable()
term ar_model book_arima book_arima_reduced
ar1 0.449 , 0.546 0.838 , 0.917 0.835 , 0.913
ar2 0.161 , 0.257 - -
ma1 -0.99 , -0.954 -1.452 , -1.319 -1.45 , -1.317
sar1 -0.01 , 0.083 0.845 , 0.997 0.917 , 0.995
sar2 -0.028 , 0.065 -0.023 , 0.077 -
ma2 - 0.33 , 0.456 0.328 , 0.454
sma1 - -0.964 , -0.837 -0.968 , -0.859 
stemp.res <- resid(stemp.arima)
layout(1:2)
acf(stemp.res)
acf(stemp.res^2)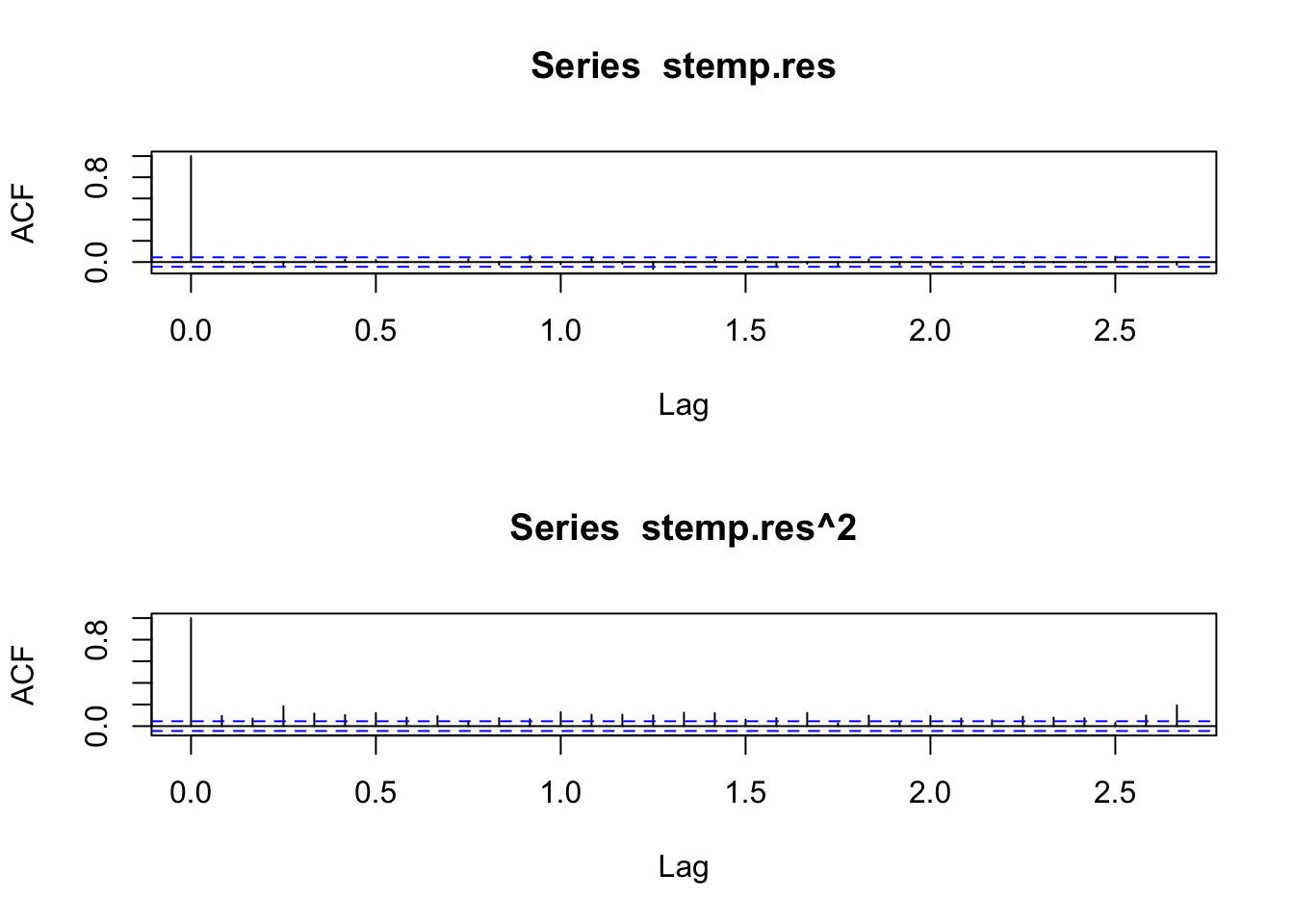

stemp_res <- stemp_best |>
  dplyr::select(book_arima_reduced) |>
  residuals() |>
  mutate(.resid2 = .resid^2)

rp <- ACF(stemp_res, y = .resid) |> autoplot()
r2p <- ACF(stemp_res, y = .resid2) |> autoplot()
rp / r2p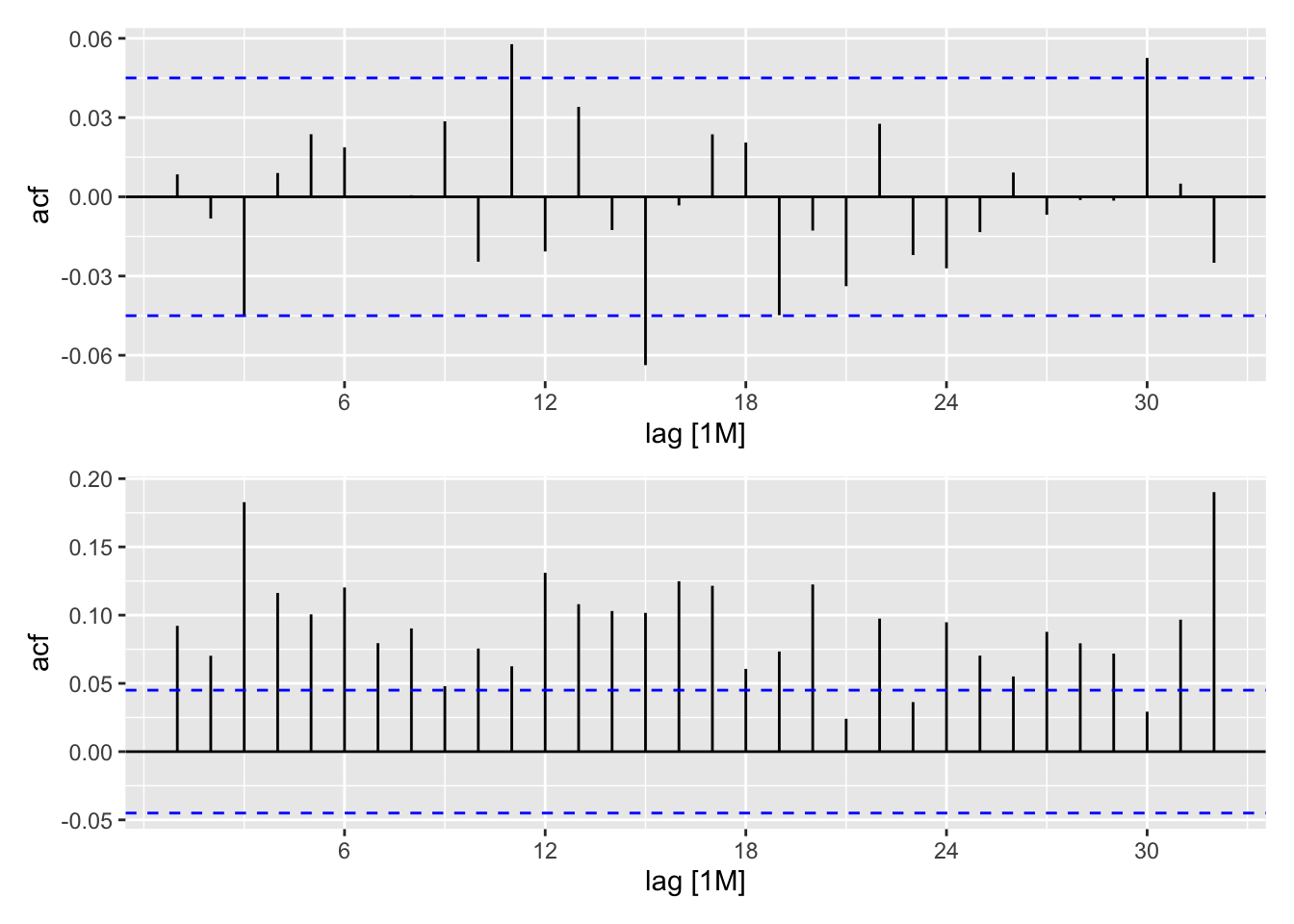

stemp.garch <- garch(stemp.res, trace = F)
confint(stemp.garch)
          2.5 %       97.5 %
a0 1.064246e-05 0.0001485812
a1 3.299179e-02 0.0652567733
b1 9.249316e-01 0.9630787389
spec <- ugarchspec(
    mean.model = list(armaOrder = c(0,0)),
    variance.model = list(model = "sGARCH"),
    distribution.model = "norm")

stemp_garch <- ugarchfit(data = pull(stemp_res, .resid), spec = spec)
confint(stemp_garch)
               2.5 %       97.5 %
mu     -3.974225e-03 0.0044798310
omega   2.246930e-06 0.0001533503
alpha1  2.884755e-02 0.0691398769
beta1   9.215237e-01 0.9670927847
stemp.garch.res <- resid(stemp.garch)[-1]
layout(1:2)
acf(stemp.garch.res)
acf(stemp.garch.res^2)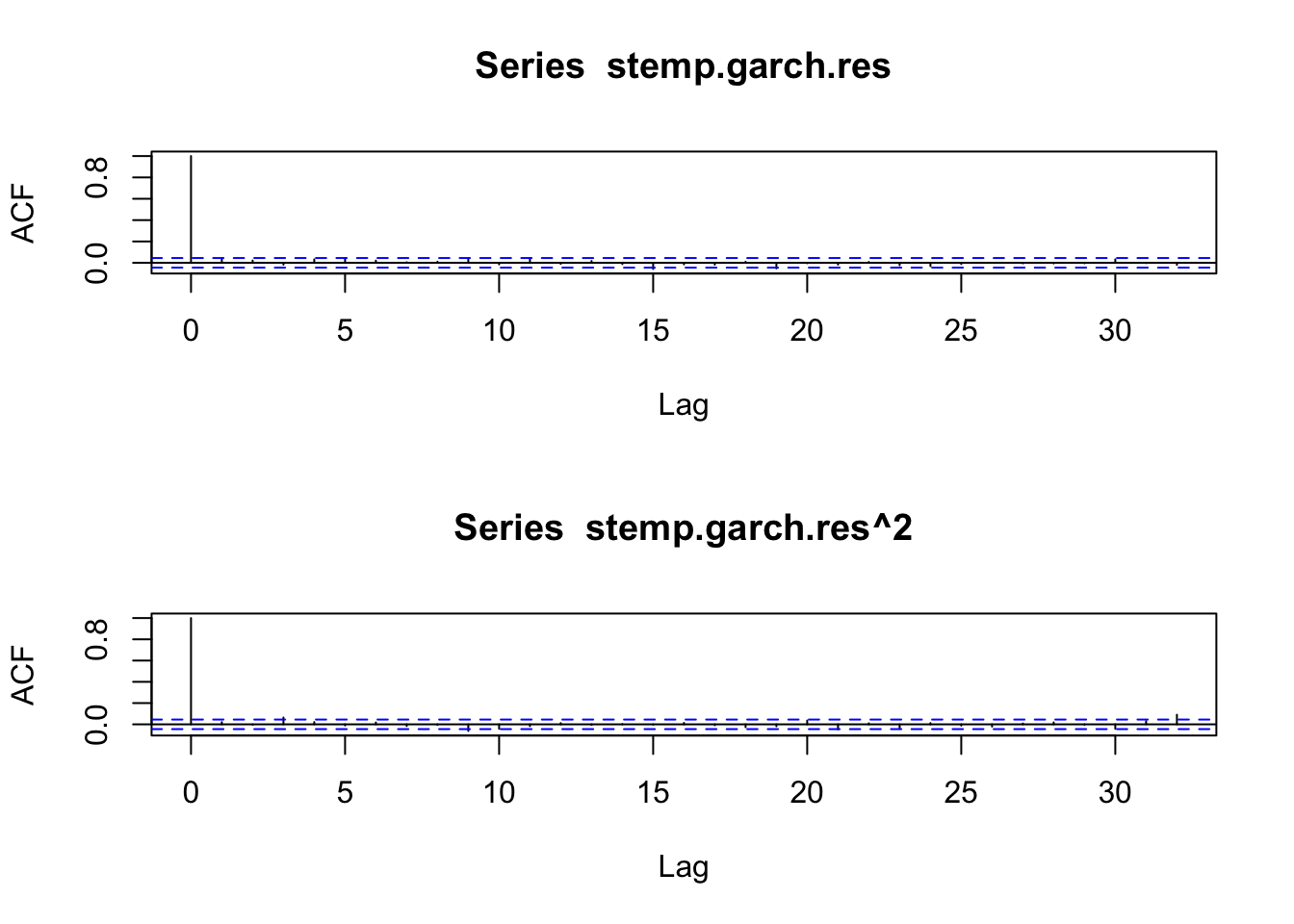

stemp_res <- stemp_res |>
  mutate(
    .resid_garch = residuals(stemp_garch),
    .resid2_garch = .resid_garch^2)

rgp <- ACF(stemp_res, y = .resid_garch) |> autoplot()
rg2p <- ACF(stemp_res, y = .resid2_garch) |> autoplot()
rgp / rg2p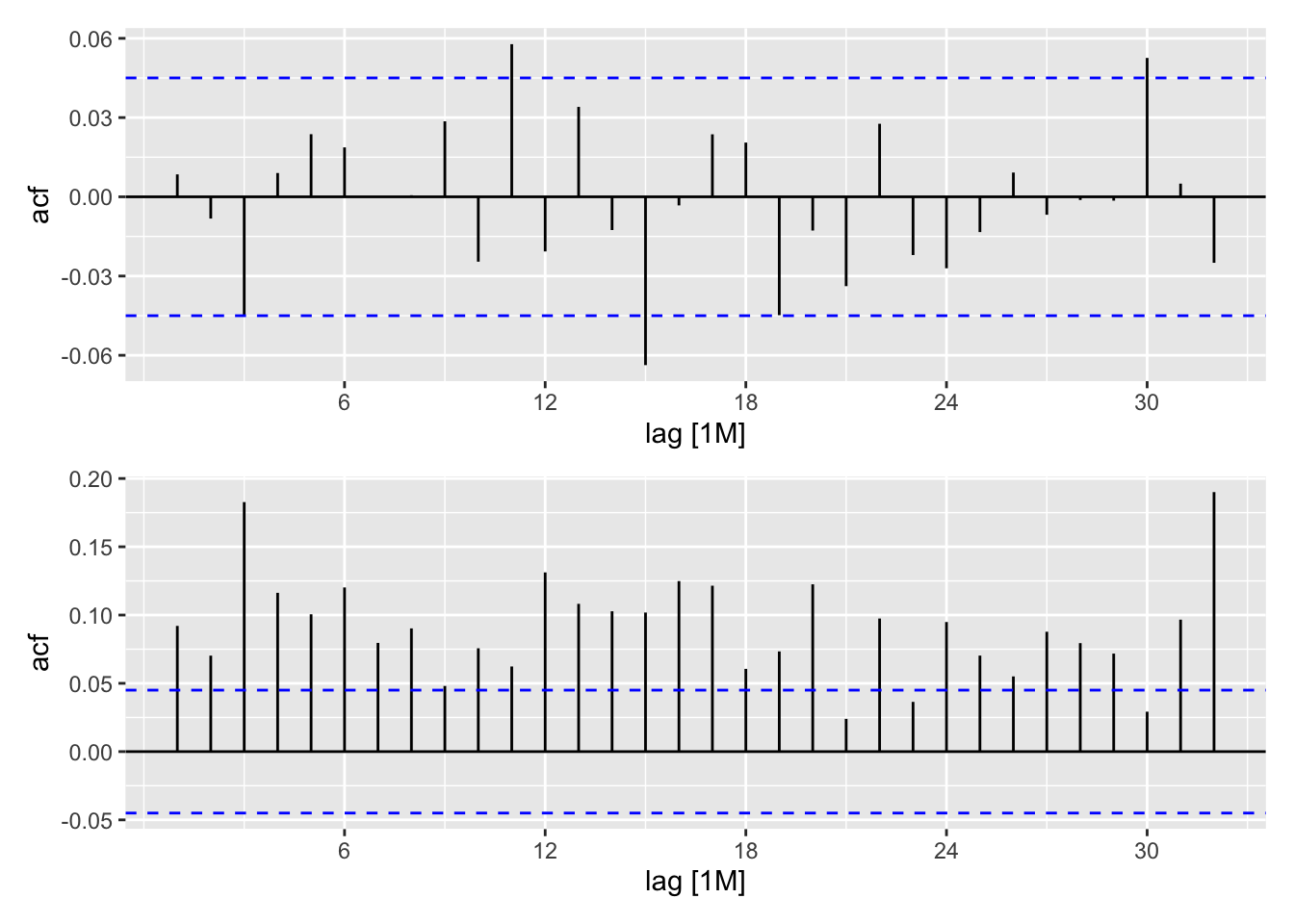

Show the Book code in full 
stemp <- scan("data/stemp.dat")
stemp.ts <- ts(stemp, start = 1850, freq = 12)
plot(stemp.ts)
stemp.best <- get.best.arima(stemp.ts, maxord = rep(2,6))
stemp.best[[3]]
stemp.arima <- arima(stemp.ts, order = c(1,1,2),
  seas = list(order = c(2,0,1), 12))
t(confint(stemp.arima))

stemp.arima <- arima(stemp.ts, order = c(1,1,2),
  seas = list(order = c(1,0,1), 12))
t(confint(stemp.arima))
stemp.res <- resid(stemp.arima)
layout(1:2)
acf(stemp.res)
acf(stemp.res^2)
stemp.garch <- garch(stemp.res, trace = F)
confint(stemp.garch)
stemp.garch.res <- resid(stemp.garch)[-1]
acf(stemp.garch.res)
acf(stemp.garch.res^2)
Show the Tidyverts code in full 
stemp_ts <- tibble::tibble(stemp = scan("data/stemp.dat")) |>
  mutate(
    date = seq(
      ymd("1850-01-01"),
      by = "1 months",
      length.out = n()),
      year_month = tsibble::yearmonth(date)) |>
  as_tsibble(index = year_month)
autoplot(stemp_ts)

stemp_best <- stemp_ts |>
  model(
    ar_model = ARIMA(stemp ~ 1 +
      pdq(0:2, 0:2, 0:2) +
      PDQ(0:2, 0:2, 0:2), approximation = TRUE),
    book_arima = ARIMA(stemp ~ 1 + 
      pdq(1, 1, 2) +
      PDQ(2, 0, 1), approximation = TRUE),
    book_arima_reduced = ARIMA(stemp ~ 1 + 
      pdq(1, 1, 2) +
      PDQ(1, 0, 1), approximation = TRUE),
      )

tidy(stemp_best) |>
  dplyr::filter(term != "constant") |>
  mutate(
    lb = round(estimate + qnorm(.025) * std.error, 3),
    ub = round(estimate + qnorm(.975) * std.error, 3),
    interval = paste0(lb, " , ", ub)
  ) |>
  dplyr::select(.model, term, interval) |>
  pivot_wider(names_from = .model, values_from = interval, values_fill = "-") |>
  knitr::kable()
  
stemp_res <- stemp_best |>
  dplyr::select(book_fit_reduced) |>
  residuals() |>
  mutate(.resid2 = .resid^2)

rp <- ACF(stemp_res, y = .resid) |> autoplot()
r2p <- ACF(stemp_res, y = .resid2) |> autoplot()
rp / r2p



spec <- ugarchspec(
    mean.model = list(armaOrder = c(0,0)),
    variance.model = list(model = "sGARCH"),
    distribution.model = "norm")

stemp_garch <- ugarchfit(data = pull(stemp_res, .resid), spec = spec)
confint(stemp_garch)

stemp.garch <- garch(stemp.res, trace = F)
t(confint(stemp.garch)

stemp_res <- stemp_res |>
  mutate(
    .resid_garch = residuals(stemp_garch),
    .resid2_garch = .resid_garch^2)

rgp <- ACF(stemp_res, y = .resid_garch) |> autoplot()
rg2p <- ACF(stemp_res, y = .resid2_garch) |> autoplot()
rgp / rg2p

7.5 Summary of Modern R commands used in examples