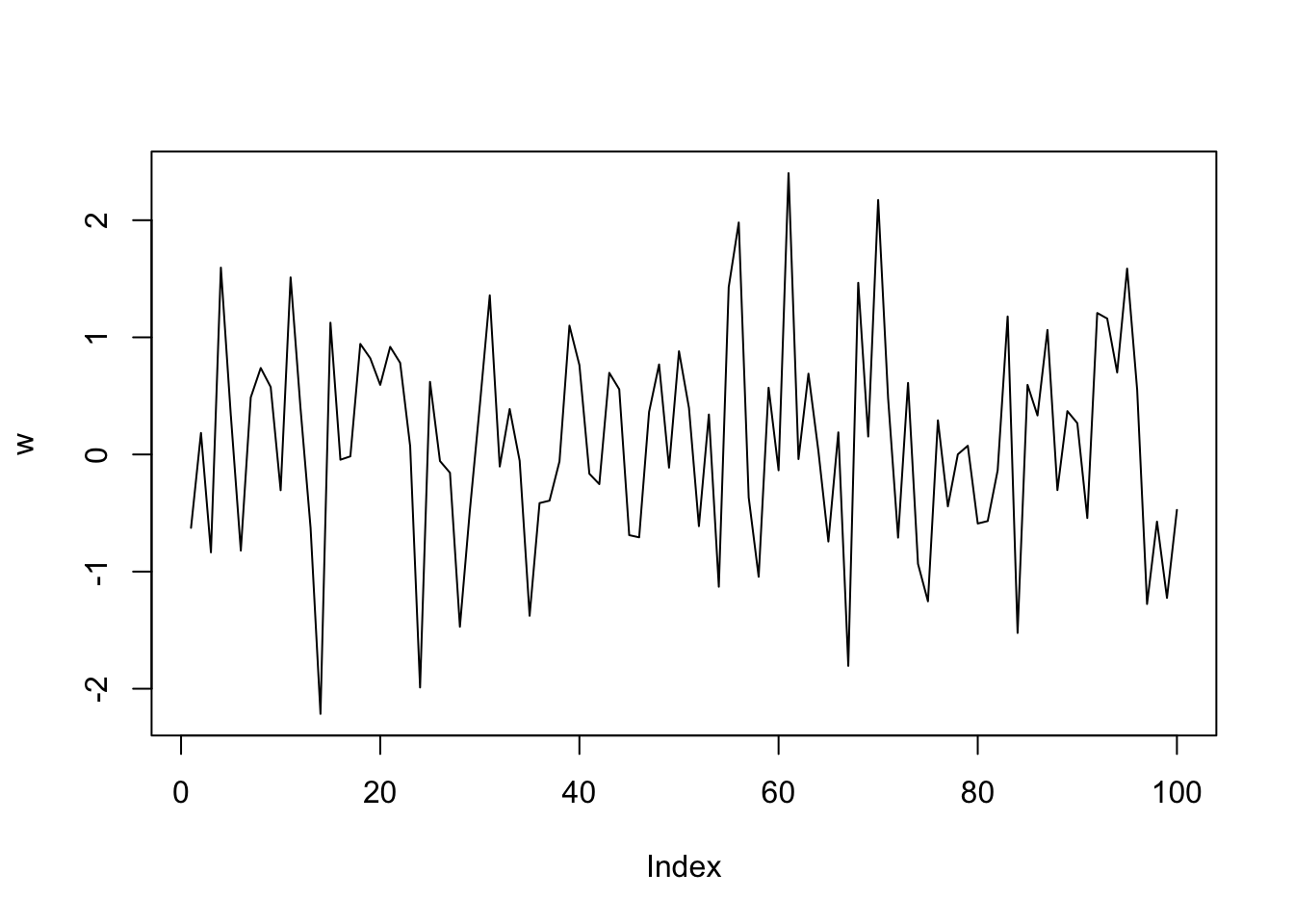
Chapter 4: Basic Stochastic Models

Throughout this book, we will often fit models to data that we have simulated and attempt to recover the underlying model parameters. At first sight, this might seem odd, given that the parameters are used to simulate the data so that we already know at the outset the values the parameters should take. However, the procedure is useful for a number of reasons. In particular, to be able to simulate data using a model requires that the model formulation be correctly understood. If the model is understood but incorrectly implemented, then the parameter estimates from the fitted model may deviate significantly from the underlying model values used in the simulation. Simulation can therefore help ensure that the model is both correctly understood and correctly implemented.

4.2.3 “Simulation in R” Modern Look

Book code

set.seed(1)
w <- rnorm(100)
plot(w, type = "l")

Tidyverts code

pacman::p_load("tsibble", "fable", "feasts",
    "tsibbledata", "fable.prophet", "tidyverse", "patchwork")
set.seed(1)
wd <- tibble(
    x = 1:100,
    y = rnorm(100))
wd |> ggplot(aes(x = x, y = y)) + geom_line()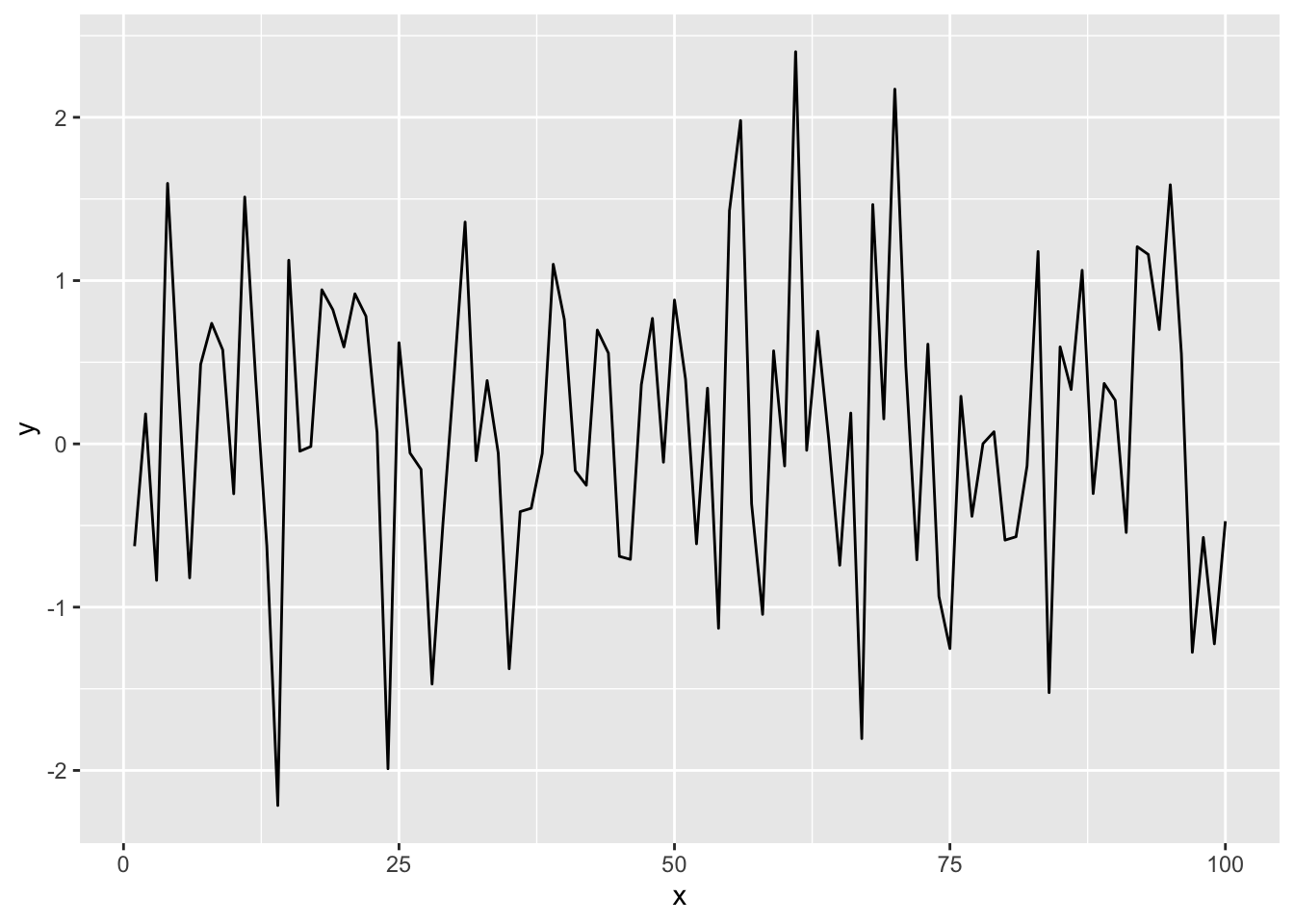

x <- seq(-3, 3, length = 1000)
hist(rnorm(100), prob = T)
points(x, dnorm(x), type = "l")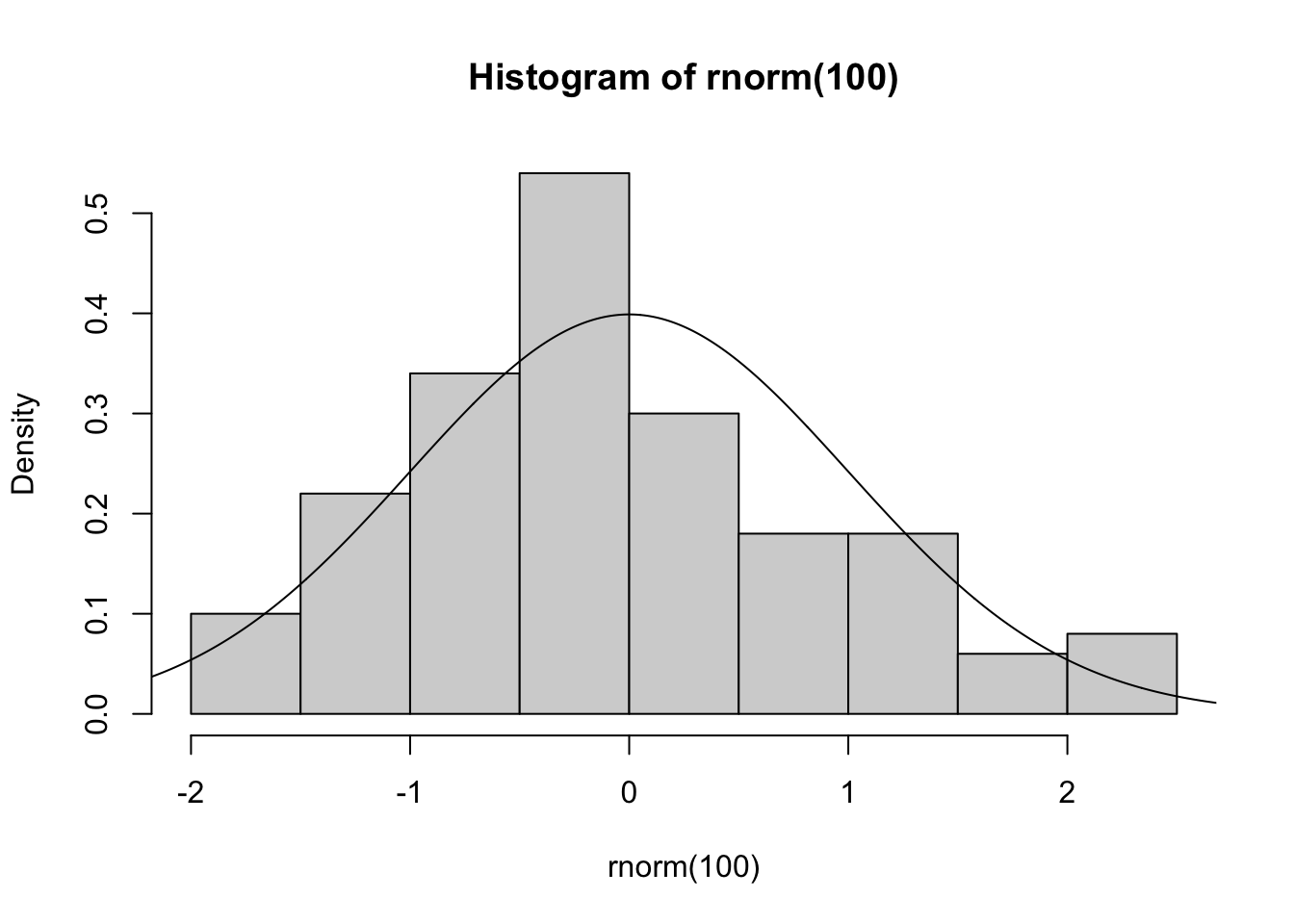

xd <- tibble(
    x = seq(-3, 3, length = 1000),
    norm = rnorm(1000),
    density = dnorm(x)
)
xd |>
    ggplot(aes(x = norm)) +
    geom_histogram(aes(y = after_stat(density)),
        color = "white", fill = "darkgrey") +
    geom_line(aes(x = x, y = density)) +
    theme_bw()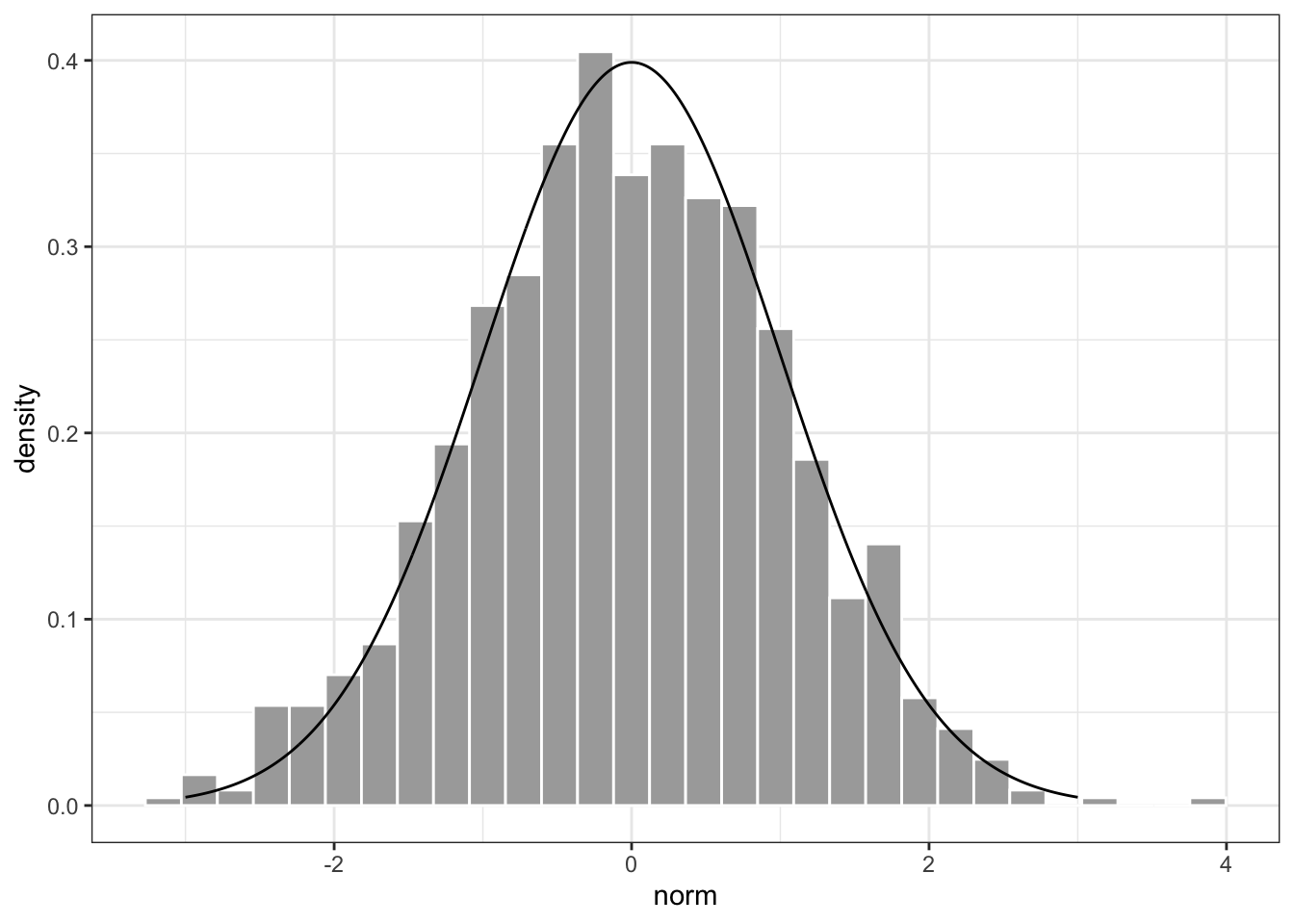

Show the Book code in full 
set.seed(1)
w <- rnorm(100)
plot(w, type = "l")
x <- seq(-3,3, length = 1000)
hist(rnorm(100), prob = T); points(x, dnorm(x), type = "l")
Show the Tidyverts code in full 
set.seed(1)
wd <- tibble(
    x = 1:100,
    y = rnorm(100))
wd |> ggplot(aes(x = x, y = y)) + geom_line()
xd <- tibble(
    x = seq(-3, 3, length = 1000),
    norm = rnorm(1000),
    density = dnorm(x)
)
xd |>
    ggplot(aes(x = norm)) +
    geom_histogram(aes(y = after_stat(density)),
        color = "white", fill = "darkgrey") +
    geom_line(aes(x = x, y = density)) +
    theme_bw()

4.2.4 “Second-order properties and the correlogram” Modern Look

Book code

set.seed(2)
acf(rnorm(100))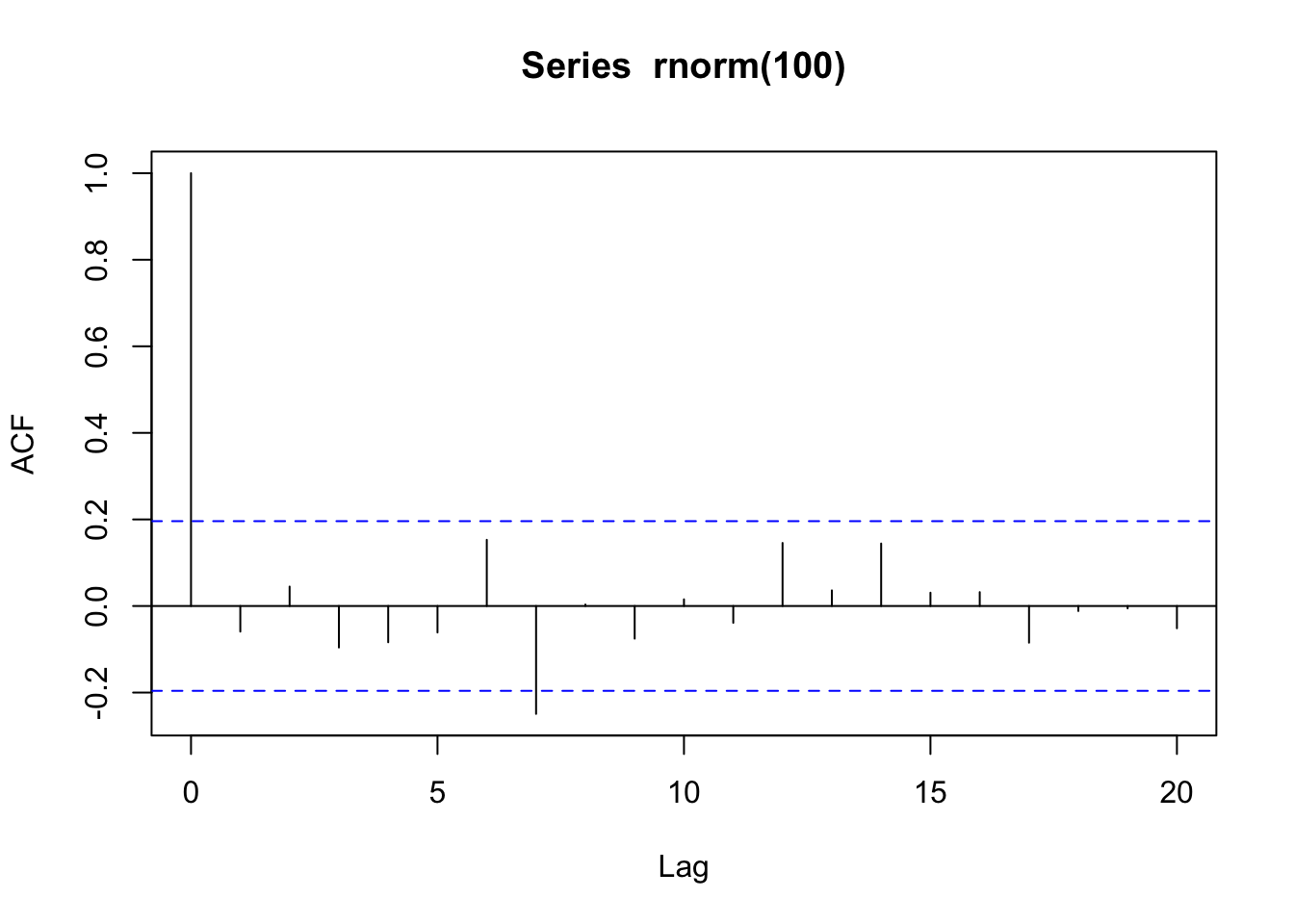

Tidyverts code

set.seed(2)
tsibble(seq = 1:100,
        values = rnorm(100),
        index = seq) |>
    ACF(values) |>
    autoplot()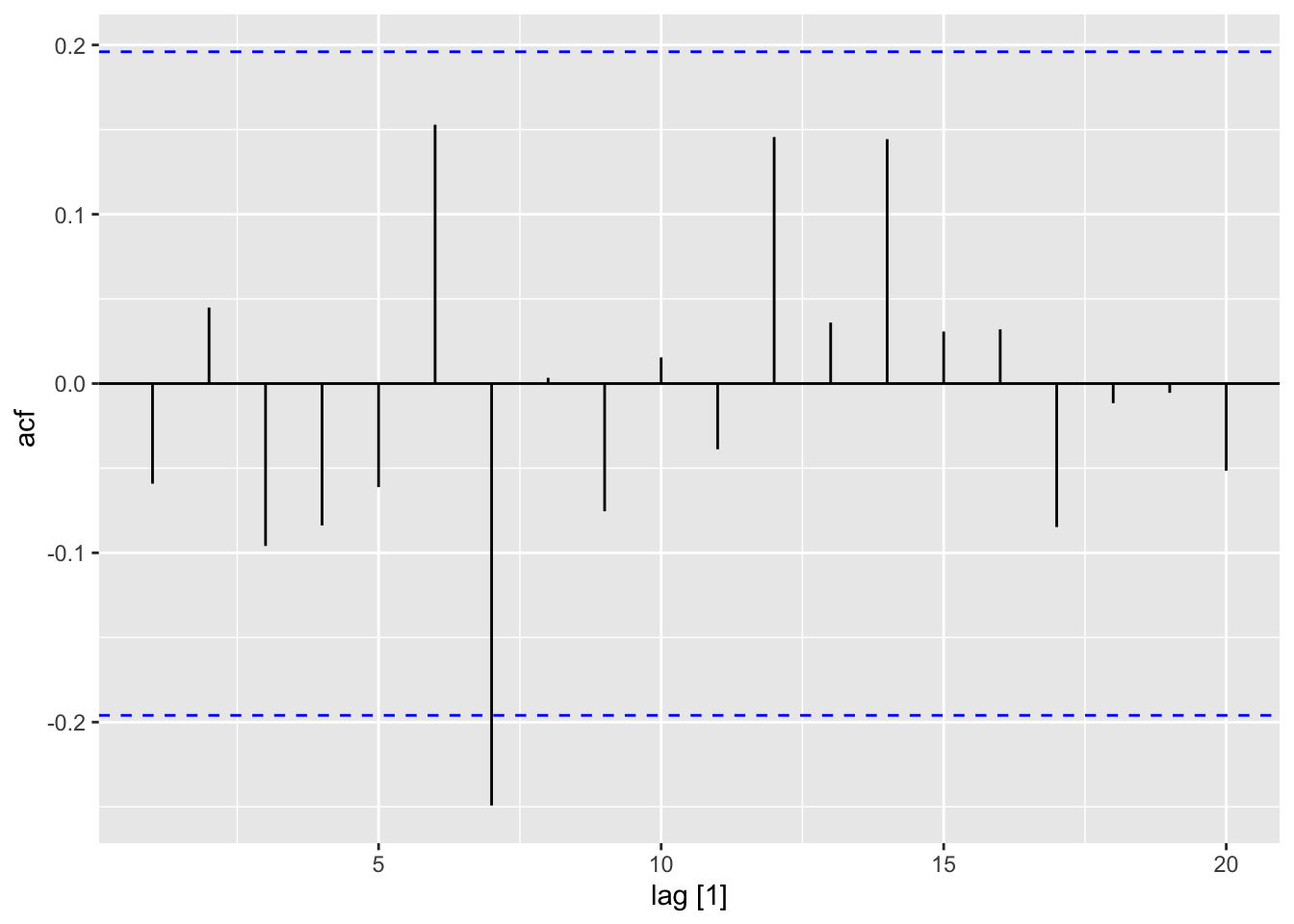

4.3.7 “Simulation” Modern Look

Book code

set.seed(2)
x <- w <- rnorm(1000)
for (t in 2:1000) x[t] <- x[t - 1] + w[t]
plot(x, type = "l")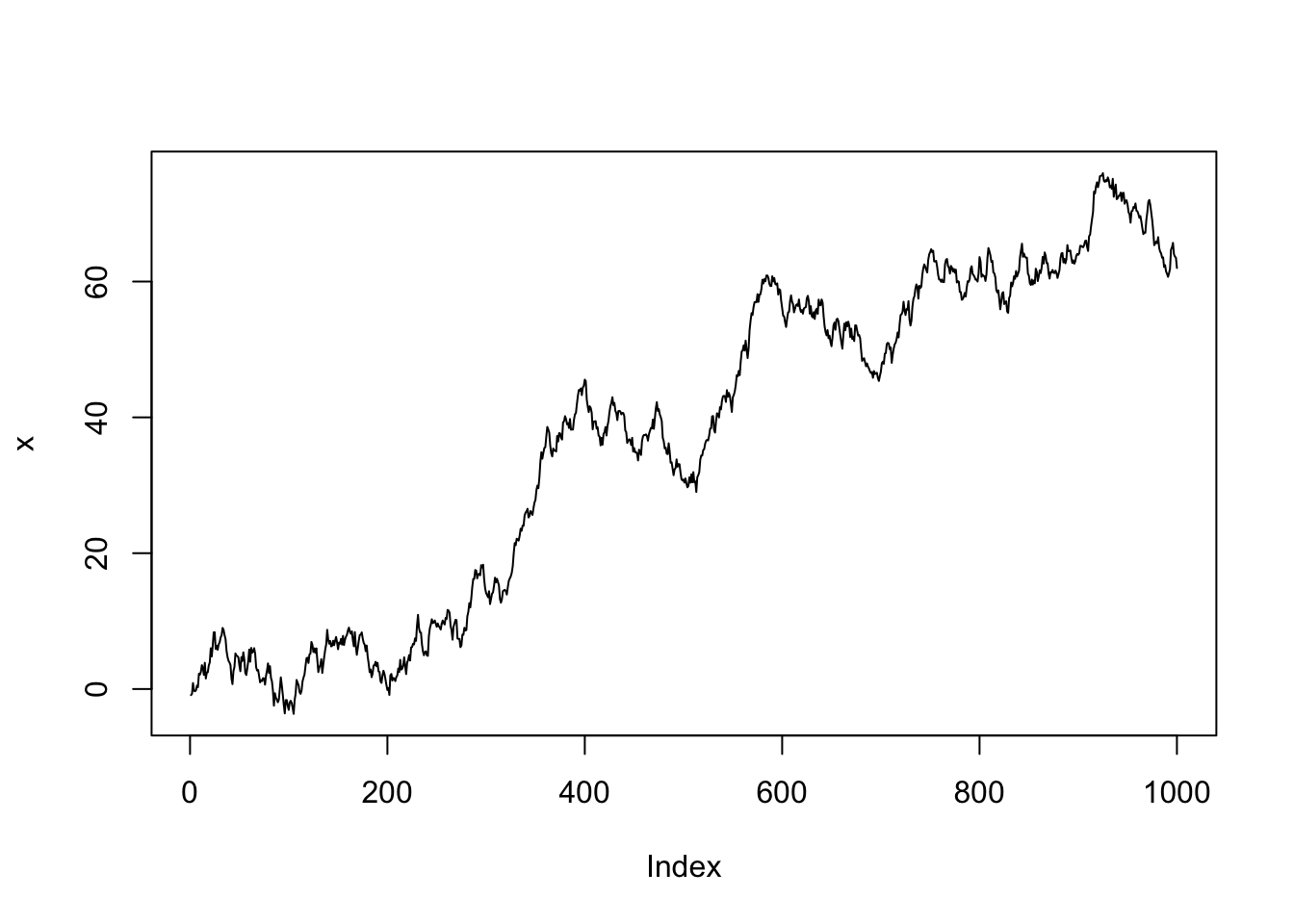

Tidyverts code

set.seed(2)
dat <- tibble(w = rnorm(1000)) |>
    mutate(
        index = 1:n(),
         x = purrr::accumulate2(
            lag(w), w, 
            \(acc, nxt, w) acc + w,
            .init = 0)[-1]) |>
    tsibble::as_tsibble(index = index)
autoplot(dat, .var = x)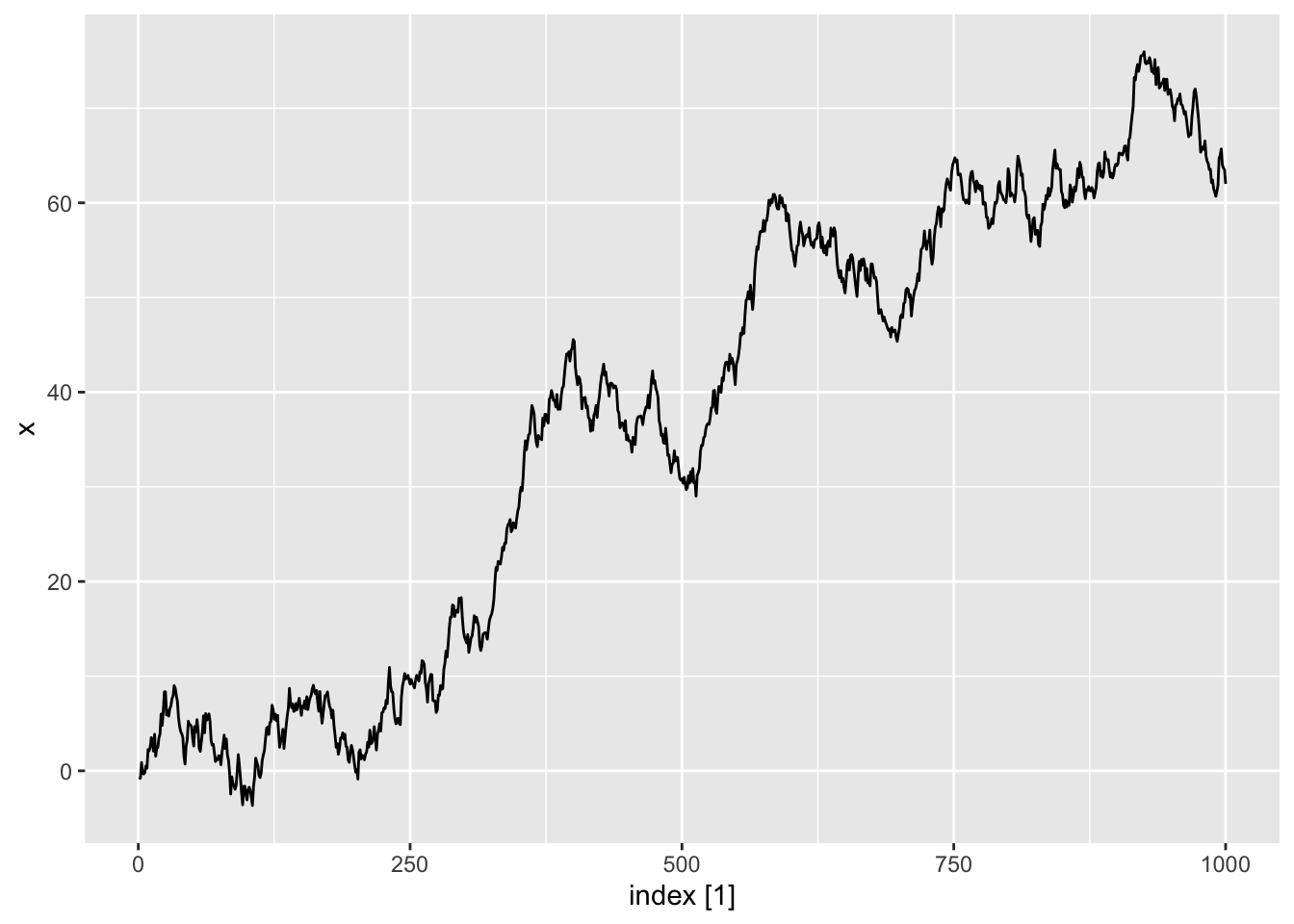

acf(x)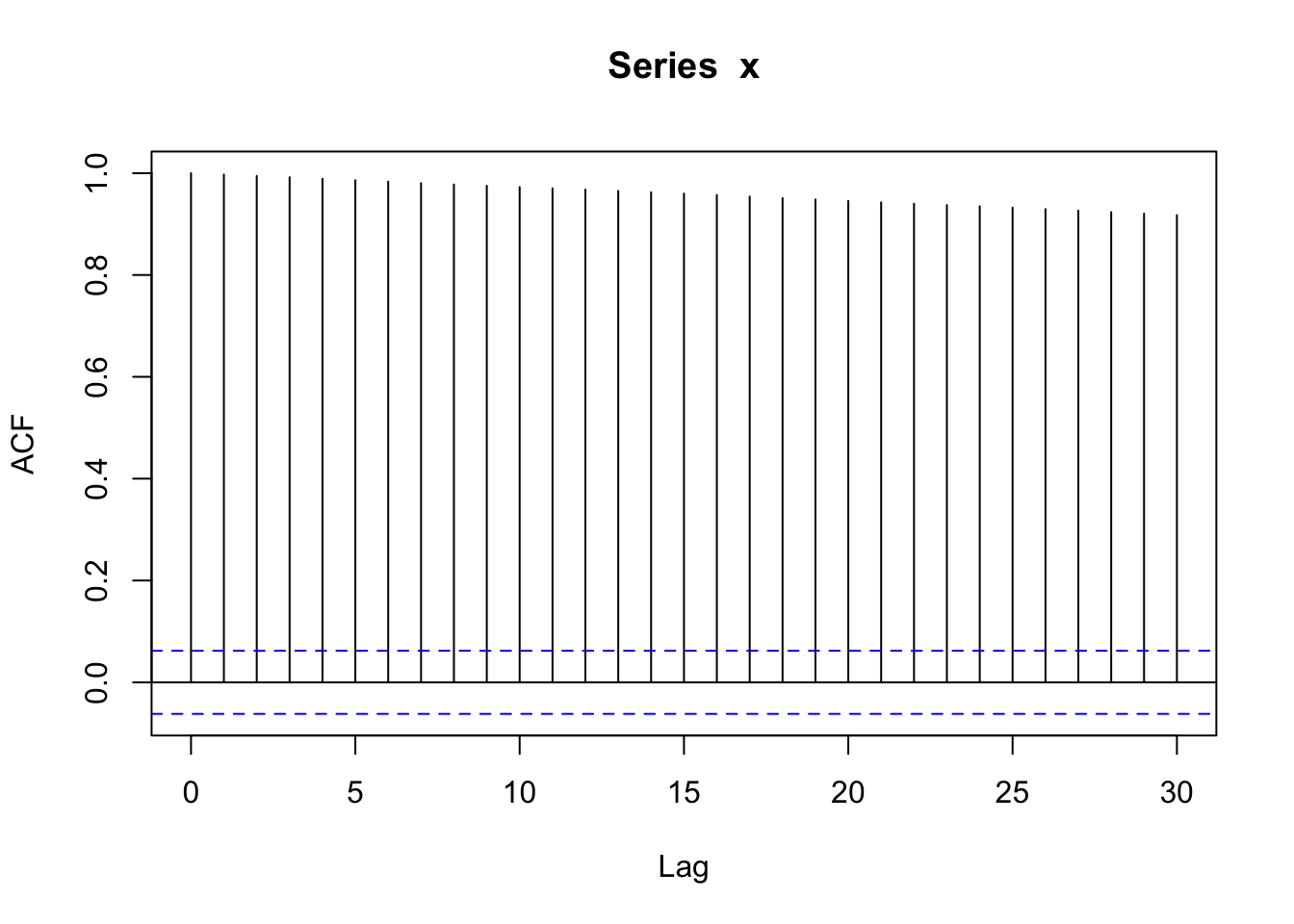

ACF(dat, x) |>
    autoplot()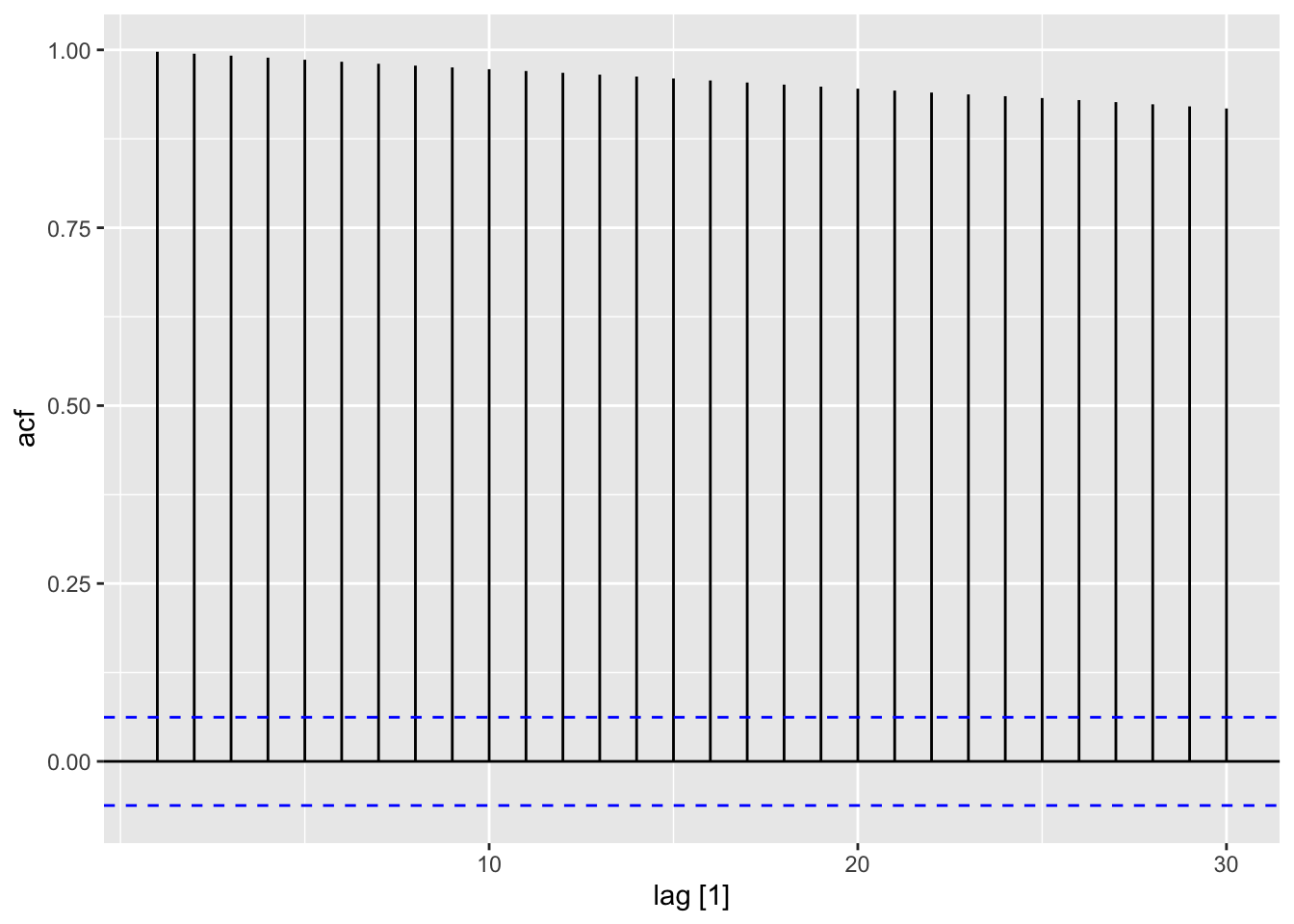

Show the Book code in full 
x <- w <- rnorm(1000)
for (t in 2:1000) x[t] <- x[t - 1] + w[t]
plot(x, type = "l")
acf(x)
Show the Tidyverts code in full 
set.seed(2)
dat <- tibble(w = rnorm(1000)) |>
    mutate(
        index = 1:n(),
         x = purrr::accumulate2(
            lag(w), w, 
            \(acc, nxt, w) acc + w,
            .init = 0)[-1]) |>
    tsibble::as_tsibble(index = index)
autoplot(dat, .var = x)
ACF(dat, x) |>
    autoplot()

4.4.1 “Simulated random walk series” Modern Look

Book code

acf(diff(x))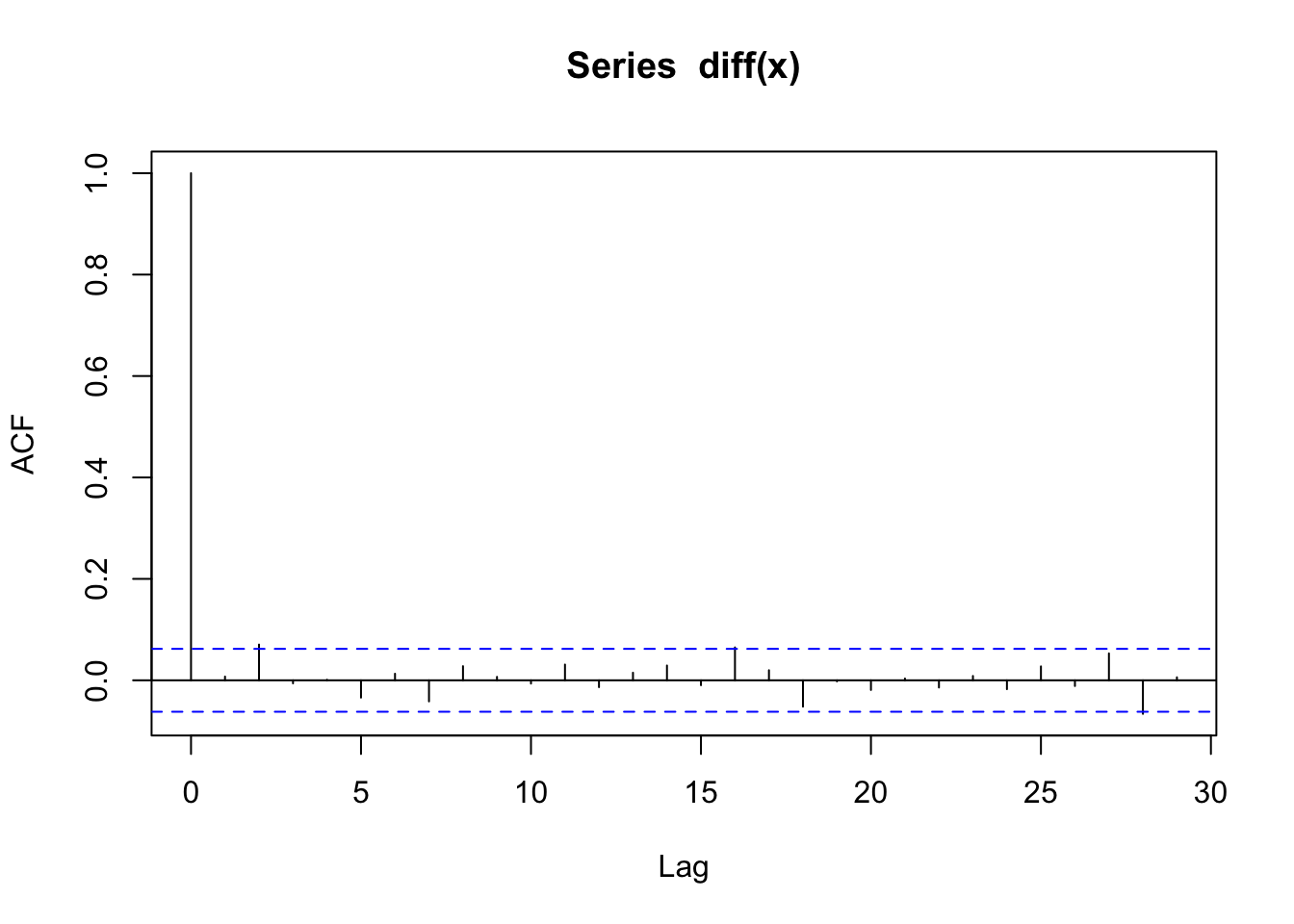

Tidyverts code

dat |>
    mutate(diff = x - lag(x)) |>
    ACF(diff) |>
    autoplot()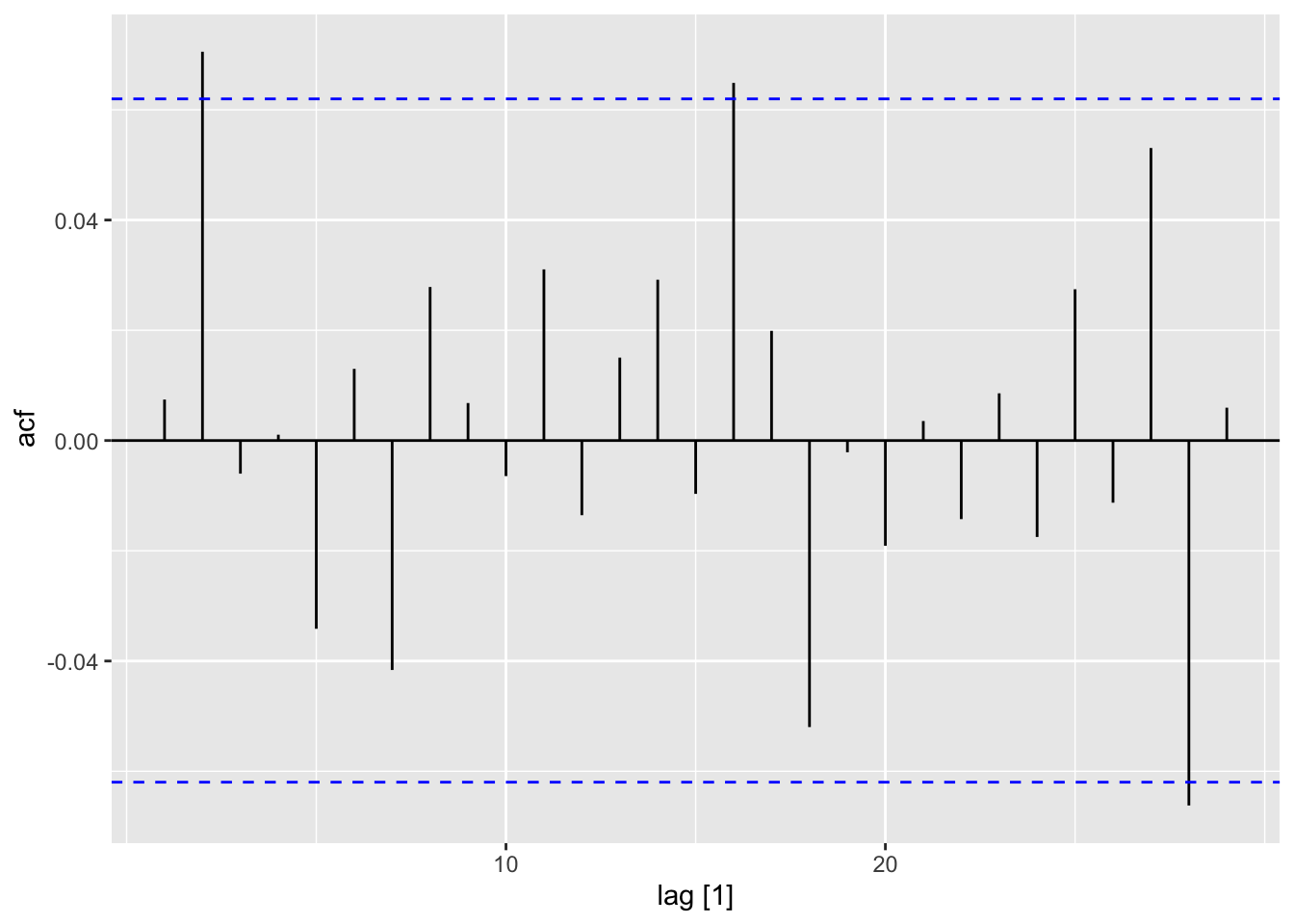

4.4.2 “Exchange rate series” Modern Look

Book code

Z <- read.table("data/pounds_nz.dat", header = T)
Z.ts <- ts(Z, st = 1991, fr = 4)
acf(diff(Z.ts))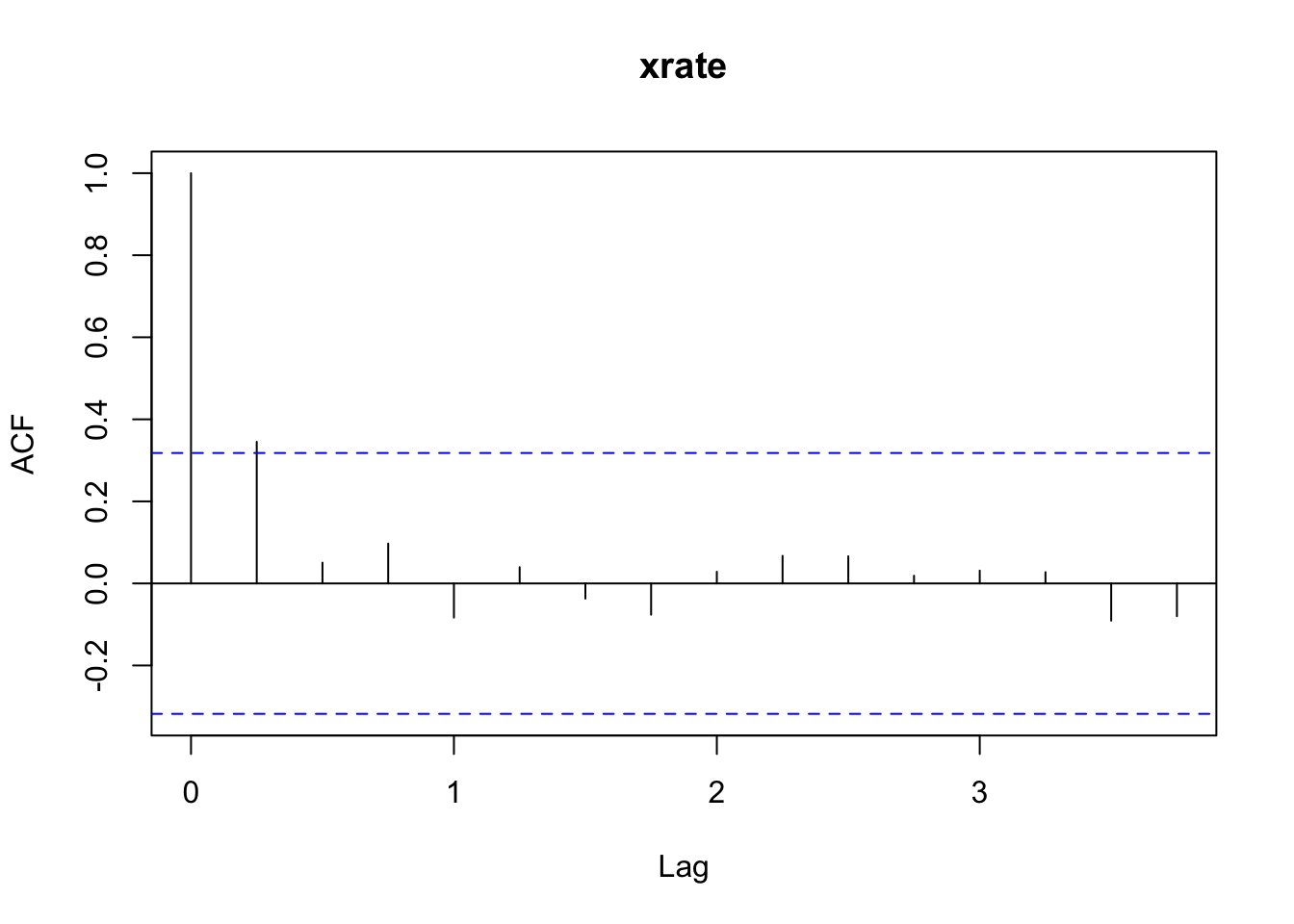

Tidyverts code

z <- read_table("data/pounds_nz.dat")
date_seq <- seq(
    lubridate::ymd("1991-01-01"),
    by = "3 months",
    length.out = nrow(z))
z_ts <- z |>
    mutate(
        date = date_seq,
        quarter = tsibble::yearquarter(date)) |>
    as_tsibble(index = quarter)
z_ts |>
    mutate(diff = xrate - lag(xrate)) |>
    ACF(diff) |>
    autoplot()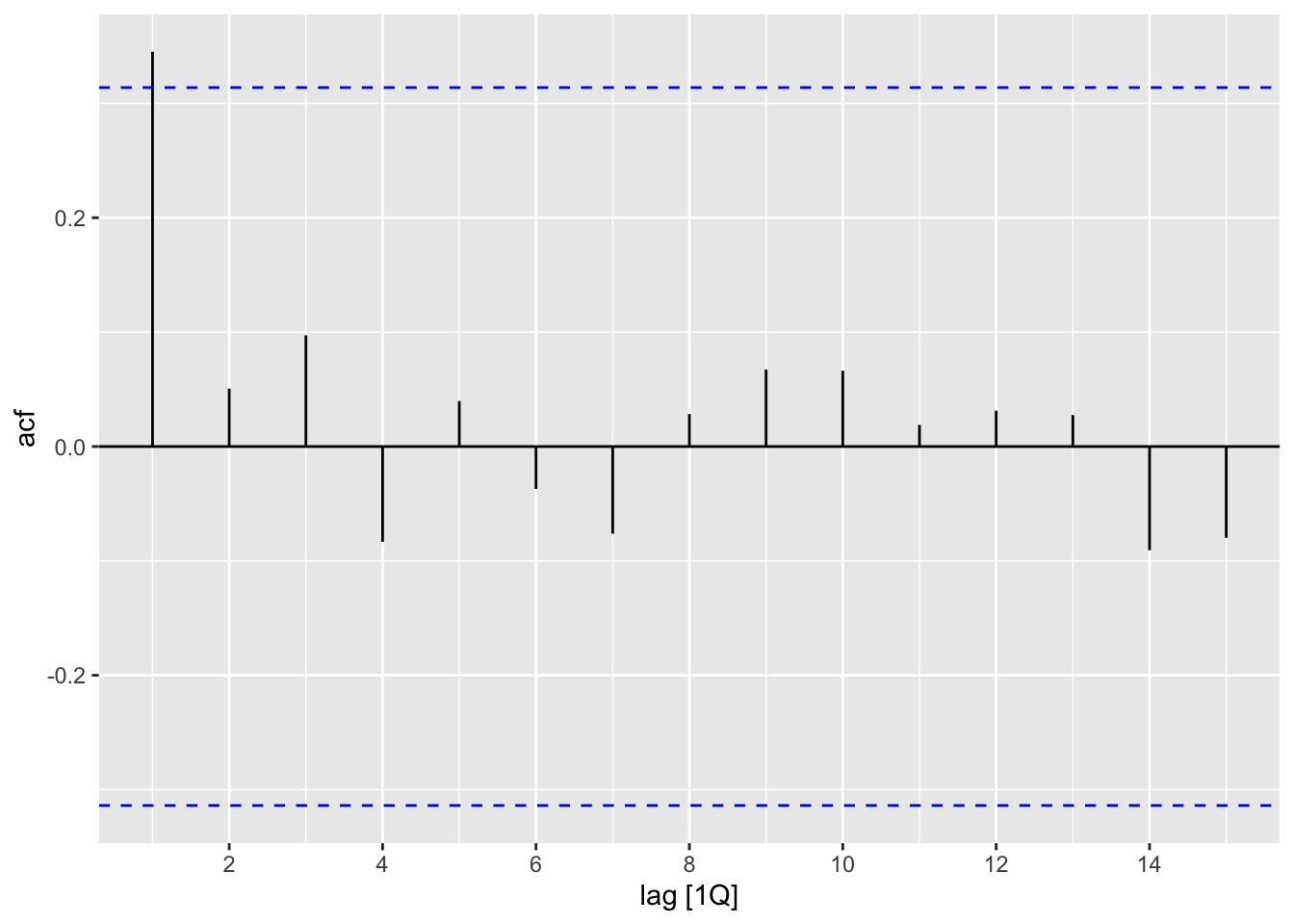

Z.hw <- HoltWinters(Z.ts, alpha = 1, gamma = FALSE) # changed from book
acf(resid(Z.hw)) # not exact match.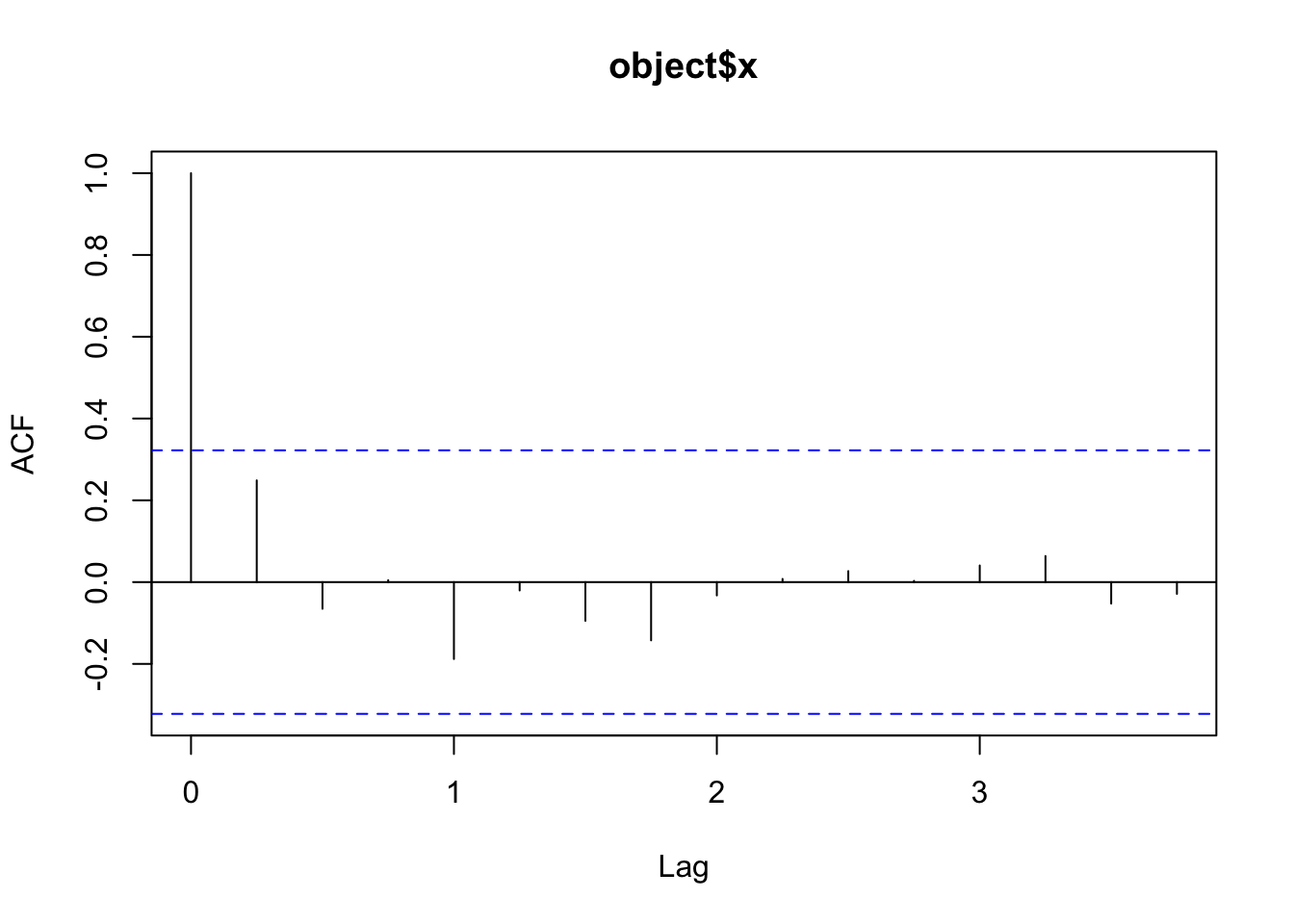

z_hw <- z_ts |>
    model(Additive = ETS(xrate ~
        trend("A", alpha = 1) +
        error("A") + season("N", gamma = 0),
        opt_crit = "amse", nmse = 1)) |>
        residuals()
ACF(z_hw, .resid) |>
    autoplot()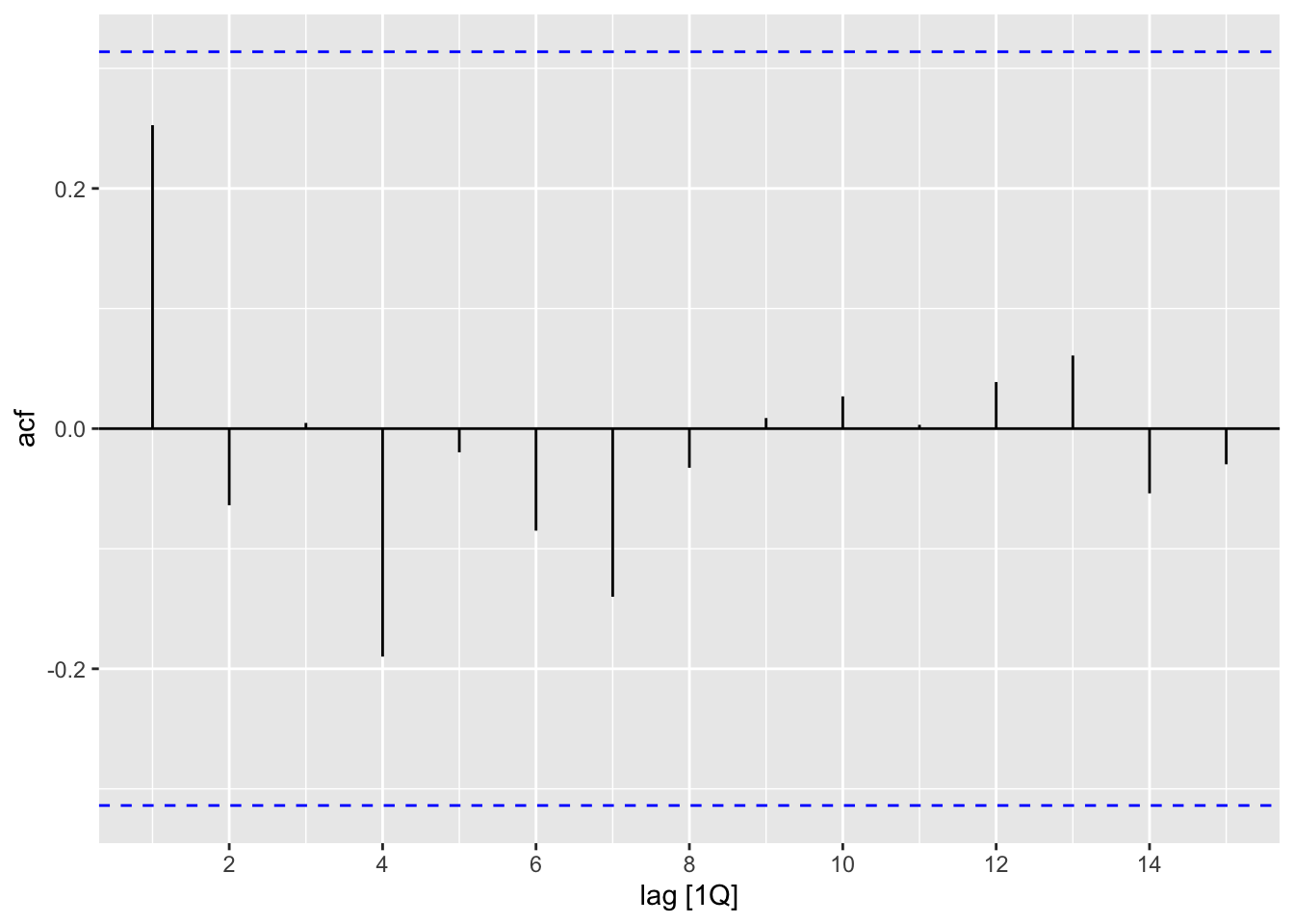

Show the Book code in full 
Z <- read.table("data/pounds_nz.dat", header = T)
Z.ts <- ts(Z, st = 1991, fr = 4)
acf(diff(Z.ts))
Z.hw <- HoltWinters(Z.ts, alpha = 1, gamma = FALSE) # changed from book
acf(resid(Z.hw)) # not exact match.
Show the Tidyverts code in full 
z <- read_table("data/pounds_nz.dat")
date_seq <- seq(
    lubridate::ymd("1991-01-01"),
    by = "3 months",
    length.out = nrow(z))
z_ts <- z |>
    mutate(
        date = date_seq,
        quarter = tsibble::yearquarter(date)) |>
    as_tsibble(index = quarter)
z_ts |>
    mutate(diff = xrate - lag(xrate)) |>
    ACF(diff) |>
    autoplot()
z_hw <- z_ts |>
    model(Additive = ETS(xrate ~
        trend("A", alpha = 1) +
        error("A") + season("N", gamma = 0),
        opt_crit = "amse", nmse = 1)) |>
        residuals()
ACF(z_hw, .resid) |>
    autoplot()

4.4.3 “Random walk with drift” data Modern Look

Book code

HP.dat <- read.table("data/HP.txt", header = T)
# attach(HP.dat) # bad practice
plot(as.ts(HP.dat$Price))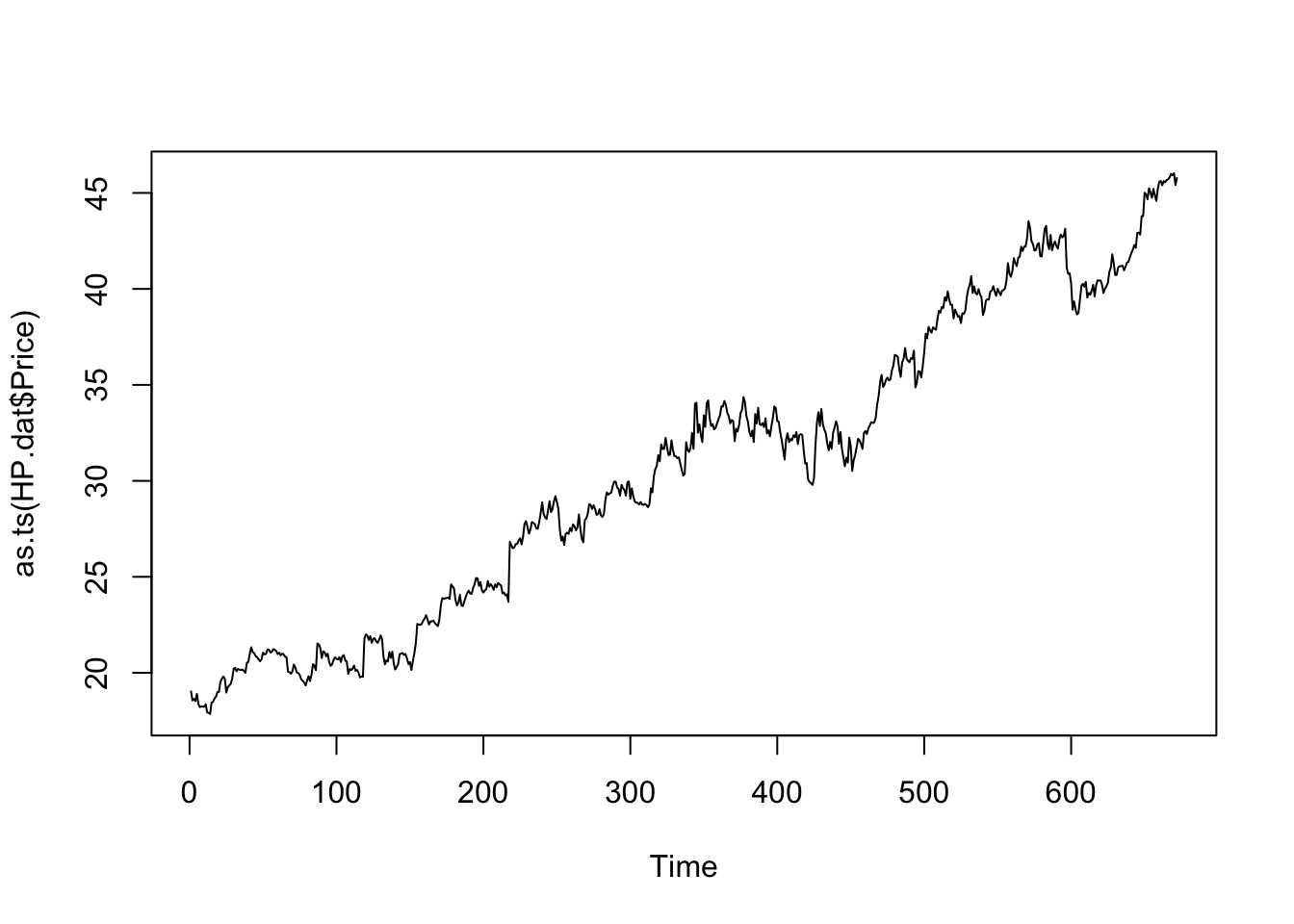

Tidyverts code

hp_dat <- read_table("data/HP.txt") |>
    mutate(Day = 1:n())
ggplot(hp_dat, aes(x = Day, y = Price)) + geom_line()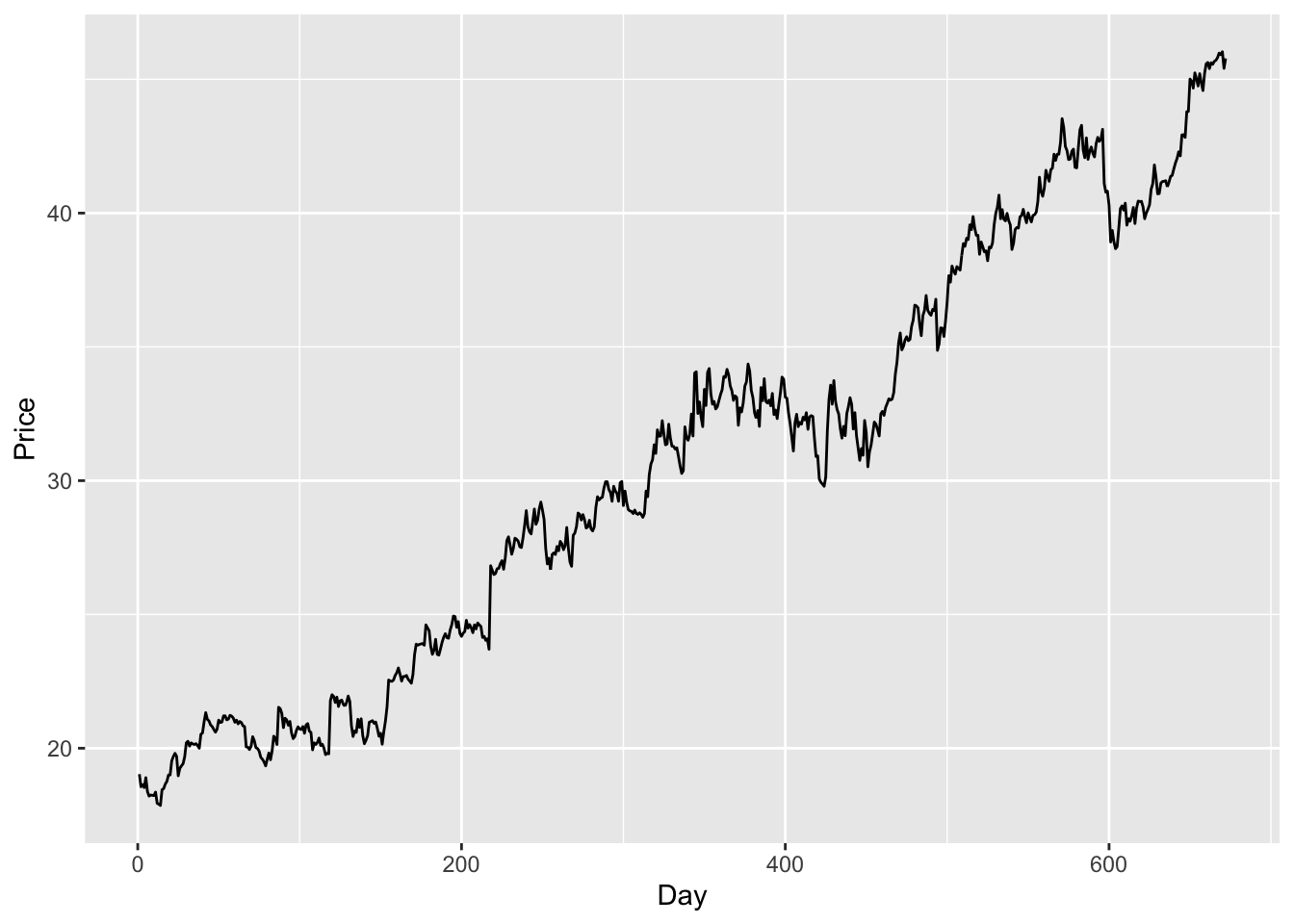

DP <- diff(HP.dat$Price)
plot(as.ts(DP))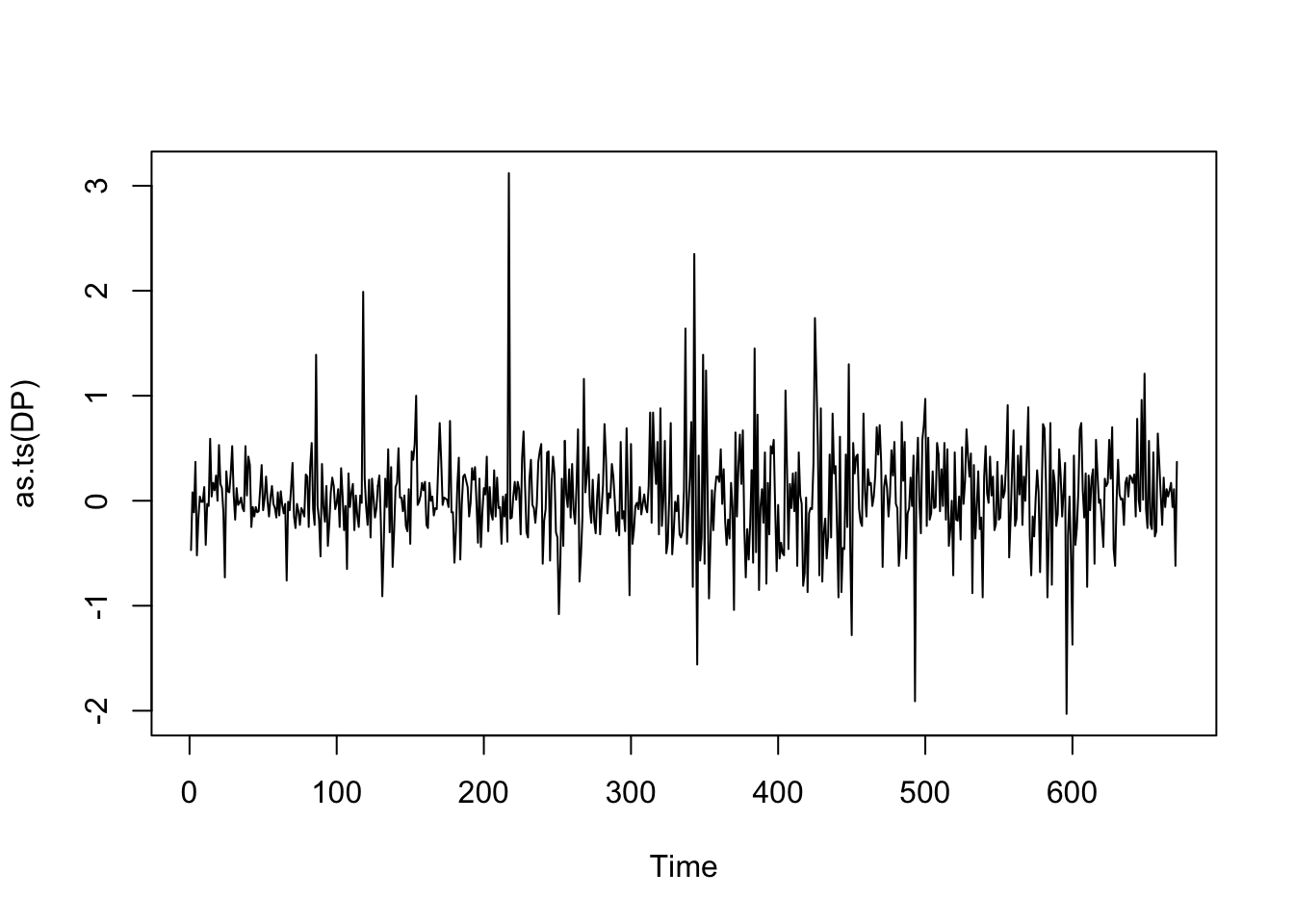

hp_dat |>
    mutate(diff = Price - lag(Price)) |>
ggplot(aes(x = Day, y = diff)) +
    geom_line()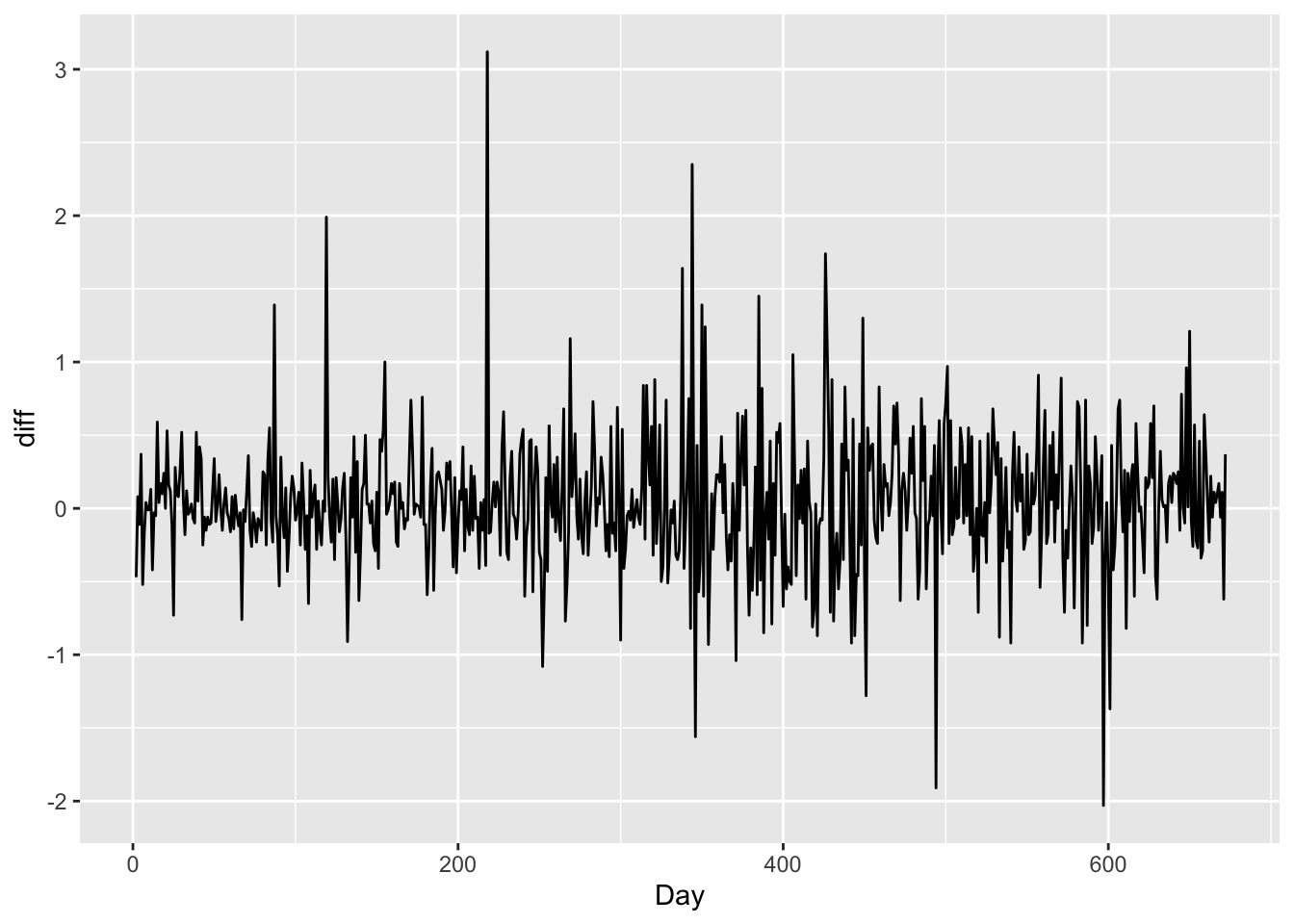

acf(DP)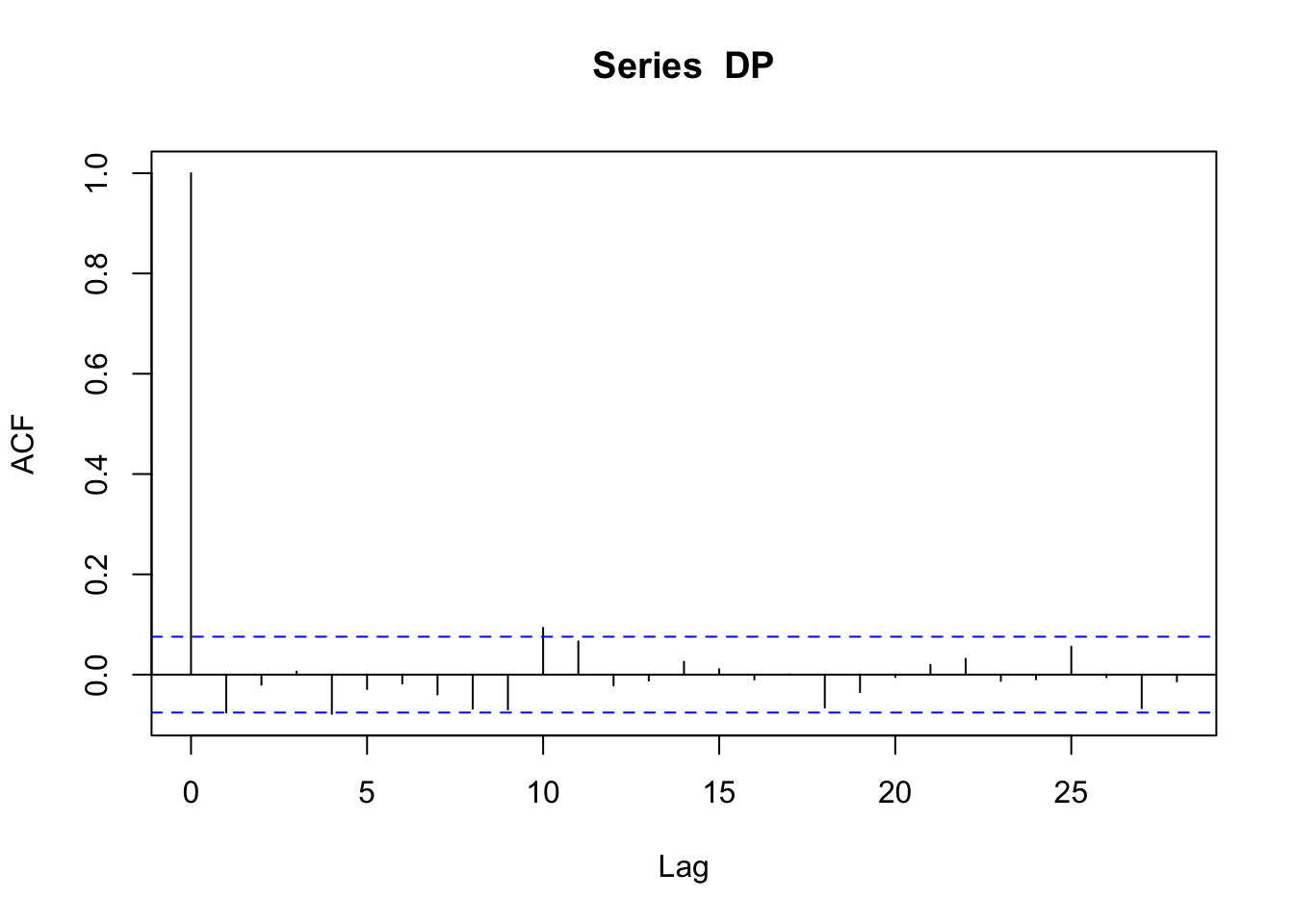

hp_dat |>
    mutate(diff = Price - lag(Price)) |>
    as_tsibble(index = Day) |>
ACF(diff) |>
    autoplot()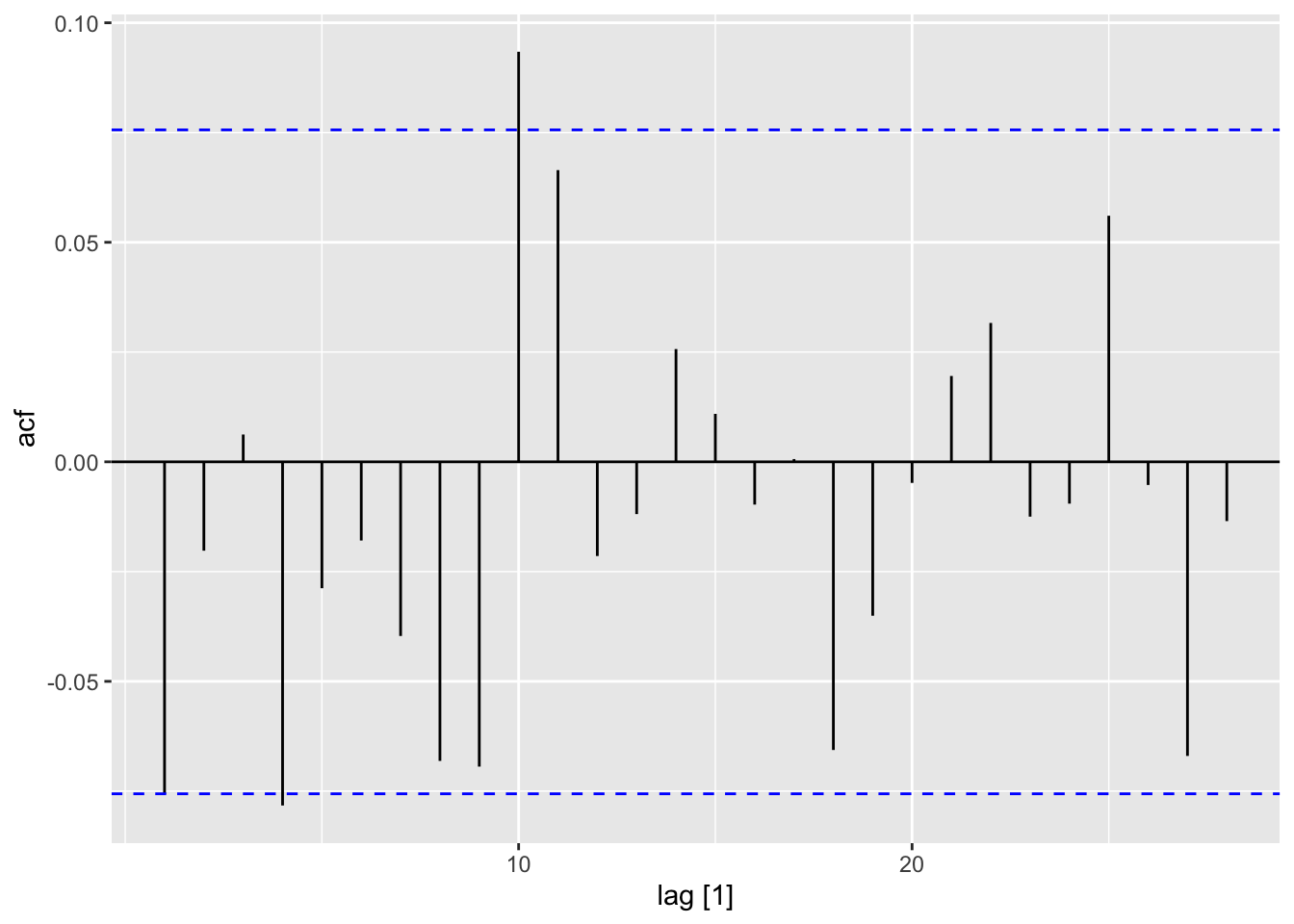

mean(DP) + c(-2, 2) * sd(DP) / sqrt(length(DP))
[1] 0.004378275 0.075353468
hp_dat |>
    mutate(diff = Price - lag(Price)) |>
    slice(-1) |>
    summarize(
        mean = mean(diff),
        sd = sd(diff),
        n = n(),
        std_error = sd / sqrt(n),
        lower = mean - 2 * std_error,
        upper = mean + 2 * std_error)
# A tibble: 1 × 6
    mean    sd     n std_error   lower  upper
   <dbl> <dbl> <int>     <dbl>   <dbl>  <dbl>
1 0.0399 0.460   671    0.0177 0.00438 0.0754
Show the Book code in full 
HP.dat <- read.table("data/HP.txt", header = T)
# attach(HP.dat) # bad practice
plot(as.ts(HP.dat$Price))
DP <- diff(HP.dat$Price)
plot(as.ts(DP))
acf(DP)
mean(DP) + c(-2, 2) * sd(DP) / sqrt(length(DP))
Show the Tidyverts code in full 
hp_dat <- read_table("data/HP.txt") |>
    mutate(Day = 1:n())
ggplot(hp_dat, aes(x = Day, y = Price)) 
     geom_line()

hp_dat |>
    mutate(diff = Price - lag(Price)) |>
ggplot(aes(x = Day, y = diff)) +
    geom_line()

hp_dat |>
    mutate(diff = Price - lag(Price)) |>
    as_tsibble(index = Day) |>
ACF(diff) |>
    autoplot()

hp_dat |>
    mutate(diff = Price - lag(Price)) |>
    slice(-1) |>
    summarize(
        mean = mean(diff),
        sd = sd(diff),
        n = n(),
        std_error = sd / sqrt(n),
        lower = mean - 2 * std_error,
        upper = mean + 2 * std_error)

4.5.7 Autoregressive “Simulation” Modern Look

Book code

rho <- function(k, alpha) alpha^k
layout(1:2)
plot(0:10, rho(0:10, 0.7), type = "b")
plot(0:10, rho(0:10, -0.7), type = "b")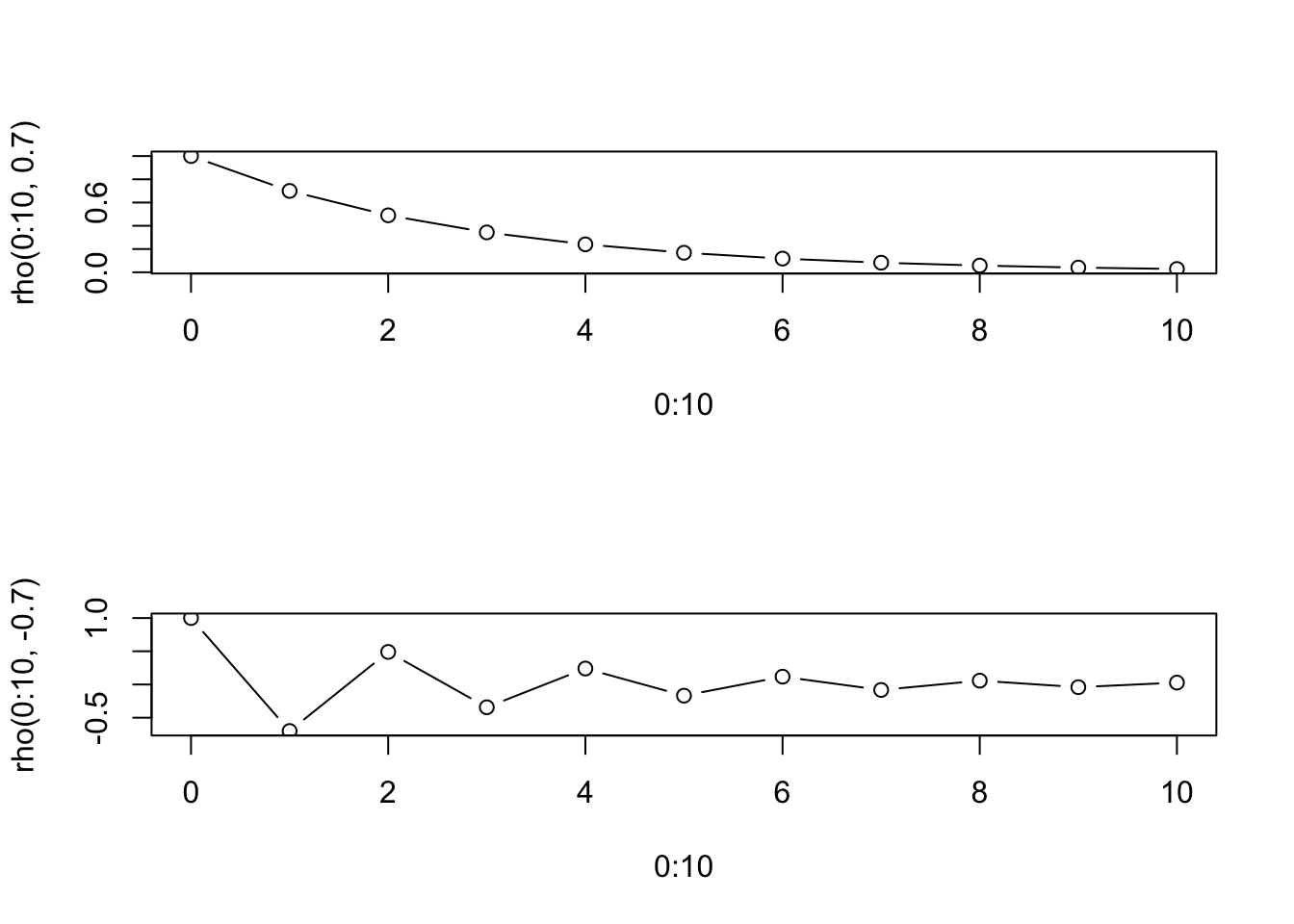

Tidyverts code

rho <- function(k, alpha) alpha^k
dat <- tibble(
        x = 0:10,
        a7 = rho(x, .7),
        am7 = rho(x, -.7)) |>
    pivot_longer(a7:am7,
        names_to = "param",
        values_to = "value") 

ggplot(dat, aes(x = x, y = value)) +
    geom_line() +
    geom_point() +
    facet_wrap(~param, ncol = 1)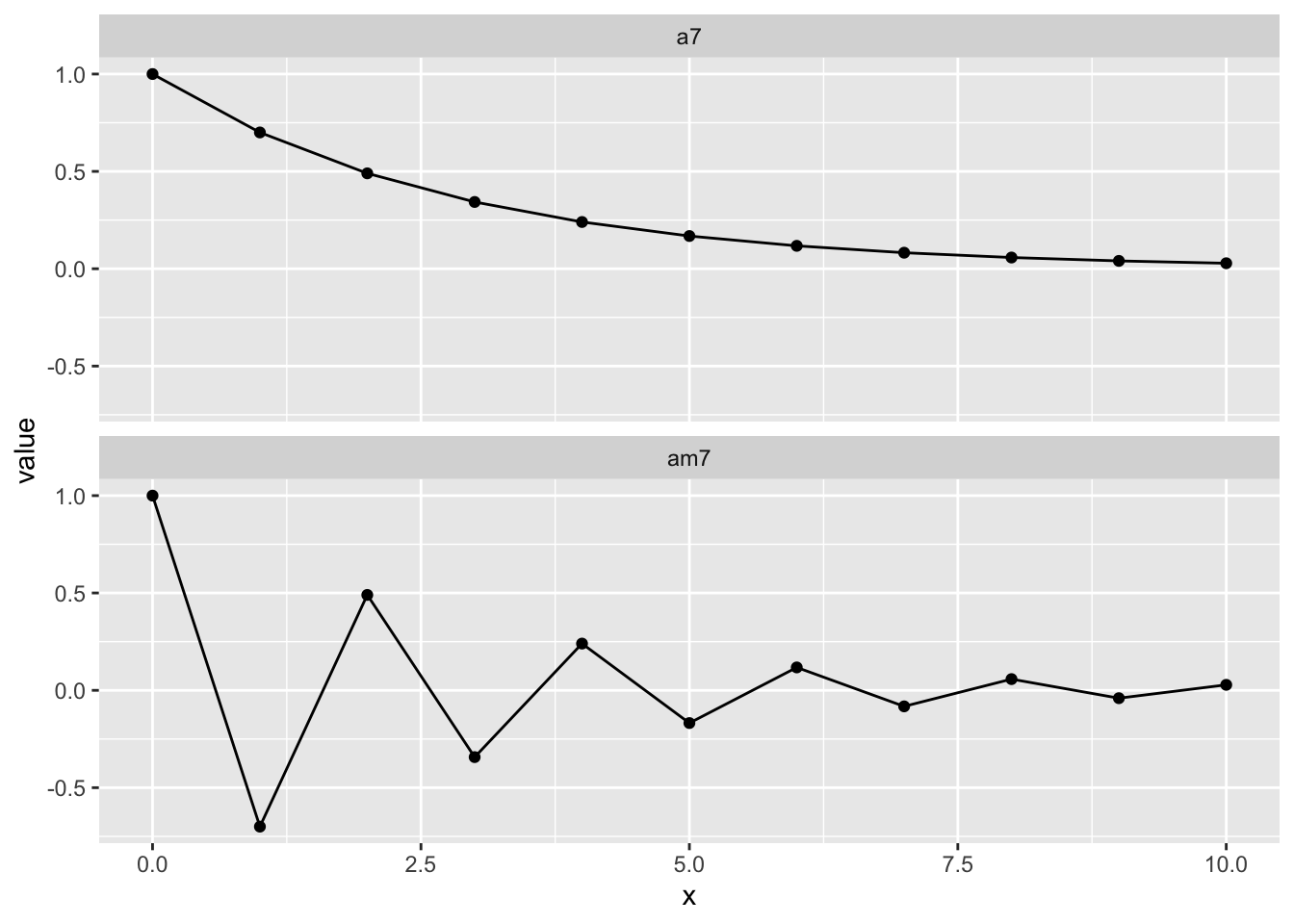

set.seed(1)
x <- w <- rnorm(100)
for (t in 2:100) x[t] <- 0.7 * x[t - 1] + w[t]
plot(x, type = "l")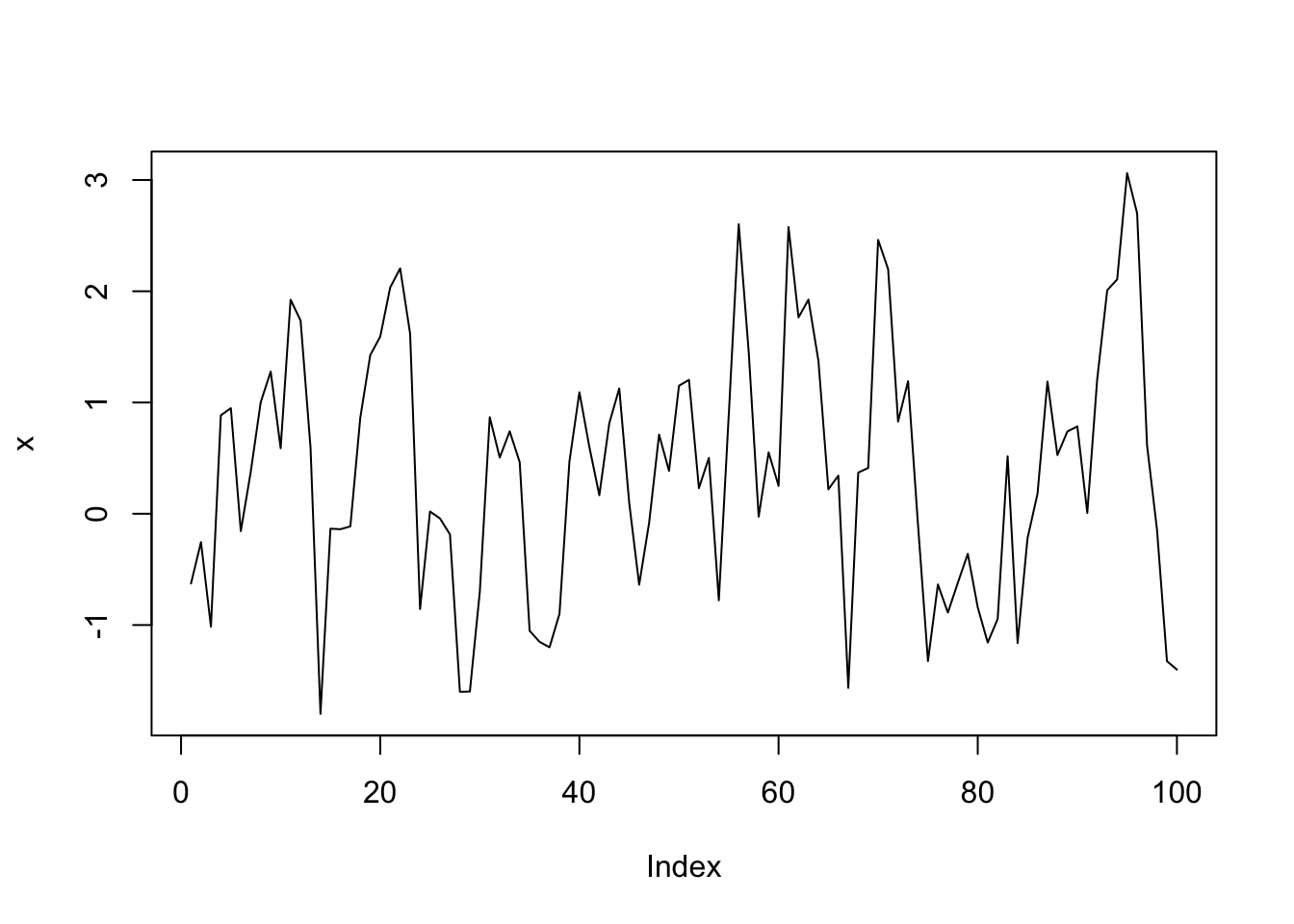

set.seed(1)
dat <- tibble(w = rnorm(100)) |>
    mutate(
        index = 1:n(),
         x = purrr::accumulate2(
            lag(w), w, 
            \(acc, nxt, w) 0.7 * acc + w,
            .init = 0)[-1]) |>
    tsibble::as_tsibble(index = index)
autoplot(dat, .var = x)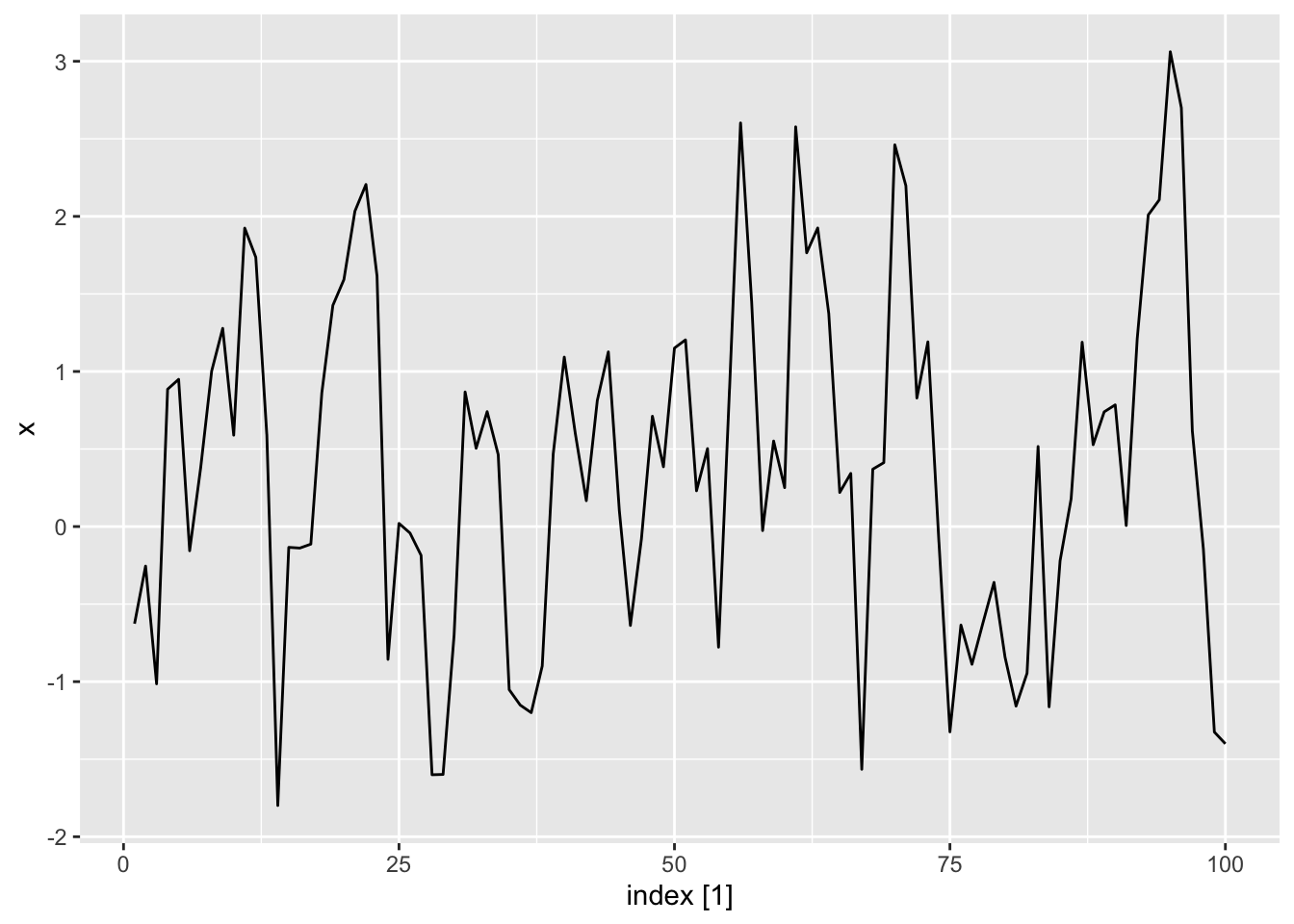

acf(x)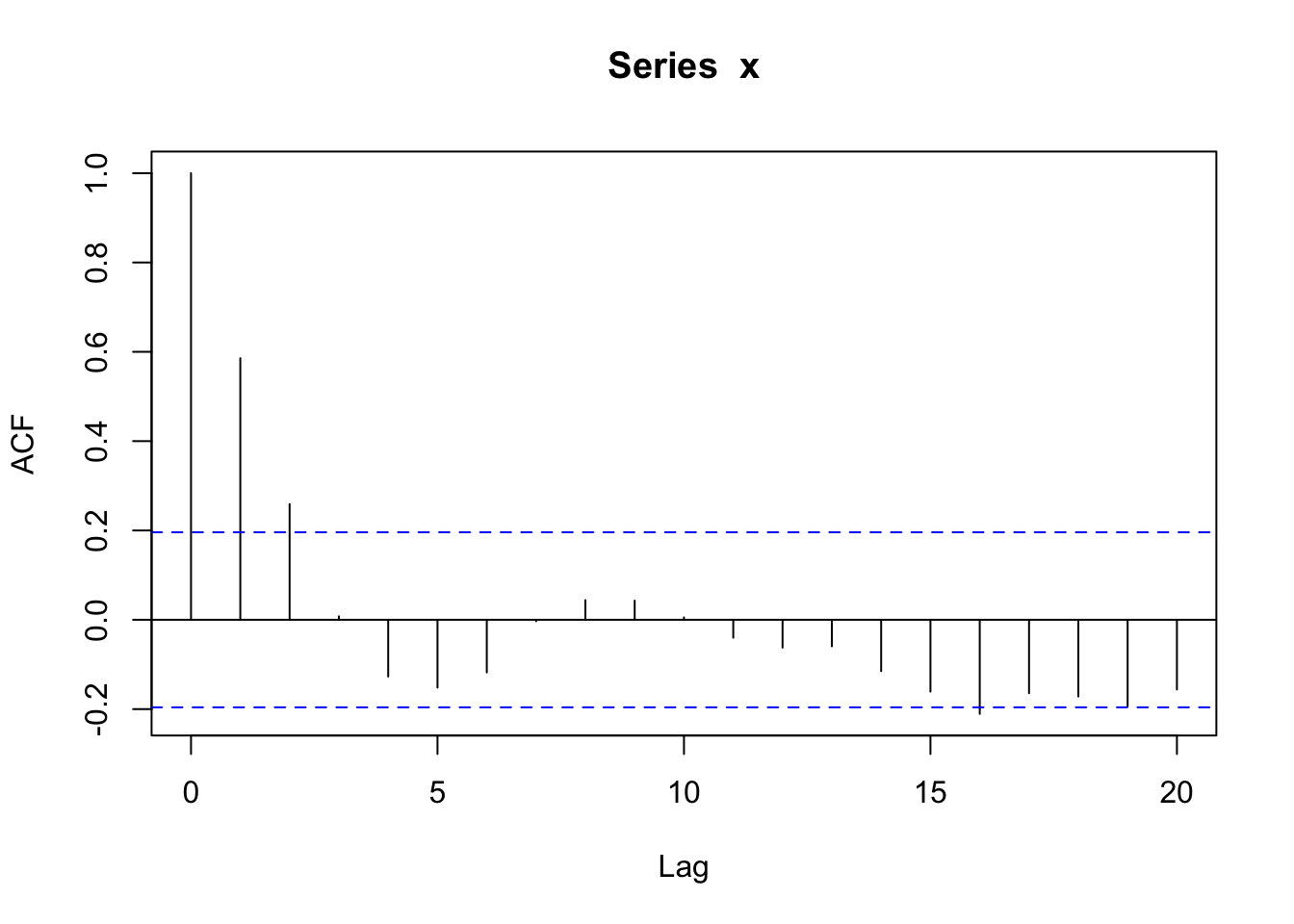

ACF(dat, x) |>
    autoplot()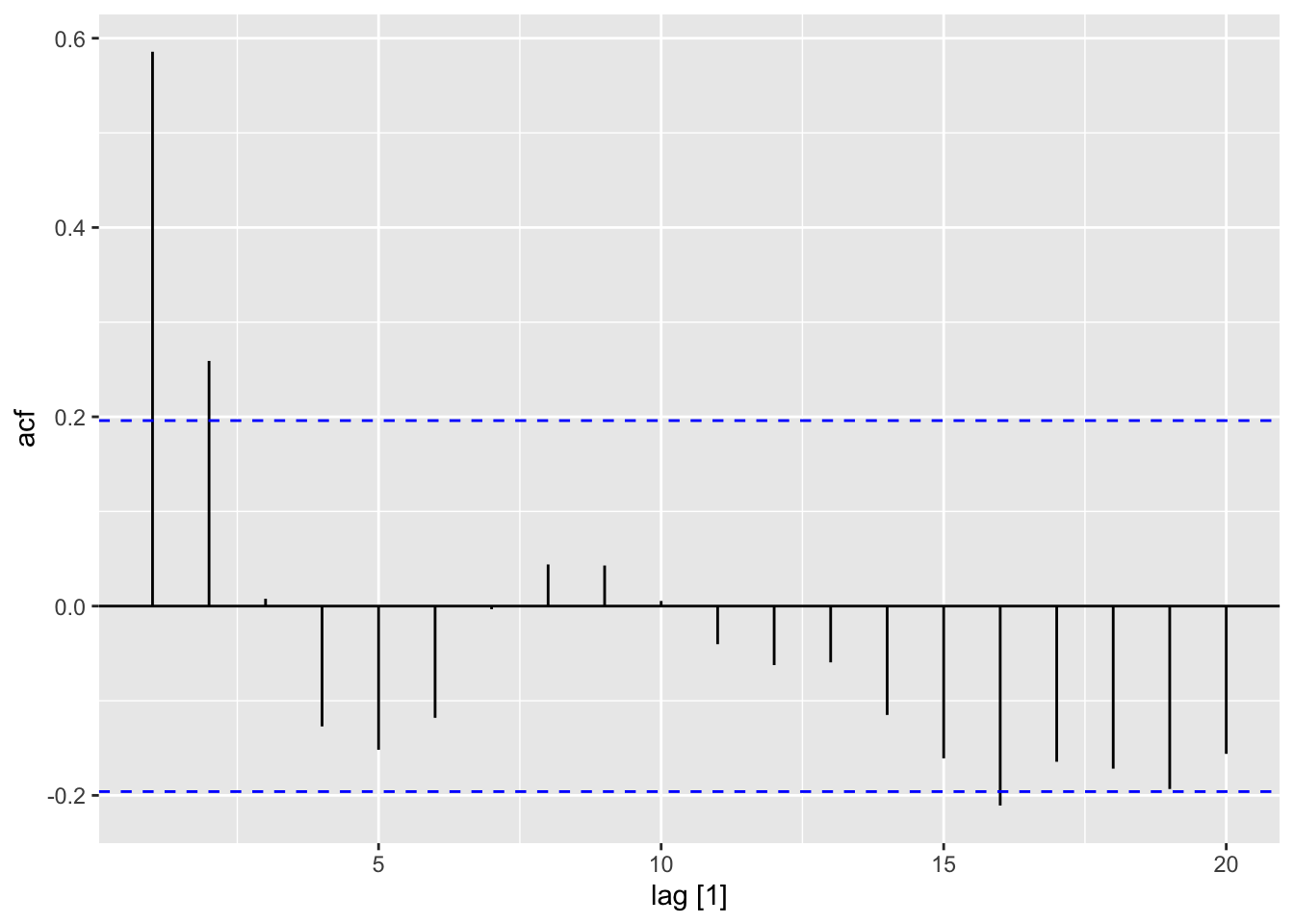

pacf(x)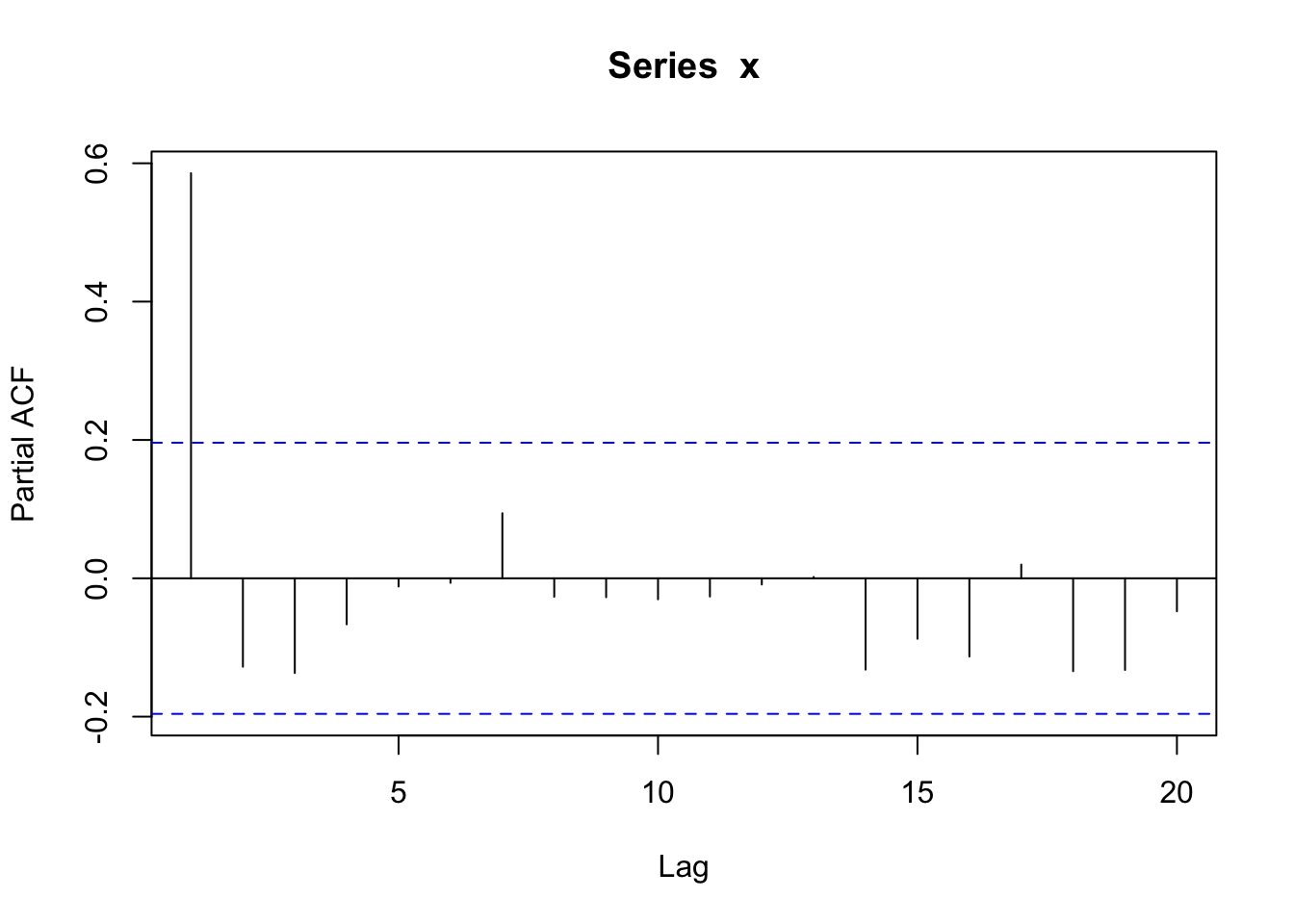

PACF(dat, x) |>
    autoplot()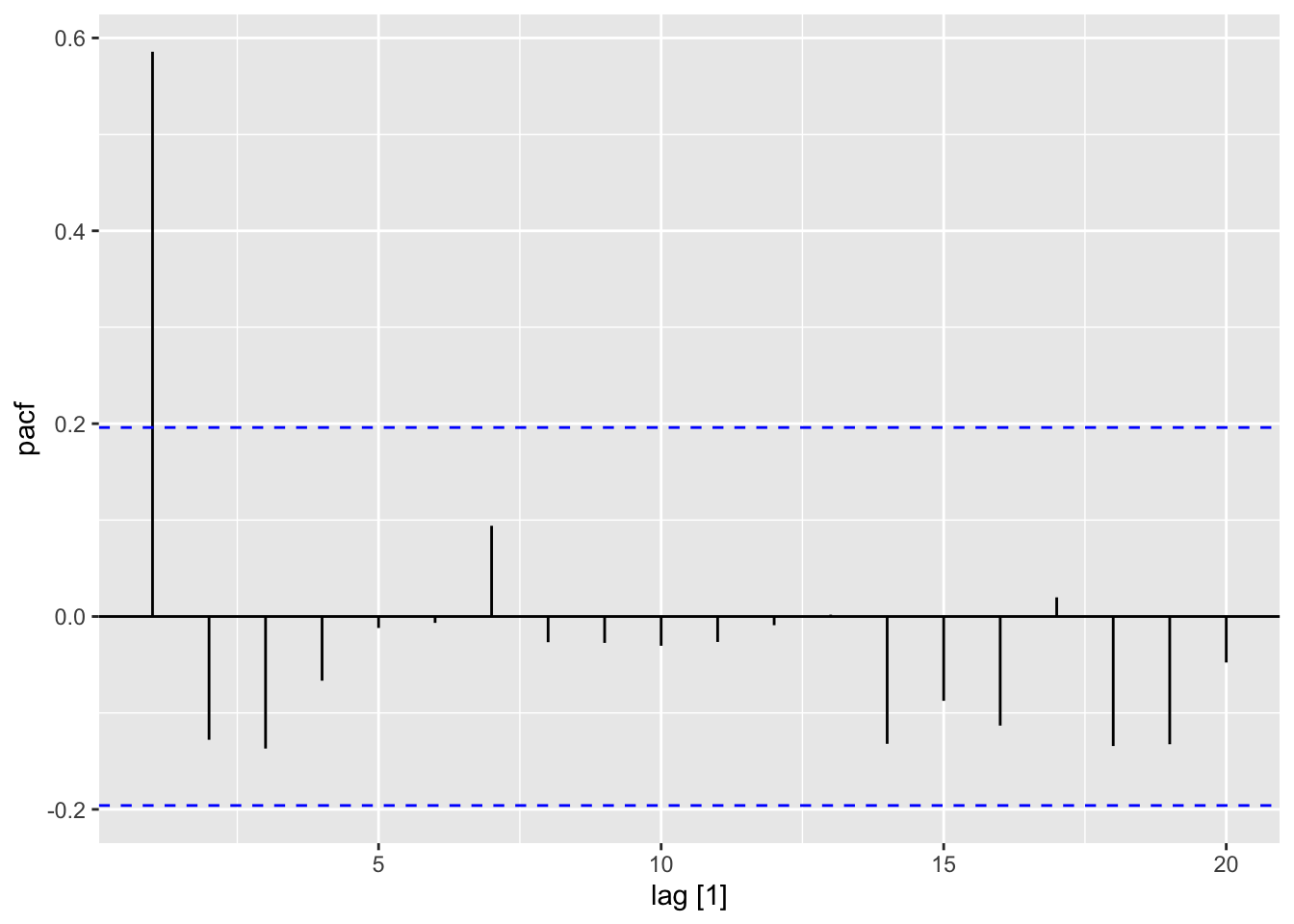

Show the Book code in full 
rho <- function(k, alpha) alpha^k
layout(1:2)
plot(0:10, rho(0:10, 0.7), type = "b")
plot(0:10, rho(0:10, -0.7), type = "b")
set.seed(1)
x <- w <- rnorm(100)
for (t in 2:100) x[t] <- 0.7 * x[t - 1] + w[t]
plot(x, type = "l")
acf(x)
pacf(x)
Show the Tidyverts code in full 
set.seed(1)
dat <- tibble(w = rnorm(100)) |>
    mutate(
        index = 1:n(),
         x = purrr::accumulate2(
            lag(w), w, 
            \(acc, nxt, w) 0.7 * acc + w,
            .init = 0)[-1]) |>
    tsibble::as_tsibble(index = index)
autoplot(dat, .var = x)

ACF(dat, x) |>
    autoplot()

PACF(dat, x) |>
    autoplot()

4.6.1 “Model fitted to simulated series” Modern look

The stats::ar() and fable::AR() appear to have different optimization routines. For example, the fable::AR() model only allows optimization using Ordinary Least Squares (OLS), and stats::ar() provides multiple options. The textbook uses method = "mle" in these examples. Other differences are also apparent. As such, the results in the remaining sections do not match exactly.

Book code

set.seed(1)
x <- w <- rnorm(100)
for (t in 2:100) x[t] <- 0.7 * x[t - 1] + w[t]
x.ar <- ar(x, method = "mle")
x.ar$order
[1] 1

Tidyverts code

set.seed(1)
dat <- tibble(w = rnorm(100)) |>
    mutate(
        index = 1:n(),
         x = purrr::accumulate2(
            lag(w), w, 
            \(acc, nxt, w) 0.7 * acc + w,
            .init = 0)[-1]) |>
    tsibble::as_tsibble(index = index)
# Note that mle is not available using ols in ARMA
# answers slightly different
fit_ar <- dat |>
    model(AR(x ~ order(1)))
print("Order defined as 1 using order")
[1] "Order defined as 1 using order"
x.ar$ar
[1] 0.6009459
tidy(fit_ar) |>
    filter(str_detect(term, "ar")) |>
    pull("estimate")
[1] 0.6015796
x.ar$ar + c(-2, 2) * sqrt(x.ar$asy.var)[1] # slight change
[1] 0.4404031 0.7614886
tidy(fit_ar) |>
    mutate(
        lb = estimate - 2 * std.error,
        ub = estimate + 2 * std.error
    )
# A tibble: 2 × 8
  .model           term     estimate std.error statistic  p.value      lb    ub
  <chr>            <chr>       <dbl>     <dbl>     <dbl>    <dbl>   <dbl> <dbl>
1 AR(x ~ order(1)) constant    0.157    0.0955      1.65 1.03e- 1 -0.0339 0.348
2 AR(x ~ order(1)) ar1         0.602    0.0814      7.39 5.03e-11  0.439  0.764
Show the Book code in full 
x.ar <- ar(x, method = "mle")
x.ar$order
x.ar$ar
x.ar$ar + c(-2, 2) * sqrt(x.ar$asy.var)[1] # slight change
Show the Tidyverts code in full 
set.seed(1)
dat <- tibble(w = rnorm(100)) |>
    mutate(
        index = 1:n(),
         x = purrr::accumulate2(
            lag(w), w, 
            \(acc, nxt, w) 0.7 * acc + w,
            .init = 0)[-1]) |>
    tsibble::as_tsibble(index = index)
# Note that mle is not available using ols in ARMA
# answers slightly different
fit_ar <- dat |>
    model(AR(x ~ order(1)))

tidy(fit_ar) |>
    filter(str_detect(term, "ar")) |>
    pull("estimate")
tidy(fit_ar) |>
    mutate(
        lb = estimate - 2 * std.error,
        ub = estimate + 2 * std.error
    )

4.6.2 “Exchange rate series: Fitted AR model”

See note about stats::ar() and fable::AR() in previous section.

Book code

Z <- read.table("data/pounds_nz.dat", header = T)
Z.ts <- ts(Z, st = 1991, fr = 4)
Z.ar <- ar(Z.ts)
mean(Z.ts)
[1] 2.823251

Tidyverts code

z <- read_table("data/pounds_nz.dat")
date_seq <- seq(
    lubridate::ymd("1991-01-01"),
    by = "3 months",
    length.out = nrow(z))
 z_ts <- z |>
    mutate(
        date = date_seq,
        quarter = tsibble::yearquarter(date)) |>
    as_tsibble(index = quarter)
z_ar <- z_ts |>
    model(AR(xrate ~ order(1)))
mean(z_ts$xrate)
[1] 2.823251
c(Z.ar$order, Z.ar$ar)
[1] 1.000000 0.890261
tidy(z_ar) |>
    filter(str_detect(term, "ar")) |>
    pull("estimate")
[1] 1.005271
Z.ar$ar + c(-2, 2) * sqrt(Z.ar$asy.var)[1]
[1] 0.7405097 1.0400123
tidy(z_ar) |>
    mutate(
        lb = estimate - 2 * std.error,
        ub = estimate + 2 * std.error
    )
# A tibble: 1 × 8
  .model               term  estimate std.error statistic  p.value    lb    ub
  <chr>                <chr>    <dbl>     <dbl>     <dbl>    <dbl> <dbl> <dbl>
1 AR(xrate ~ order(1)) ar1       1.01   0.00781      129. 8.55e-52 0.990  1.02
acf(Z.ar$res[-1])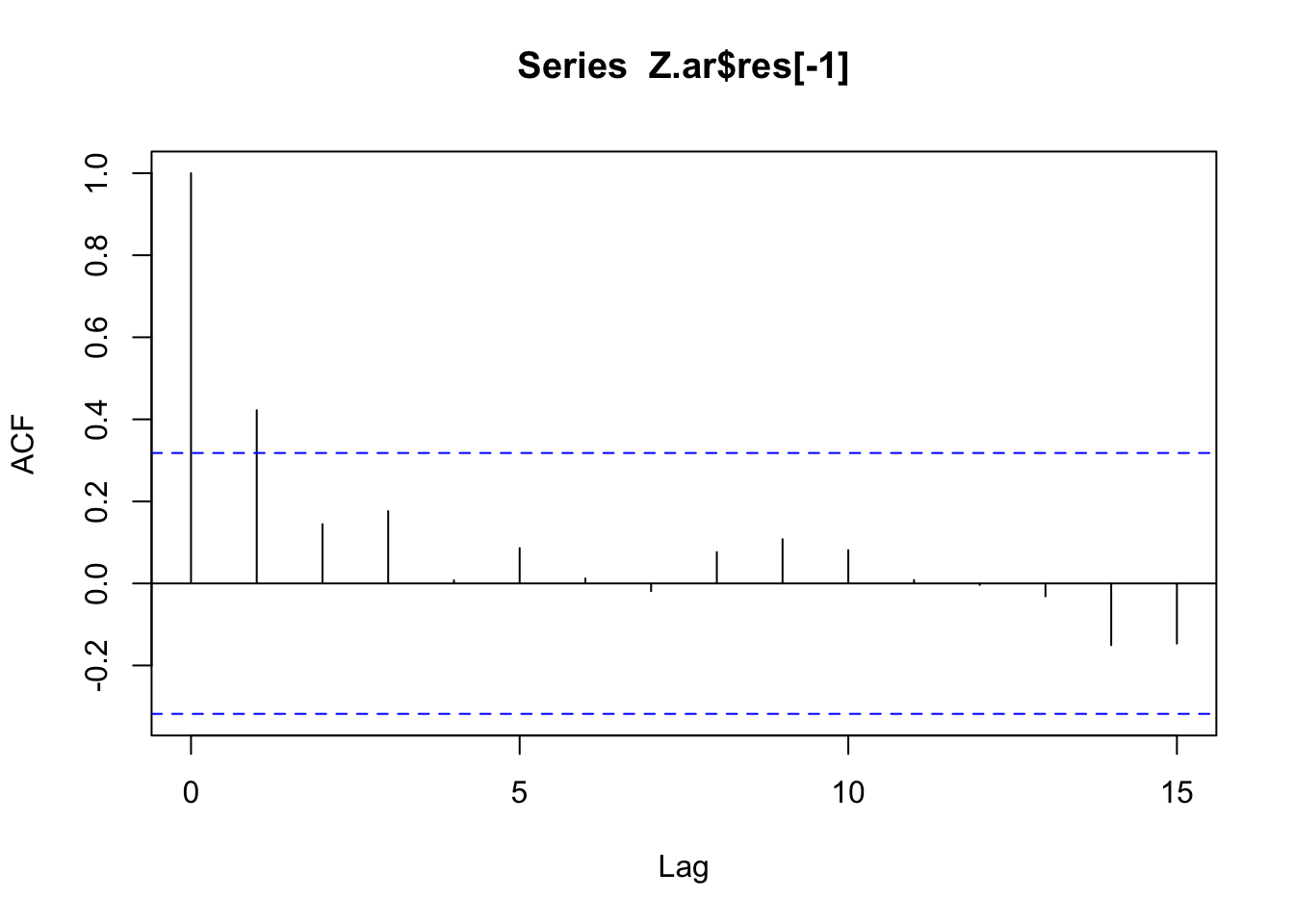

residuals(z_ar) |> ACF(y = .resid) |> autoplot()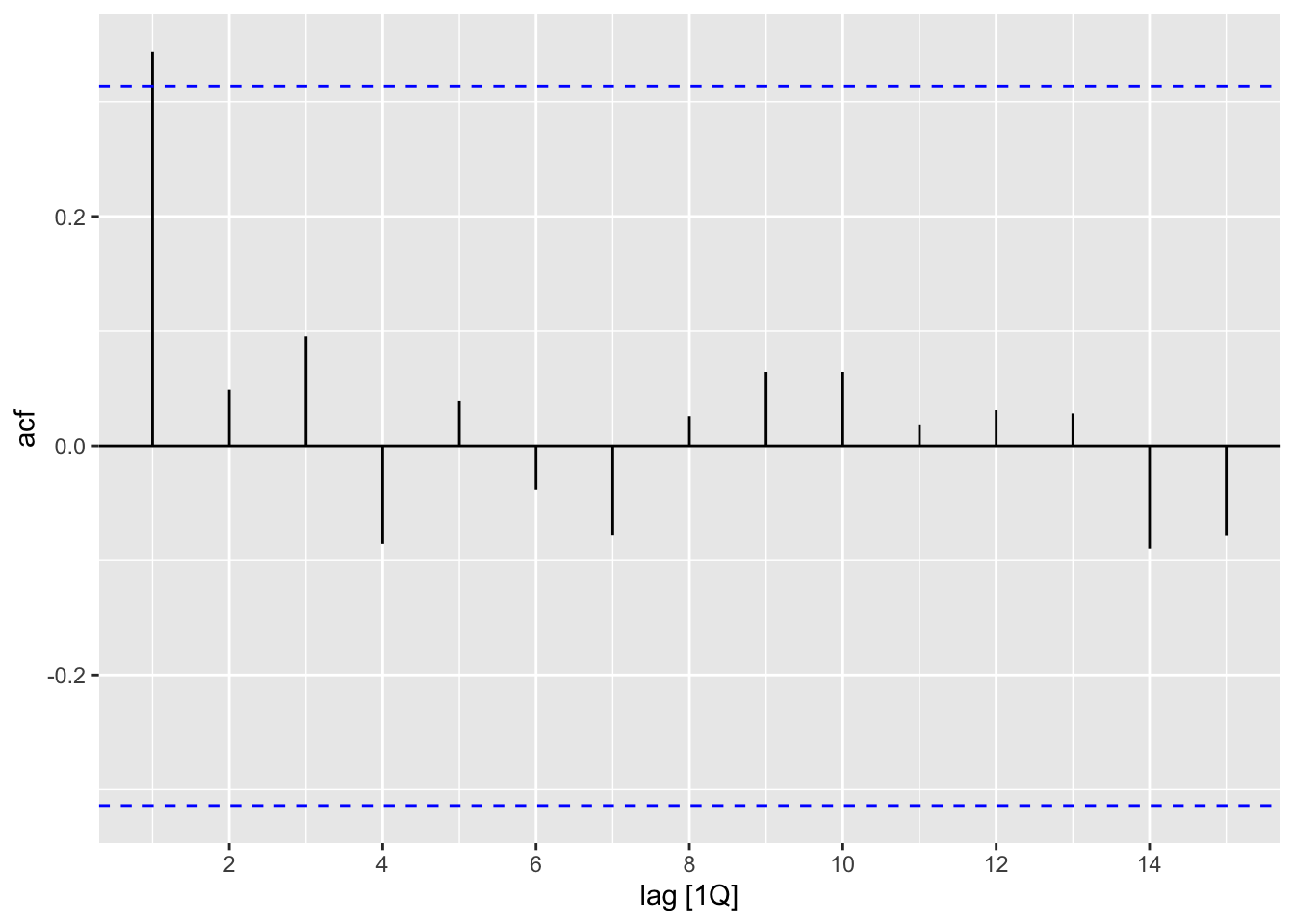

Show the Book code in full 
Z.ar <- ar(Z.ts)
mean(Z.ts)
Z.ar$order
Z.ar$ar
Z.ar$ar + c(-2, 2) * sqrt(Z.ar$asy.var)[1]
acf(Z.ar$res[-1])
Show the Tidyverts code in full 
z <- read_table("data/pounds_nz.dat")
date_seq <- seq(
    lubridate::ymd("1991-01-01"),
    by = "3 months",
    length.out = nrow(z))
 z_ts <- z |>
    mutate(
        date = date_seq,
        quarter = tsibble::yearquarter(date)) |>
    as_tsibble(index = quarter)
z_ar <- z_ts |>
    model(AR(xrate ~ order(1)))
mean(z_ts$xrate)

tidy(z_ar) |>
    filter(str_detect(term, "ar")) |>
    pull("estimate")

tidy(z_ar) |>
    mutate(
        lb = estimate - 2 * std.error,
        ub = estimate + 2 * std.error
    )

residuals(z_ar) |> ACF(y = .resid) |> autoplot()

4.6.3 “Global temperature series: Fitted AR model” Modern look

See note about stats::ar() and fable::AR() in previous section.

Book code

Global = scan("data/global.dat")
Global.ts = ts(Global, st = c(1856, 1), end = c(2005, 12),fr = 12)
Global.ar <- ar(aggregate(Global.ts, FUN = mean), method = "mle")
mean(aggregate(Global.ts, FUN = mean))
[1] -0.1382628

Tidyverts code

global <- tibble(x = scan("data/global.dat")) |>
    mutate(
        date = seq(
            ymd("1856-01-01"),
            by = "1 months",
            length.out = n()),
        year = year(date),
        year_month = tsibble::yearmonth(date))

global_ts <- global |>
    as_tsibble(index = year_month)

global_ts_year <- global |>
    summarise(x = mean(x), .by = year) |>
    as_tsibble(index = year)

global_ar <- global_ts_year |>
    model(AR(x ~ order(1:9)))

mean(global_ts$x)
[1] -0.1382628
Global.ar$order
[1] 4
tidy(global_ar) |> filter(str_detect(term, "ar")) |> nrow()
[1] 4
Global.ar$ar
[1] 0.58762026 0.01260252 0.11116731 0.26763656
tidy(global_ar) |> filter(str_detect(term, "ar")) |> pull(estimate)
[1] 0.58176066 0.02164876 0.10747306 0.26707158
acf(Global.ar$res[-(1:Global.ar$order)], lag = 50)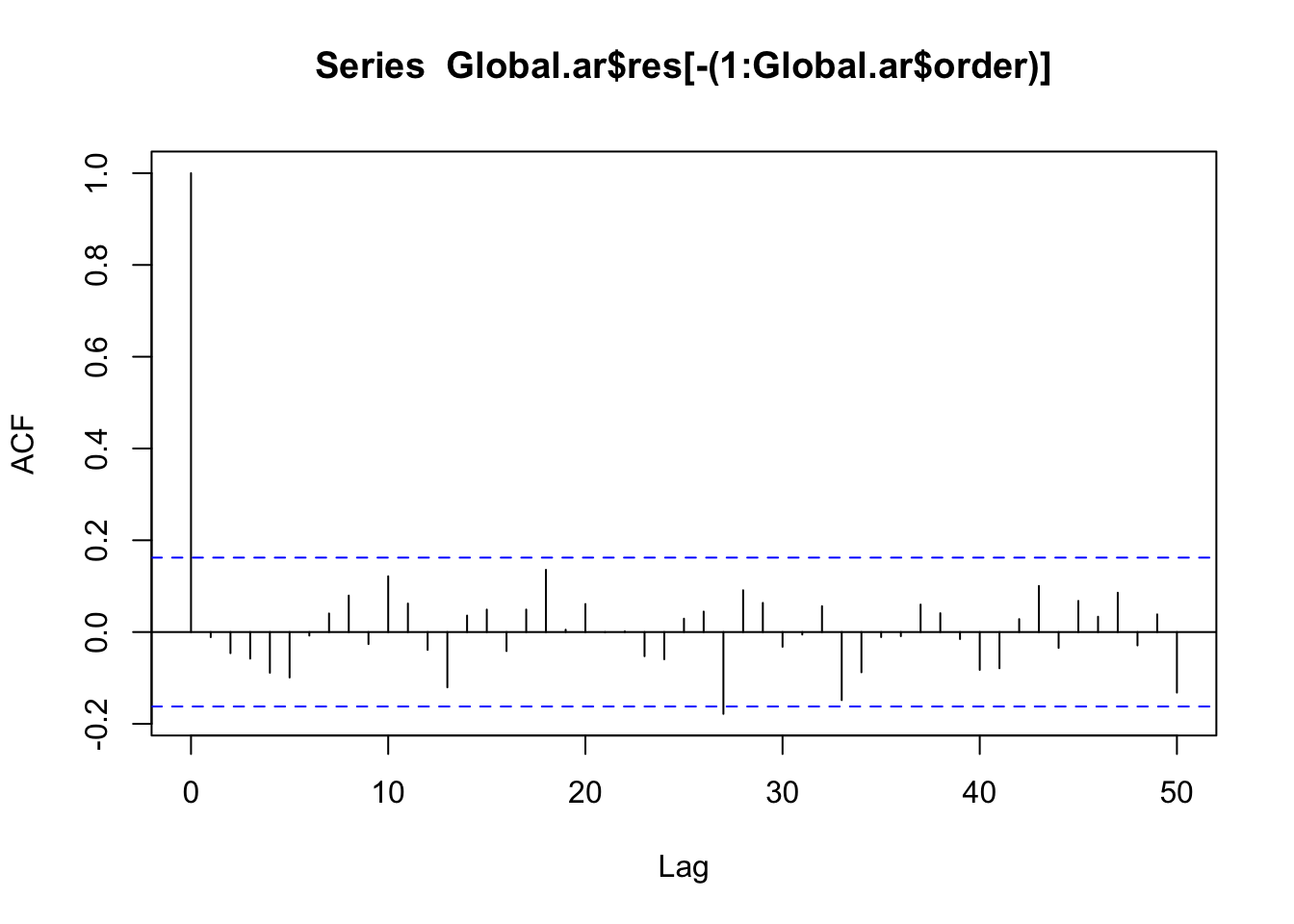

residuals(global_ar) |> ACF(lag_max = 50) |> autoplot()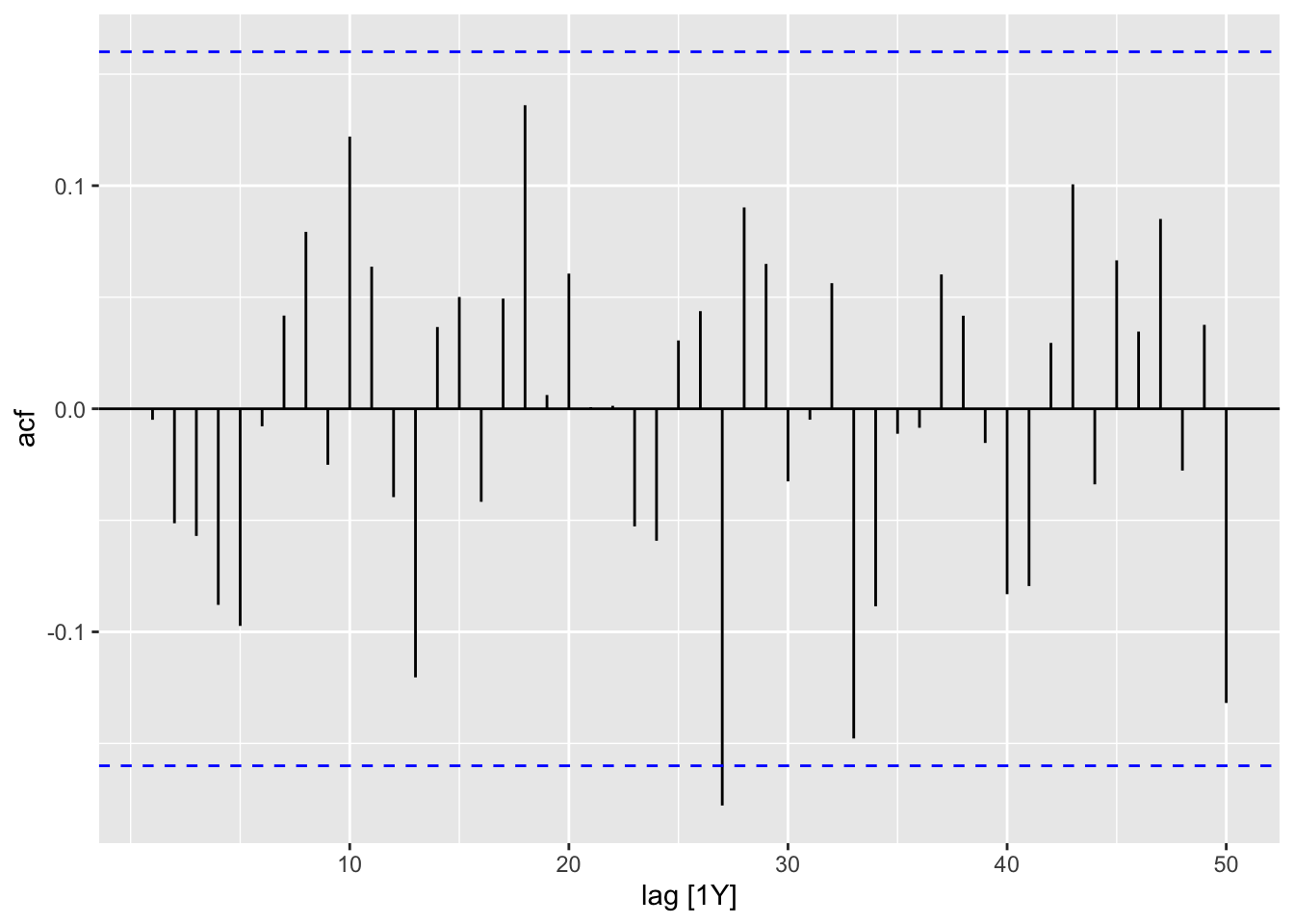

Show the Book code in full 
Global = scan("data/global.dat")
Global.ts = ts(Global, st = c(1856, 1), end = c(2005, 12),fr = 12)
Global.ar <- ar(aggregate(Global.ts, FUN = mean), method = "mle")
mean(aggregate(Global.ts, FUN = mean))
Global.ar$order
Global.ar$ar
acf(Global.ar$res[-(1:Global.ar$order)], lag = 50)
Show the Tidyverts code in full 
global <- tibble(x = scan("data/global.dat")) |>
    mutate(
        date = seq(
            ymd("1856-01-01"),
            by = "1 months",
            length.out = n()),
        year = year(date),
        year_month = tsibble::yearmonth(date))

global_ts <- global |>
    as_tsibble(index = year_month)

global_ts_year <- global |>
    summarise(x = mean(x), .by = year) |>
    as_tsibble(index = year)

global_ar <- global_ts_year |>
    model(AR(x ~ order(1:9)))

mean(global_ts$x)

tidy(global_ar) |> filter(str_detect(term, "ar")) |> nrow()

tidy(global_ar) |> filter(str_detect(term, "ar")) |> pull(estimate)

residuals(global_ar) |> ACF(lag_max = 50) |> autoplot()

4.7 Summary of Modern R commands used in examples