Permutation Tests
A nonparametric approach to computing the p-value for any test statistic in just about any scenario.
Overview
In almost all hypothesis testing scenarios, the null hypothesis can be interpreted as follows.
\(H_0\): Any pattern that has been witnessed in the sampled data is simply due to random chance.
Permutation Tests depend completely on this single idea. If all patterns in the data really are simply due to random chance, then the null hypothesis is true. Further, random re-samples of the data should show similar lack of patterns. However, if the pattern in the data is real, then random re-samples of the data will show very different patterns from the original.
Consider the following image. In that image, the toy blocks on the left show a clear pattern or structure. They are nicely organized into colored piles. This suggests a real pattern that is not random. Someone certainly organized those blocks into that pattern. The blocks didn’t land that way by random chance. On the other hand, the pile of toy blocks shown on the right is certainly a random pattern. This is a pattern that would result if the toy blocks were put into a bag, shaken up, and dumped out. This is the idea of the permutation test. If there is structure in the data, then “mixing up the data and dumping it out again” will show very different patterns from the original. However, if the data was just random to begin with, then we would see a similar pattern by “mixing up the data and dumping it out again.”

The process of a permutation test is:
- Compute a test statistic for the original data.
- Re-sample the data (“shake it up and dump it out”) thousands of times, computing a new test statistic each time, to create a sampling distribution of the test statistic.
- Compute the p-value of the permutation test as the percentage of test statistics that are as extreme or more extreme than the one originally observed.
In review, the sampling distribution is created by permuting (randomly rearranging) the data thousands of times and calculating a test statistic on each permuted version of the data. A histogram of the test statistics then provides the sampling distribution of the test statistic needed to compute the p-value of the original test statistic.
Explanation
The most difficult part of a permutation test is in the random permuting of the data. How the permuting is performed depends on the type of hypothesis test being performed. It is important to remember that the permutation test only changes the way the p-value is calculated. Everything else about the original test is unchanged when switching to a permutation test.
Independent Samples t Test
For the independent sample t Test, we will use the data from the independent
sleep analysis. In that analysis, we were using the
sleep data to test the hypotheses:
\[ H_0: \mu_\text{Extra Hours of Sleep with Drug 1} - \mu_\text{Extra Hours of Sleep with Drug 2} = 0 \] \[ H_a: \mu_\text{Extra Hours of Sleep with Drug 1} - \mu_\text{Extra Hours of Sleep with Drug 2} \neq 0 \]
We used a significance level of \(\alpha = 0.05\) and obtained a P-value of \(0.07939\). Let’s demonstrate how a permutation test could be used to obtain this same p-value. (Technically you only need to use a permutation test when the requirements of the original test were not satisfied. However, it is also reasonable to perform a permutation test anytime you want. No requirements need to be checked when performing a permutation test.)
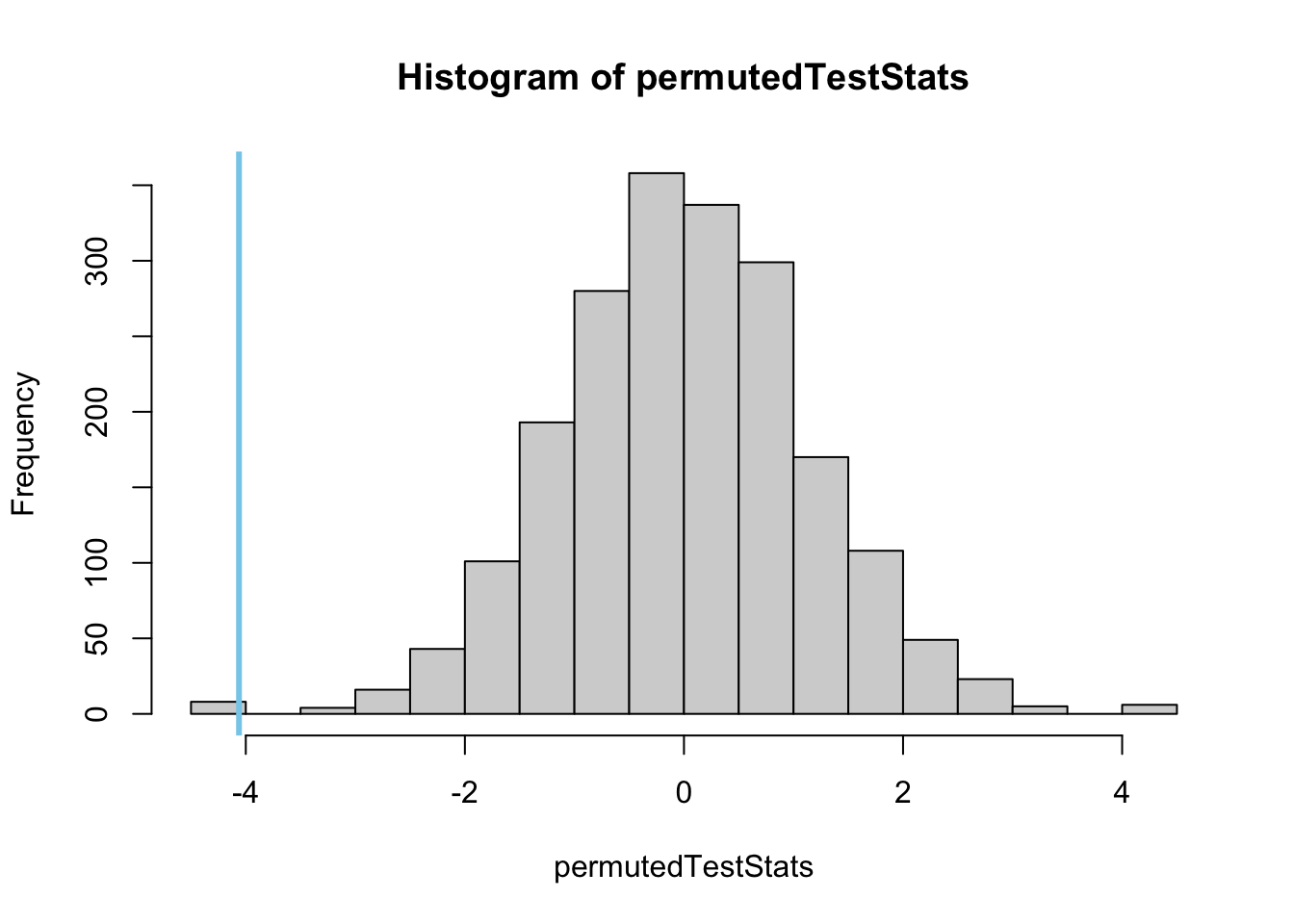
# First run the initial test and gain the test statistic:
myTest <- t.test(extra ~ group, data = sleep, mu = 0)
observedTestStat <- myTest$statistic
# Now we run the permutations to create a distribution of test statistics
N <- 2000
permutedTestStats <- rep(NA, N)
for (i in 1:N){
permutedTest <- t.test(sample(extra) ~ group, data = sleep, mu = 0)
permutedTestStats[i] <- permutedTest$statistic
}
# Now we show a histogram of that distribution
hist(permutedTestStats, col = "skyblue")
abline(v = observedTestStat, col = "red", lwd = 3)
#Greater-Than p-value: Not the correct one in this case
sum(permutedTestStats >= observedTestStat)/N
# Less-Than p-value: Not the correct one for this data
sum(permutedTestStats <= observedTestStat)/N
# Two-Sided p-value: This is the one we want based on our alternative hypothesis.
2*sum(permutedTestStats <= observedTestStat)/NNote The Wilcoxon Rank Sum test is run using the
same code except with
myTest <- wilcox.test(y ~ x, data=...) instead of
t.test(...) in both Step’s 1 and 2.