Project Outline

This project outline and background information will assist you as you complete your project. You should assume the reader of your work has no knowledge or access to this information, which means you’ll need to incorporate portions of this introduction into your work, as they seem relevant.

How long does an LED light bulb last? Lumens are a measure of how much light you get from a bulb. When you first turn on an LED bulb, the lumen output slightly increases for a while, going above the initial brightness. While LEDs do not “burn out”, after peaking the lumen output stays relatively constant before it starts to decrease. In the bulb data we will use, lumen measures are normalized to the initial intensity of the bulb, so that we can compare different bulbs.

In 2008, the US Department of Energy launched the Bright Tomorrow Lighting Prize (or L Prize) to encourage the development of high-efficiency replacement for the incandescent light bulb. To win the prize the bulb needed a lifetime longer than 25,000 hours (almost 3 years). Source

We do not have three years of data on our bulbs, rather we will use mathematical models to predict bulb lifetimes. Our work in this project relies on assumed mathematical models. We will

use R to plot provided data,
explore how parameters change the behavior of several functions we will be using as models,
visually fit several deterministic models to data, and
use the fitted models to provide information about how long an LED bulb lasts.

In this project, we’ll be fitting the data to deterministic models, functions $f(t)$, that give the lumen output of LED bulbs (as a percent of the initial lumens) after $t$ hours. The input of the models is time, $t$, measured in hours since the bulb is turn on. The output of the models is bulb intensity, $f(t)$, measured as a percent of initial bulb intensity. By choosing to normalize bulb intensity in this way, we have fixed the initial output as 100% of the original intensity, which means $f(0) = 100$. For this project, we will use 80% of the initial intensity¹ as the threshold for determining the lifetime of a light bulb. This means that once the bulb intensity decreases below 80%, we will consider this the life of the bulb (in other words the bulb “burned out”).

Task 1: Background and Data

Create an R Markdown file.

Use the led_bulb() function to store data for a single bulb in the variable bulb, using your assigned seed from I-Learn. You will need to install the devtools and byuidatascience/data4led packages. The code below can help you accomplish this.

#Uncomment and run the line below once in the console to get the devtools package.
  #install.packages("devtools")

#Uncomment and run the line below once in the console to get the data4led package.
  #devtools::install_github("byuidatascience/data4led") 

#Use the code below to load the data4led package to your current R session.
library(data4led)

#After entering the seed from the class list of seeds, use the code below to load the data for one randomly selected bulb. 
bulb <- led_bulb(1,seed = DDDD)
#Setting the seed fixes which randomly selected bulb you will use.
#This makes your work reproducible.

This code creates a data frame called “bulb”. The bulb data frame contains measurements for one randomly selected bulb at many time points. You will need to set the seed so that you will have your own random, but reproducible, data with which to work. Please set the seed as the four digit number from the class list of assigned seeds.

Use head(bulb) to view the first 6 lines of the bulb data frame you created. Verify that this data frame, a table, includes the columns
1. “id”, the identification number for your randomly selected bulb,
2. “hours”, the number of hours since the bulb has turned on,
3. “intensity”, the lumen output of the bulb,
4. “normalized_intensity”, the lumen at that time divided by the lumen of your bulb at time 0, and
5. “percent_intensity”, the bulb intenstity as a percent of the original lumen (notice the first row in this column is 100).
Use the plot() command in R, along with the bulb data frame, to create a time vs. bulb intensity (as a percent of the original lumens) scatter plot for the one light bulb corresponding to your seed. Make sure hours is on the horizontal axis ($x$-axis) and percent_intensity is on the vertical axis ($y$-axis).
- CHECK YOUR WORK: Do you get a plot with 44 points? Is the horizontal axis from 0 to about 5000? Is the point $(0,100)$ on your plot?
- CHECK YOUR WORK: Use this Shiny App to check your work.
Organize your work into a cohesive analysis and submit the html file on Canvas.

You’ll see the instructions “Organize your work into a cohesive analysis” at the end of every task. Imagine that you are submitting a report to a boss. Your work needs to be readable. Your job is to analyze the task at hand for your boss.

Task 2: Models and Parameter Exploration

Create a new R Markdown file.
Consider the following six general models.
- $f_0(x; a_0) = a_0$ where $x \geq 0$
- $f_1(x; a_0,a_1) = a_0 + a_1x$ where $x \geq 0$
- $f_2(x; a_0,a_1,a_2) = a_0 + a_1x + a_2x^2$ where $x \geq 0$
- $f_3(x; a_0,a_1,a_2 ) = a_0 + a_1e^{-a_2x}$ where $x \geq 0$
- $f_4(x; a_0,a_1,a_2) = a_0 + a_1x + a_2\ln(0.005x+1)$ where $x \geq 0$
- $f_5(x; a_0,a_1,a_2) = (a_0+a_1x)e^{-a_2x}$ where $x \geq 0$
For each function, use the sliders in the Desmos files below to dynamically explore how changing the parameter changes the behavior of the function.
For each function, in your personal notes, observe how changing the parameters changes the behavior of the function (or model). Try to summarize your observations in terms of transformations of functions (shifts, reflections, stretch) and the mathematical behavior of the function (increasing, decreasing, constant, positive, negative, nonnegative). For each function, in your personal notes, identify interesting parameter values (or ranges of values) that highlight different representative behaviors.
From the functions $f_3$, $f_4$, and $f_5$, pick two functions to describe. You only need to include two functions in your cohesive analysis for this task. In your cohesive analysis, summarize your observations about the parameters ($a_0$, $a_1$ and $a_2$) in terms of transformations of functions (shifts, reflections, stretch) and the mathematical behavior of the functions (increasing, decreasing, constant, positive, negative, nonnegative). For the two functions you selected, use the plot() commands in R to plot at least two representative curves illustrating what you learned in your parameter exploration. Use the par(mfrow()) command to organize your plots into one figure.
- CHECK YOUR WORK: For each function you selected does your code produce at least 2 plots in the same figure that show curves with different representative behaviors? There is no Shiny App for this Task.
Organize your work into a cohesive analysis and submit the html file on Canvas.
- Remember to clearly specify, in your narrative (not just the code chunks), the parameter values you use in each plot. This is required to make your work is reproducible.
- As needed, review the explanation of a cohesive analysis, found at the end of Task 1 and in the project specs details.

Task 3: Fit the Models (“Visual” Method)

Create a new R Markdown file.
Consider the following general models.
- $f_0(t; a_0) = a_0$ where $t \geq 0$
- $f_1(t; a_0,a_1) = a_0 + a_1t$ where $t \geq 0$
- $f_2(t; a_0,a_1,a_2) = a_0 + a_1t + a_2t^2$ where $t \geq 0$
- $f_3(t; a_0,a_1,a_2 ) = a_0 + a_1e^{-a_2t}$ where $t \geq 0$
- $f_4(t; a_0,a_1,a_2) = a_0 + a_1t + a_2\ln(0.005t+1)$ where $t \geq 0$
- $f_5(t; a_0,a_1,a_2) = (a_0+a_1t)e^{-a_2t}$ where $t \geq 0$
Use that fact that the percent of orignial lumens at $t=0$ is 100% to determine $a_0$ for each function. Examples showing how to do this for $f_0$, $f_2$, and $f_5$ have been done for you.
- Since $f_0(0)$ must be 100, we know $a_0 = 100$. The fitted model $f_0$ is $f_0(t) = 100$ where $t \geq 0$.
- Since $f_2(0) = 100$, we know $f_2(0) = a_0 + a_1(0) + a_2(0^2) = a_0 + 0 + 0 = a_0$ so $a_0 = 100$.
- Since $f_5(0) = 100$, we know $f_5(0) = (a_0 + a_1(0))e^{-a_2(0)} = (a_0 + 0)(1) = a_0$ so $a_0 = 100$.
CAUTION: The parameter $a_0$ is not always equal to 100.
- Given $f_1(0) = 100$, find $a_0$.
- Given $f_3(0) = 100$, find $a_0$. Note: $a_0 \neq 100$.
- Given $f_4(0) = 100$, find $a_0$.
For all six model, $f_i(t)$, select parameter values to give a visual fit of the model to the data. Make sure to pick parameters so that $f_i(0) = 100$.
- In your cohesive analysis, clearly state your six fitted models with the chosen parameters (not just in the code chunks). This helps makes your work reproducible.
- See the following links for some help getting started finding the visual fits. There is a video, showing an example of fitting $f_2$ when the seed is 2021, and a few accompanying html files.
  - Video: Visually Fitting $f_2$ Example
Use the plot() and lines() commands in R to plot each of your fitted models on top of the scatter plot of the data (there is an example below of how to do this for $f_0$). For model, construct two plots of the model and data, the first with a “zoomed in” window (defined by the values in the data) so you can see the fit of the model to the data, and the second with a “zoomed out” window using xlim = c(0,80000) and ylim = c(-10,120) so that you can see the story the function tells. Use mfrow=c(1,2) to place these plots side-by-side in the same figure. You should have 6 figures, each with two plots.
- CHECK YOUR WORK: When you evaluate your fitted function at 0, do you get 100? When you plot your function is it a good fit to the data (look at the “zoomed in” window)?
- CHECK YOUR WORK: Use this Shiny App to check your work.
Describe in 1-3 sentences the story told by each of the fitted functions, regardless of how preposterous (tell the story).
- For example the following code plots the “zoomed in” and “zoomed out” plots of $f_0$ with the data. For the purposes of this example we will use the seed 2021, you should use your seed from the class list of assigned seeds.
  
  Below is a plot of the fitted function $f_0(t) = 100$ with $t \geq 0$. This function is a horizontal line at 100% intensity.
```
library(data4led)
bulb <- led_bulb(1,seed = 2021)

t <- bulb$hours
y1 <- bulb$percent_intensity

f0 <- function(x,a0=1){a0 + 0*x}
x <- seq(0,100000,5)
y2 <- f0(x,a0=100)

par(mfrow=c(1,2),mar=c(2.5,2.5,1,0.25))
plot(t,y1,xlab="Hour", ylab="Intensity(%) ", pch=16)
lines(x,y2,col=2)
plot(t,y1,xlab="Hour", ylab="Intensity(%) ", pch=16, xlim = c(0,80000),ylim = c(-10,120))
lines(x,y2,col=2)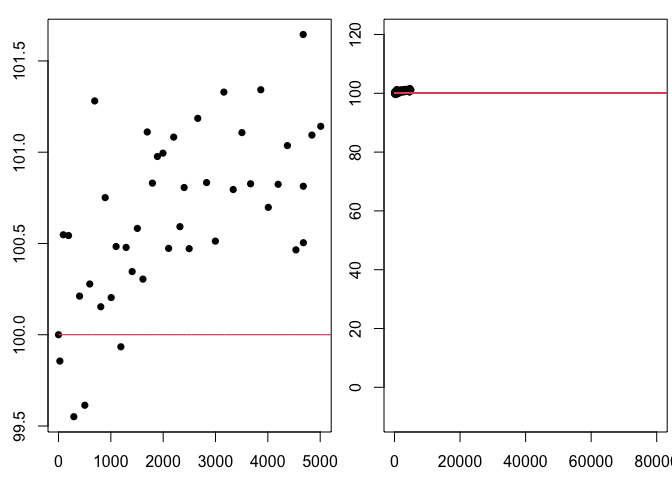
```
  This fitted model says the light bulb will stay on at its original intensity for all time, beginning when it is turned on. When we evaluate the fitted $f_0(t) = 100$ at $t=0$, we see below, $f_0(0) = 100$ as required by the normalization.
```
f0(0,a0=100)
```
```
## [1] 100
```
Organize your work into a cohesive analysis and submit the html file on Canvas.
- As needed, review the explanation of a cohesive analysis, found at the end of Task 1 and in the project specs details.

Task 4: Use the Fitted Models to Answer Questions

Create a new R Markdown file.
Find the exact solution, if possible, for where each of your six fitted models is at 80% of the initial intensity.
- This means solve the following equations $f_0(t) = 80$, $f_1(t) = 80$, $f_2(t) = 80$, $f_3(t) = 80$, $f_4(t) = 80$, and $f_5(t) = 80$ where $f_0$, $f_1$, $f_2$, $f_3$, $f_4$, and $f_5$ are your fitted functions.
- Write out your solutions and include a picture of each of your calculations (or you can use the Latex Cheat Sheet if you would like to try to type out your calculations).
- Remember to clearly specify, in your narrative (not just the calculation), the parameter values for each fitted model (so that your work is reproducible).
Use the uniroot() function in R to find the approximate solution for where each of your six fitted models is at 80% of the initial intensity, $f_i(t) = 80$.
- CHECK YOUR WORK: Compare your exact answers (found by hand) to your approximate answers (found using uniroot()). Make sure they match.
- CHECK YOUR WORK: Use this Shiny App, to check your work.
  - In your analysis include an image for each function from Shiny App to show that the solutions found (or not found) are correct.
Are any of your fitted models inconsistent with the information we know about the behavior of LED bulbs? State which, if any, of your fitted models are inconsistent with the information given about the behavior of LED bulbs (provided in the introductory information above).
- If a fitted model is inconsistent with known truth about a situation, it should not be used as a model in that situation.
Organize your work into a cohesive analysis and submit the html file on Canvas.

Project 1: Bringing it All Together (and answer a question)

Create a new R Markdown file.
Answer the question, “How long does an LED light bulb last?”
- Begin with background and an introduction to the question(s) you will be answering with the light bulb data.
- Introduce the given data.
- Introduce the six general models.
- Describe how you will fit the models (maybe what it means to fit those models).
- Provide the fitted models.
- Describe interesting stories the fitted models tell, how the stories are different, if any of the stories inconsistent with known models, which models should be ignored moving forward and why, what information you find from the fitted models, how that information depends on assumptions, etc.
  - If a fitted model is inconsistent with known truth about a situation, it should not be used as a model in that situation. Are any of your fitted models inconsistent with the information we know about the behavior of LED bulbs (provided in the introductory information of this project)?
- State the answer(s) to the question obtained from the fitted models consistent with the data.
Describe in 4-6 sentences how the information you get from the data depends on the general model you assume. Why is this an important concept to understand when working with models and data?
Organize your work into a cohesive analysis.
- Your narrative should stand alone, so apart from the “project instructions” (meaning your reader should not need the instructions for the project to understand what you are doing or explaining) and separate from the individual Tasks (meaning you should not assume your reader has read any of your previous narratives).
- It is your job in the narrative to lead your reader from the background and question to given data and 6 general models, fitting those models, and answering a question about the data using those fitted models.
- You’ll be using much of the work you did in previous tasks, however your job now is to organize the relevant work into a cohesive analysis that includes the relevant parts needed to answer the original question.
Reflect on your work for this project. At the bottom of your report include the following in a brief (1-2 paragraph) reflection.
- Identify/explain 2-3 key mathematical ideas you learned (and would like to remember).
- Identify/explain 1-3 soft skills you needed/improved/learned while working on the project.
  - List of some Soft Skills
    - Dedication
    - Following Directions
    - Motivation
    - Self-directed
    - Organization
    - Planning
    - Time Management
    - Willing to Accept Feedback
    - Perseverance
    - Good attitude
    - Meets deadlines
    - Willingness to learn
Sumbit your report to Canvas.

This number is a simplified story for illustrative purposes only.↩︎

Project 1 Instructions